3.4.6 HMOTNOST A ENERGIE
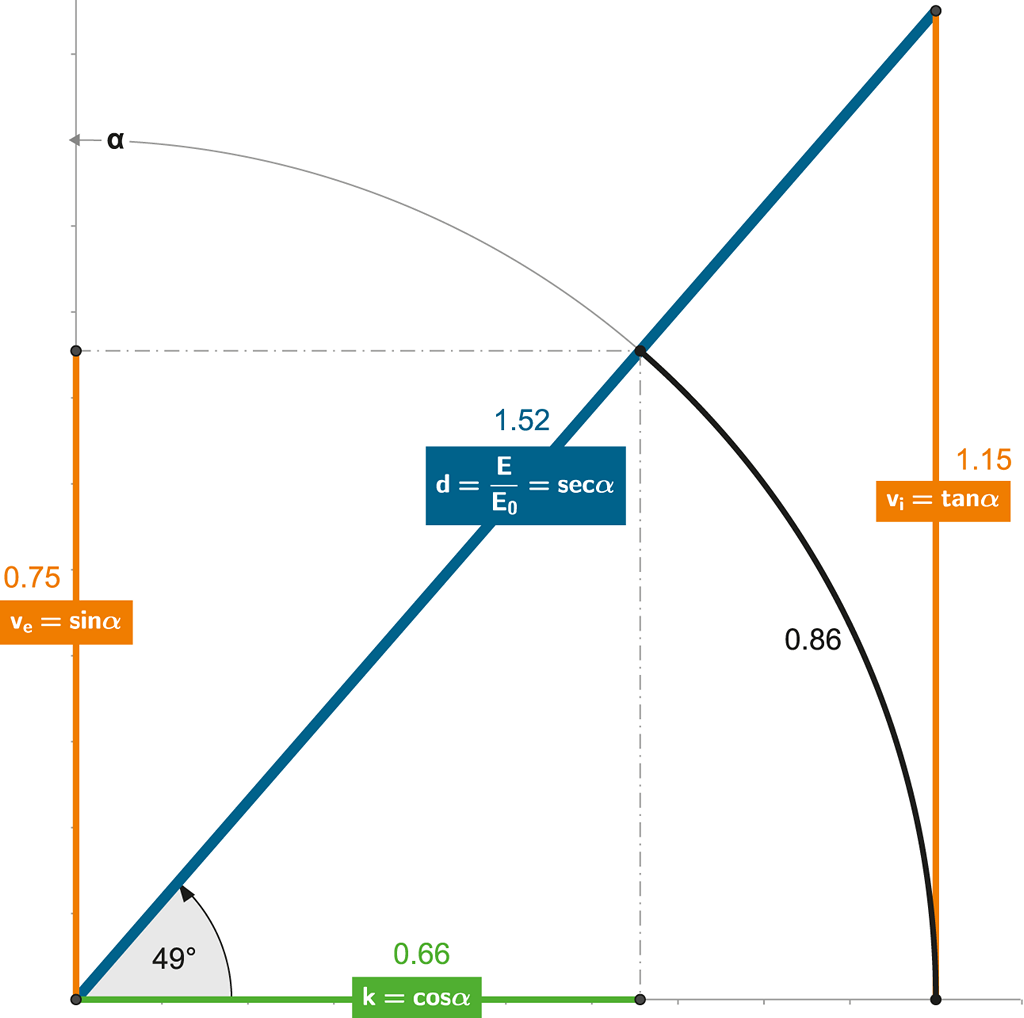
Obrázek 110:
Nově nám sekanta definuje i nárůst celkové energie (hmotnosti), v důsledku přírůstku energie kinetické.
Sekanta časoprostorového úhlu definuje též poměrný nárůst celkové energie (E), a to vůči primární energii objektu (E0). Pohyb objektu si vždy žádá kinetickou energii, a v důsledku tak musí celková energie (hmnotnost) objektu růst. Právě tento poměr vyjadřuje funkce secans!
Zde narážíme na velmi zajímavý fenomén:
Energie (hmota, hmotnost) pohybujícího se objektu roste s rychlostí stejnou měrou, jakou roste dilatace času E/E0 = d = te/ti.
Obojí popisuje sekanta úhlu (vždy větší či rovna jedné).
Co to znamená?
Že nám uniká něco velmi podstatného!
Kategorie „čas“ a „energie“ vnámíme ve fyzice velmi rozdílně. Zatímco jsme se stěží vyrovnali s fenoménem dilatace/kontrakce času (pohyb ovlivňuje tok času), staví před nás fyzika další záhadu – míra časových disporporcí (spojených s pohybem) je totožná s mírou růstu energie (hmoty) pohybujcího se objektu.
Zdá se, že 3 základní (námi odděleně chápané) kategorie pohyb, energie a čas jsou ve skutečnosti jedním fyzikálním fenoménem, jehož souvislosti nám zatím zůstávají utajeny.
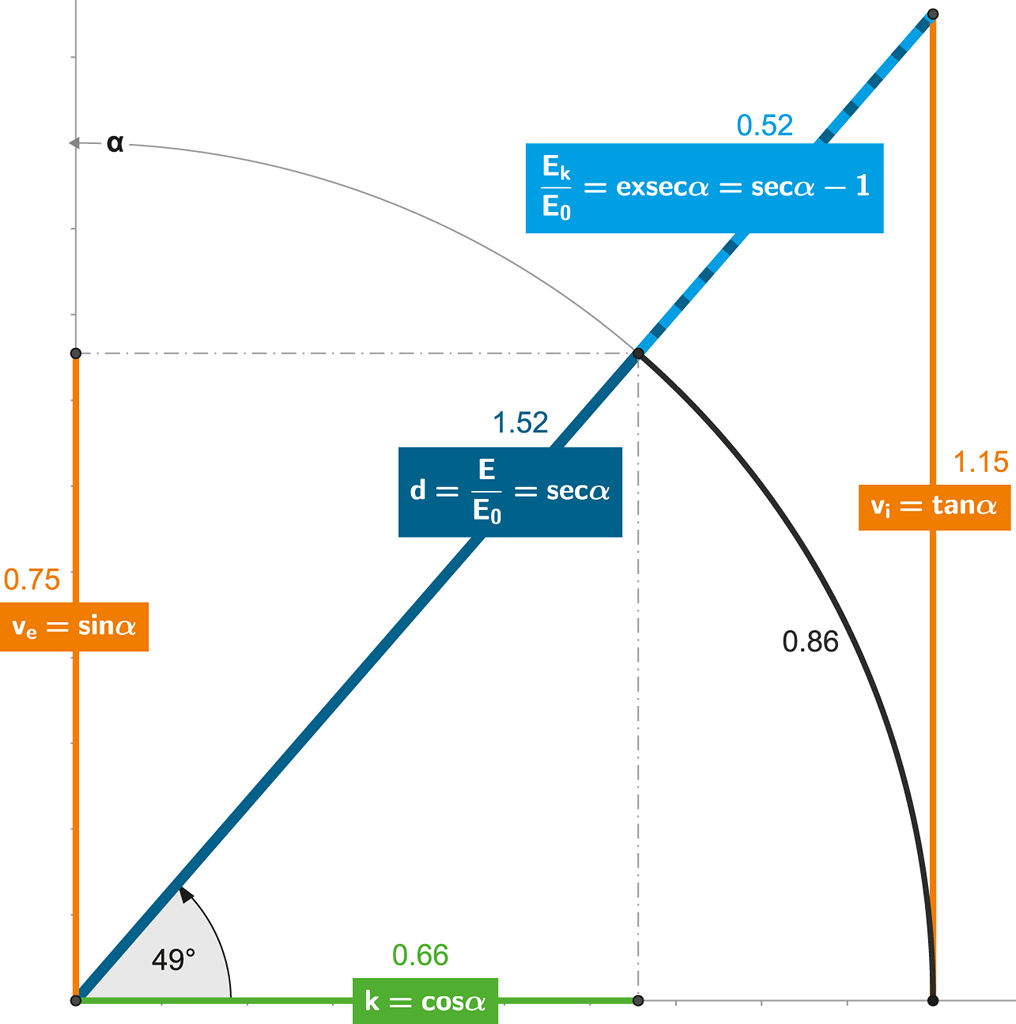
Obrázek 111:
Přírůstek kinetické energie udává „obstarožní“ funkce exsecans, což není nic jiného nežli secans ponížený o jedničku.
Odečteme-li od secans úhlu jedničku, dostáváme exsec – jehož hodnota reprezentuje poměrný přírůstek kinetické energie, respektive poměr kinetické (Ek) a primární energie (E0)! Exsecans může nabývat libovolných kladných hodnot.
Poměr nárůstu celkové energie, respektive celkové hmoty tělesa tedy vyjadřuje funkce secans E/E0 = sec α.
Secans je méně používanou funkcí, kterou na kalkulačkách běžně nenajdeme – lze ji totiž snadno dopočítat sec α = 1/cos α. Při nulovém úhlu je secans rovný jedné – což v našem případě reprezentuje fakt, že těleso o primární energii 1 kilogram má v klidu energii (respektive hmotnost) stále 1 kilogram.
S rostoucím pohybem tělesa roste i časoprostorový úhel a secans úhlu se stává větším jedné. Ke zrychlování tělesa je vždy potřeba energie (a každá energie má svoji hmotnost). Rostoucí secans úhlu tak přímo udává poměr nárůstu celkové energie pohybujícího se objektu.
Přírůstek této energie vzhledem k primární energii vypočítáme snadno:
Odečteme-li od secans úhlu jedničku, dostáváme tak hodnotu přírůstku kinetické energie. K tomuto účelu existuje speciální trigonometrická funkce exsecans.
I exsecans je dnes spíše historickou matematickou funkcí. Výpočetní technika vytlačila potřebu této specifické funkce – opět ji lze snadno dopočítat:
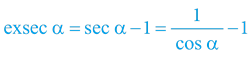
V dávných dobách však kalkulačky neexistovaly a tabulky trigonometrických funkcí pracovaly i s funkcí exsecans, která má přímou fyzikální interpretaci v kinematice i astronomii. Například spisy Galilea pracují s funkcí exsecans poměrně frekventovaně!
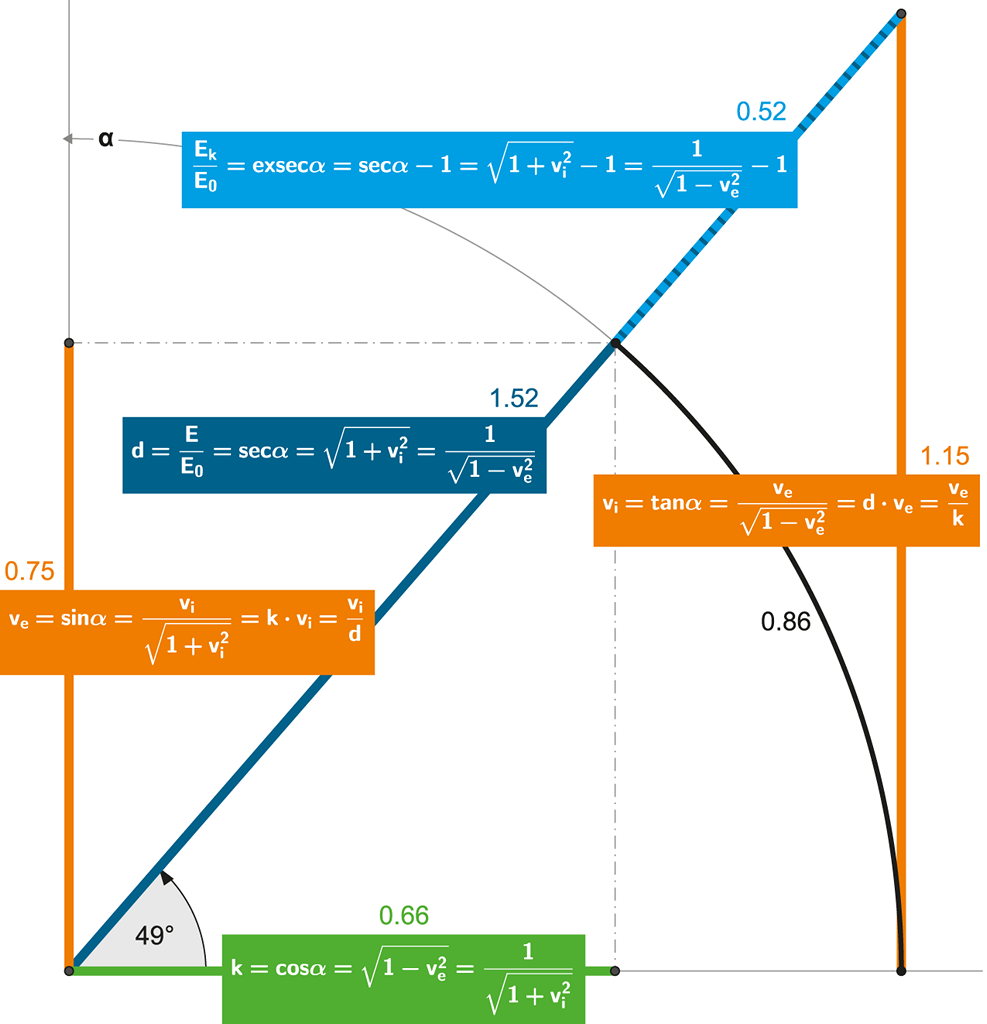
Obrázek 112:
Jednotková kružnice s vyjádřením všeho možného.
Z výšeuvedeného plynou i obecné vztahy pro celkovou a kinetickou energii:
3.4.6.1 CELKOVÁ ENERGIE
Dle jednotkové kružnice i výšeuvedeného:
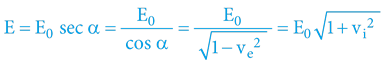
Pro staromilce:
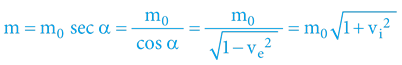
3.4.6.2 KINETICKÁ ENERGIE
Dle jednotkové kružnice i výšeuvedeného:
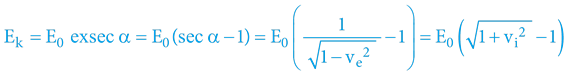
Pro staromilce:
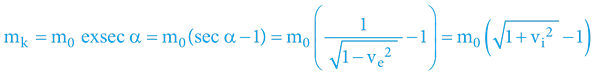
3.4.6.3 CELKOVÁ ENERGIE V ČASOPROSTOROVÉ KRUŽNICI
Výšeuvedené zobrazení časoprostorové kružnice zobrazuje pouze „poměrové“ vyjádření energetické bilance – délka úsečky v časoprostorové kružnici udává pouze poměr E/E0 či Ek/E0, respektive situaci tělesa o „jednotkové“ primární energii.
Nicméně – pomocí plochy obdélníků můžeme v jednotkové kružnici vizualizovat dokonce i energii těles o libovolné primární hmotnosti:
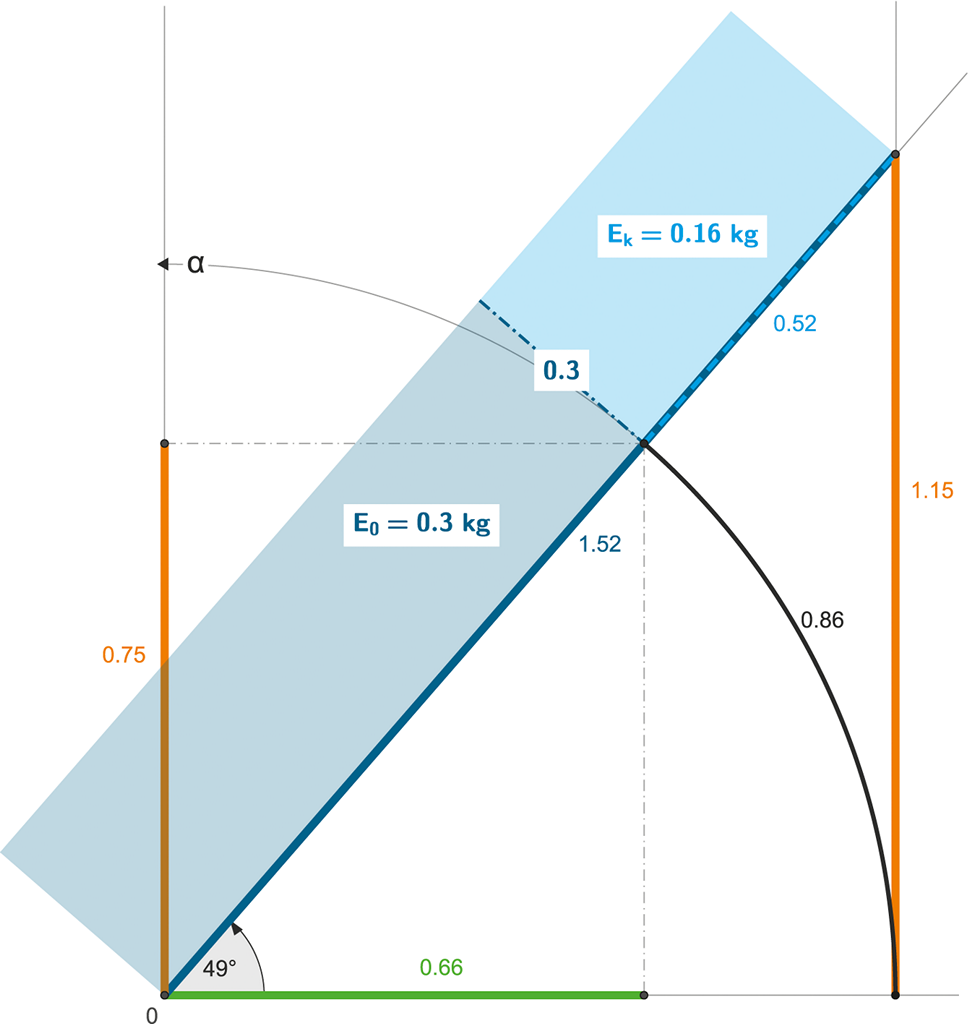
Obrázek 113:
Plocha obdélníků zobrazuje celkovou energii (0,46 kg) rozdělenou na kinetickou energii (0,16 kg) a primární energii objektu (0,3 kg).
3.4.6.4 PRIORITA TRIGONOMETRICKÝCH FUNKCÍ
V jednotkové kružnici můžeme přepočítávat hodnoty navzájem mezi sebou buď na základě Pythagorovy věty (vystačíme s mocninami a odmocninami), anebo na základě trigonometrických funkcí.
V rámci TČ upřednostňujeme trigonometrické funkce, mají totiž přímou geometrickou interpretaci v jednotkové kružnici, respektive v Euklidovském „kolmém“ prostoru – jsou tudíž „názornější“. Navíc – s pomocí trigonometrických funkcí vždy vede k cíli méně matematických operací!
Moderním počítačům či vaší kalkulačce je lhostejno, zda mají spočítat sinus či druhou odmocninu – obě úlohy vedou k „nekonečným“ aproximacím pomocí polynomických řad. Trigonometrické vyjádření je proto ve výsledku zpravidla výrazově kratší (méně matematických operací) a výpočetně srovnatelné s alternativním výrazem (mocniny a odmocniny).
Výšeuvedené nemění nic na skutečnosti, že i klasická podoba vztahů pro přepočet jednotlivývh veličin je velmi jednoduchá a „elegantní“ – například matematika pro přepočet rychlostí:
Chceme-li přepočítat rychlosti „nahoru“:
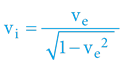
Chceme-li přepočítat rychlosti „dolů“:
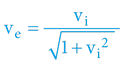
3.4.6.5 PODOBNOST S MATEMATIKOU TR
Pakliže bychom rychlost nevyjadřovali v bezrozměrných jednotkách (podílem v/c), spatřili bychom v některých výšeuvedených matematických vzorcích vtahy klasické relativistické fyziky:
V našem případě jsme však všechny vztahy odvodili pouze na základě matematiky pravoúhlého trojúhelníku 4D prostoru, potažmo trigonomaterických funkcí v jednotkové kružnici.
Opět platí, že získané matematické vztahy popisují jakékoliv dynamické jevy obecně, nikoliv pouze kinematiku vysokých rychlostí:
Například vzorec pro výpočet kinetické energie Ek = E0 excec α = m0 exsec α je obecnou variantou přibližného vztahu Ek = ½ mv2, který jsme se kdysi všichni učili v hodinách fyziky. V nízkých rychlostech (cca do α = 5°) je totiž exsecans úhlu přibližně roven hodnotě vypočtené dle vzorce ½ v2 (ať již použijeme vi, či ve; neb obě rychlosti jsou pro takto malý úhel de facto totožné).
Ve vyšších rychlostech však přestává přibližný vzorec ½ v2 „fungovat“ a je potřeba užít univerzálních vztahů jednotkové kružnice, respektive trigonometrie.

