3.4.8 CESTOVÁNÍ KE HVĚZDÁM
Astrofyzikové i obyčejní lidé si rádi kladou teoretickou otázku, jak daleko do vesmíru bude moci jednou lidstvo proniknout. I když je zřejmé, že technologický pokrok lidstva zatím neumožňuje odpovědět na tyto otázky reálným experimentem – teoreticky je úloha poměrně snadno řešitelná.
Typickým scénářem je rovnoměrně zrychlený pohyb s „rozumným“ zrychlením (nejlépe identickým zemskému gravitačnímu zrychlení).
Klíčem je opět korektní pochopení 4D prostoru – jako užitečná pomůcka znovu poslouží „jednotková“ kružnice:
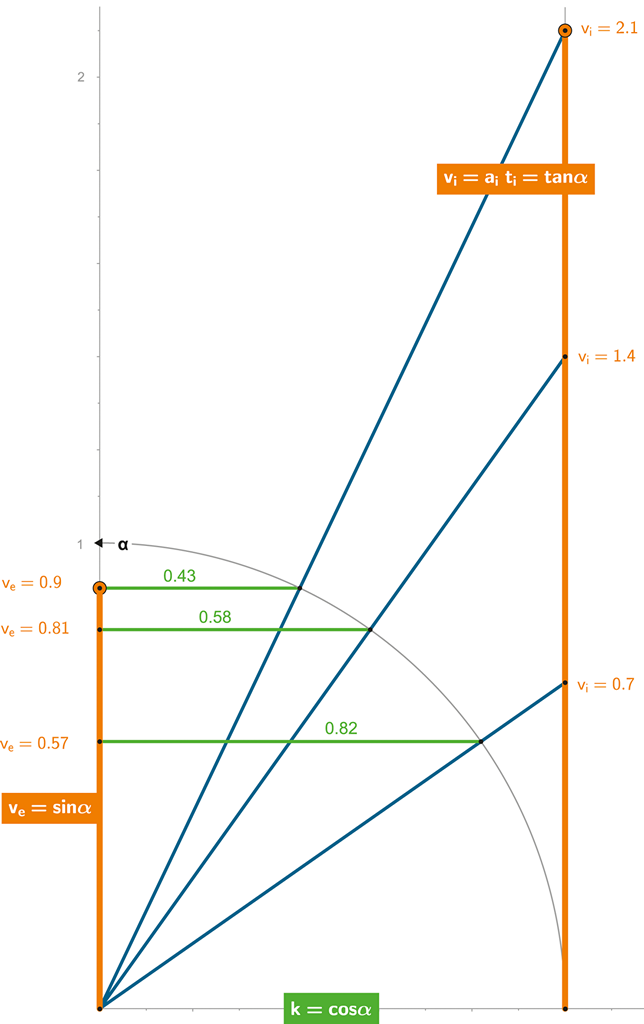
Obrázek 114 + ANIMACE:
Zatímco interní rychlost (tangenta) roste lineárně, externí rychlost (sinus) zpomaluje spolu s kontrakcí času (cosinus).
Výšeuvedený diagram znázorňuje, jaká bude matematika jednotkové kružnice při rovnoměrně zrychleném pohybu:
Pro interního astronauta vesmírné mise se nebude dít nic „nestandardního“ – jeho rychlost bude narůstat bez omezení – lineárně s časem:
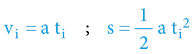
Pohledem do dalekohledu směrem k matičce Zemi (či měřicí aparaturou) však astronaut zaznamená, že čas na Zemi se zrychluje oproti jeho času (poměr určuje secans v diagramu).
Inverzní situaci zaznamenají pozorovatelé ze Země vůči astronautovi – z jejich perspektivy budou hodiny astronauta zpomalovat (poměr určuje cosinus v diagramu), a stejně úměrně bude zpomalovat i rychlost externě naměřená astronautovi, limitně se blížící ve = c = 1.
Zpočátku vesmírné mise (prostorový úhel max. 5 %) budou naměřené hodnoty (časů a rychlostí) obou stran téměř totožné, ale s rostoucí dobou letu (rostoucí rychlostí) bude z pohledu astronauta čas Země čím dál více zrychlovat; optikou Země bude naopak čas i rychlost astronauta zpomalovat – v souhrnu tak bude časová disproporce stále rychleji narůstat.
Takovýto fenomén již není možné smysluplně znázornit graficky, nicméně jej lze poměrně snadno spočítat – díky integrálnímu počtu:
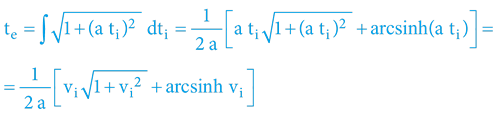
Jde o jeden z mála matematických vztahů v této knize, kde jsme na okamžik trochu překročili meze středoškolské matematiky, nicméně stále jde jen o integrování „Pythagorova trojúhelníku“ – žádná další „kouzla“.
Integrál v tomto scénáři totiž de facto pouze „sčítá“ sekanty úhlů, které jsou definovány lineární změnou tangenty. Milovníci trigonometrických funkcí totiž na jednotkové kružnici zřetelně vidí, že výšeuvedenou rovnici lze zapsat i v alternativní formě:
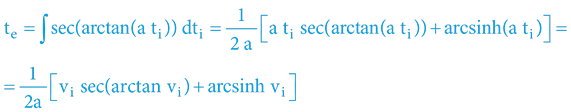
A uvědomíme-li si, co výšeuvedené matematické výrazy vyjadřují ve fyzikálním významu, lze rovnici dále vyjádřit třeba i takto:
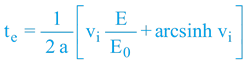
Přičemž:
vimaximální dosažená rychlost rovnoměrně zrychleného pohybu z pohledu interního účastníka vi = a ti
azrychlení
E/E0vyjadřuje nutný nárůst celkové energie (hmoty) kosmického modulu
arcsinhinverzní hyperbolická funkce
Hyperbolické funkce (viz arcsinh) jsou příbuznými trigonometrických funkcí – jde o analogii jednotkové hyperboly vůči jednotkové kružnici. V reálném světě mají hyperbolické funkce častou fyzikální interpretaci – viz například tvar prověšeného elektrického vedení mezi dvěma sloupy.
A jaké možnosti skýtá takováto matematika pro lidstvo?
Vzpomeňme na kapitolu Cestování ke hvězdám dle TR, kde jsme upozornili na přílišný „optimismus“ matematiky plynoucí z TR. Situaci jsme ilustrovali na idealizovaném „typickém“ scénáři vesmírných letů:
Astronauti poletí s konstantním zrychlením v hodnotě shodné s pozemským tíhovým zrychlením a = g = 9,81 m/s2. První polovinu letu budou astronauti zrychlovat, druhou brzdit – vždy se stejným zrychlením/zpomalením, které de facto vytvoří na palubě lodi konstantní pozemské podmínky pro organismus posádky.
Podle TR lze takovýmto scénářem za 19,8 palubního roku dosáhnout středu naší galaxie (vzdáleného cca 27 000 světelných let), zatímco na Zemi mezitím uplyne 27 002 roků! Ba co víc – za 45,2 palubního roku lze takovýmto scénářem doletět až k hranicím viditelného vesmíru (vzdálených cca 13 000 000 000 světelných let), zatímco na Zemi mezitím uplyne 13 000 000 002 roků!
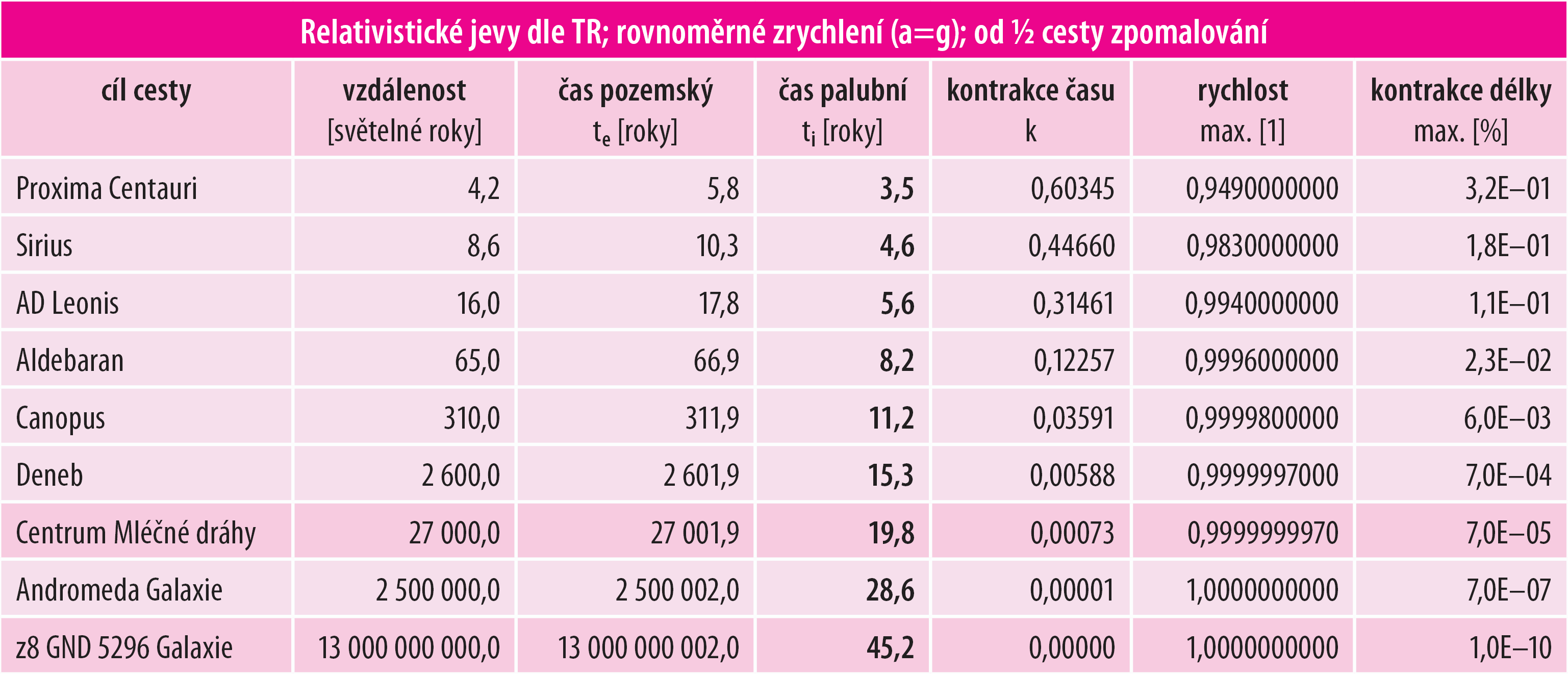
Tabulka 5: Scénář TR je „podezřele“ optimistický
Nabídne TČ a jednotková kružnice 4D prostoru také podobně fantaskní předpovědi? Stačí se zeptat výšeuvedené rovnice:
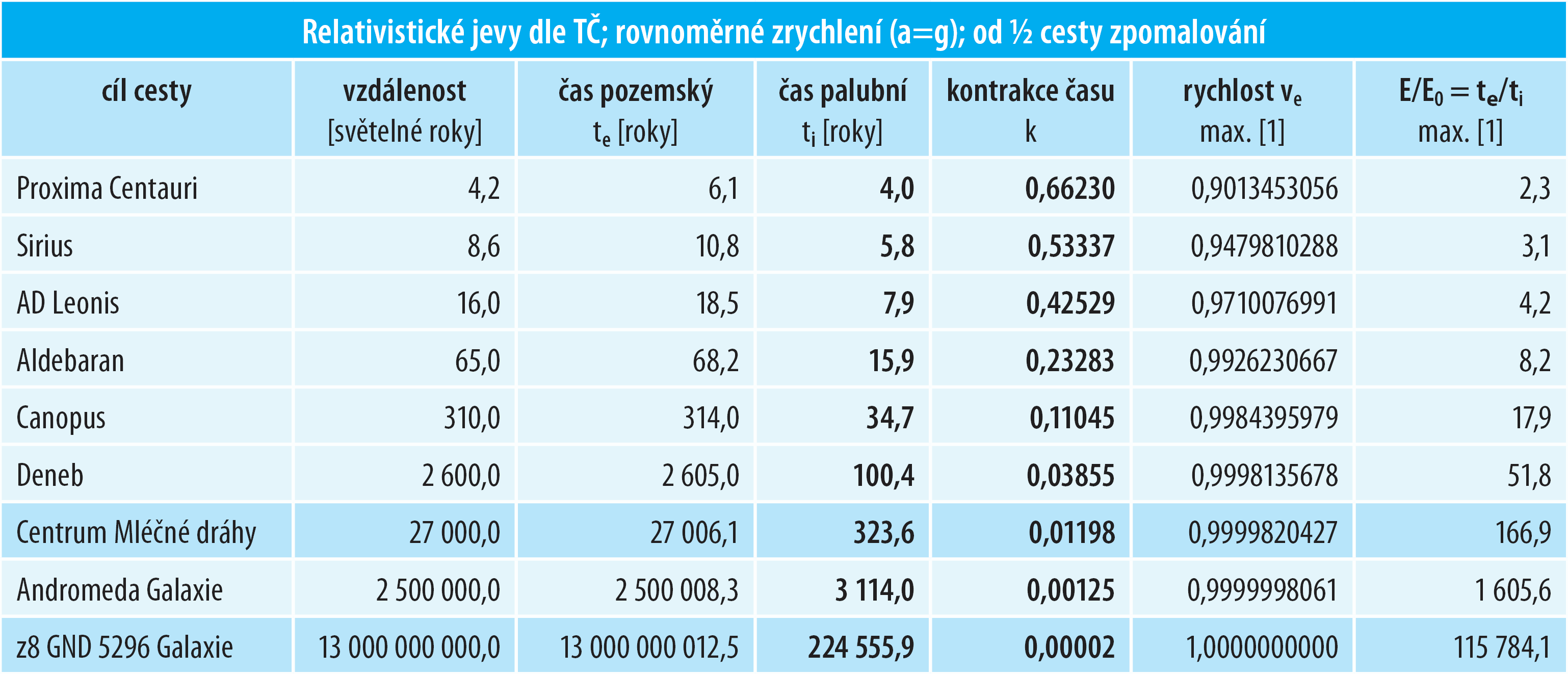
Tabulka 6: Teorie času je střízlivější …
Jak je vidno – TČ není zdaleka tak optimistická jako TR.
Čísla v obou teoriích přitom vznikla podobným způsobem – integrálním počtem (podle času), avšak rozhodující je korektní „uchopení“ 4D časoprostoru, abychom integrovali podle „správného“ času.
V dané souvislosti je tato kapitola i odpovědí na otázku, zda se TČ a TR opravdu nějak zásadně liší – zda nejsou obě teorie jen alternativním pohledem na stejnou fyzikální realitu.
Výšeuvedená čísla demonstrují, že na korektním uchopení matematiky časoprostoru opravdu záleží:
Lidstvo bude zcela jistě jednou plánovat svou misi ke středu naší galaxie a v takovém případě je nezbytné vědět, zda bude plánovaná doba letu 20 či 324 let! Chyba ve fyzikálním uvažování by totiž byla v podobném případě fatální. Matematika pravoúhlého trojúhelníku (jednotkové kružnice) nám sděluje, že za 20 let s „pozemským“ zrychlením/zpomalením do centra galaxie rozhodně nedoletíme!
TČ má však i jednu dobrou zprávu:
Energetická bilance takovéhoto scénáře je dle TČ příznivější. Poslední sloupec druhé tabulky (dle TČ) říká, jakým poměrem musí narůst celková energie posádkového modulu, aby taková loď vůbec měla dostatek „paliva“ pro svůj let do centra galaxie (neboť každý přírůstek rychlosti znamená přírůstek kinetické energie, respektive nárůst celkové energie, respektive hmotnosti).
Dle TČ musí narůst primární energie (hmotnost) kosmické lodi na 167násobek, což je sice obrovské číslo, nicméně TR uvádí pro stejný scénář více než 14tisíci-násobek!
V každém případě je zřejmé, že lidstvo bude moci uvažovat o podobných scénářích teprve tehdy, až se naučí využít energii hmoty se 100% účinností – „čistou“ bezodpadovou formou (třeba anihilací hmoty a antihmoty). I v takovém případě však bude muset vesmírná mise startovat se 167 kilogramy paliva na každý jediný kilogram posádkového modulu.
O všech těchto otázkách nyní můžeme pouze spekulovat a fantazírovat – technologicky je lidstvo v tomto ohledu stále ještě v kolébce. Zákon zachování energie (hmoty) však bude platit za všech okolností!

