3.5.10 RESUMÉ K ZÁKONU SYMETRICKÉHO POHYBU
ZSP:
Množina lokálně izolovaných hmotných objektů se vždy pohybuje symetricky vůči svému hmotnému středu ve 4D Euklidovském prostoru tak, že se poloha toho středu v prostoru zachovává.
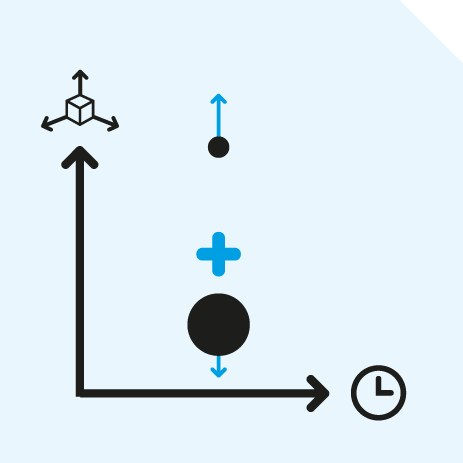
Abychom pochopili Zákon symetrického pohybu (ZSP), musíme jednou provždy zapomenout na zlozvyk mnoha generací fyziků, kteří formulovali pohybové zákony v jednotném čísle – což odporuje základnímu principu pohybu.
Pohyb se vždy týká více objektů! Rozpohybovat jeden jediný objekt, aniž by se pohybovalo něco jiného – je nemožným scénářem a nesmyslnou fyzikální představou. Aby se nějaká hmota mohla pohybovat jedním směrem – musí se jiná hmota pohybovat směrem opačným. Jinak to nejde!
Výšeuvedené občas ignoruje i vědecká obec:
Čas od času vznikne skvělé audiovizuální dílo ve snaze o popularizaci vědy a jedním z nejlepších počinů novodobé historie byla i série Kosmos – časoprostorová odysea (Cosmos: A Spacetime Odyssey) z roku 2014, z dílny 21st Century Fox a National Geographic Channel.
I v této sérii se však opakuje fyzikální lapsus mnoha podobných vzdělávacích pořadů, kdy hlavní průvodce (astrofyzik Neil deGrasse Tyson) křižuje vesmír se svou vesmírnou lodí bez toho, aby byl pohyb lodi „vyvážen“ opačným pohybem něčeho jiného (například proudem fotonů či plazmy).
Opomenutí tak významného fyzikálního principu je v podobných vzdělávacích dokumentech velmi „nešťastným“ svědectvím faktu, že symetrie pohybu (zachování hybnosti) často uniká i fyzikům samotným. Tvůrci seriálu Star Trek by z mechaniky dostali evidentně lepší známku!
Teprve ve chvíli, kdy budeme pohyb zkoumat komplexně – všimneme si veledůležitého místa v prostoru, které je hmotným středem (barycentrem) zkoumané skupiny objektů.
Hmotný střed je totiž oním „vysněným“ místem v prostoru, vůči němuž není pohyb sledovaných těles relativní, nýbrž je absolutní! Hmotný střed je onou absolutní polohou v prostoru, vůči níž se veškerý pohyb odehrává.
S mírnou nadsázkou je hmotný střed oním „pevným bodem“, s jehož pomocí chtěl Archimedes pohnout zeměkoulí.
Odhodí-li 100kilogramový kosmonaut v prázdném vesmíru 10kilogramový medicinbal – jeho tělo při takovém sportovním výkonu vydá něco málo kinetické energie, respektive nepatrný zlomek kilogramu, o který kosmonaut „zhubne“. Tato nepatrná energie (kg) se však neztratí, nýbrž se rozdělí ve formě kinetické energie mezi kosmonauta a medicinbal – oba se začnou pohybovat od společného barycentra, kosmonaut desetkrát menší rychlostí nežli medicinbal, přičemž souhrnný přírůstek kinetické energie (kg) za oba objekty bude přesně odpovídat hmotnosti, o kterou kosmonaut při svém výkonu zhubnul.
Původní místo v prostoru, z něhož pohyb započal (barycentrum), přitom zůstane zachováno (byť prázdné) a bude kroužit po orbitě Země stejně tak, jako před začátkem experimentu kroužila soustava kosmonaut + medicinbal.
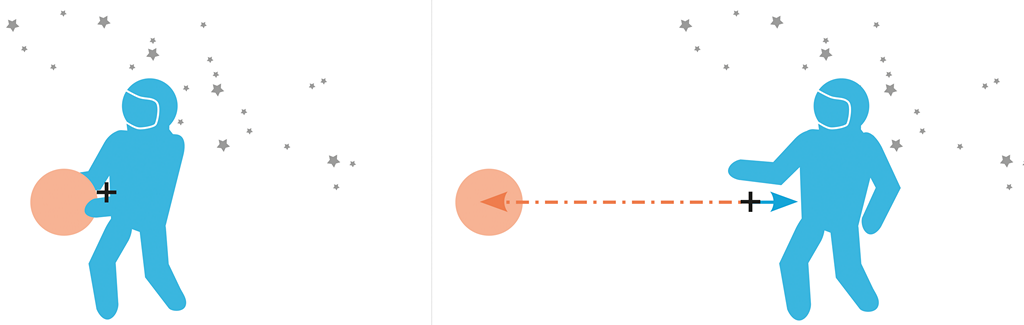
Obrázek 124:
Pohyb je vždy symetrický a barycentrum je vždy neměnné!
Na výšeuvedeném pohybu nebude nic „relativního“. Vůči společnému barycentru je možné vždy (před i po experimentu) objektivně určit, kdo se pohybuje více a kdo méně – komu stoupla energie (kg) více a komu méně – komu probíhá čas rychleji a komu pomaleji. Zcela exaktně je možné určit, kdo zaznamená vzájemnou dilataci času a kdo jeho kontrakci – byť v daném myšlenkovém případě půjde o de facto neměřitelné rozdíly.
Pakliže však na orbitě Země budeme experimentovat s většími energiemi – objekty se budou pohybovat významně rychleji a dilatace či kontrakce času se projeví zřetelným rozdílem naměřených rychlostí – v porovnání měření interních účastníků děje i externího pozorovatele (z pozice barycentra). Vzájemné rychlosti účastníků děje budou taktéž rozdílné a pro jejich určení je třeba použít matematiku „sčítání“ rychlostí – opět dle geometrie 4D časoprostoru.
Objekty se vzdalují přímočaře od společného hmotného středu:
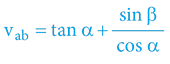
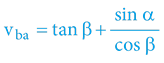
Objekty se pohybují kaskádovitě přímočaře:
vbc = tan γ = tan α + tan β
vcb = sin γ = sin (arctan (tan α + tan β))
Ať již se budou pohybového děje účastnit dva či tisíce objektů a vznikne tedy tisíce pohybových trajektorií – vždy se můžeme spolehnout na ZSP – hmotný střed zůstane vždy na svém původním místě v prostoru a vůči němu se vždy budou všechny objekty pohybovat takovým způsobem, aby soustava byla stále symetrická, respektive „těžiště“ zůstane vždy na stejném místě v prostoru a vždy vyvážené!

ZSP je univerzálním zákonem, který nám umožňuje řešit i složité soustavy mnoha těles. Faktická existence barycentra – jako zcela exaktního a neměnného místa v prostoru – činí Einsteinův „princip relativity“ nekorektním a naopak glorifikuje myšlenky Newtona, jehož 1. a 3. pohybový zákon jsou v synergickém spojení de facto identické se ZSP.
Odvozené zákony Newtonovy mechaniky – Zákon zachování hybnosti či Zákon zachování momentu hybnosti – jsou ve skutečnosti jedním z projevů ZSP. Jakmile použijeme Newtonovy pohybové zákony v kontextu 4D časoprostoru – výsledkem je ZSP a s jeho pomocí lze vyřešit jakékoliv pohyby – tedy i pohyby velkých rychlostí (velkých energií).
Pro „princip relativity“ žádný prostor nezbývá – pohyb vždy má, vždy měl a vždy bude mít objektivní charakter – ve vztahu k okolní hmotě (ke společnému barycentru), ve vztahu k časovým a rychlostním disproporcím, ve vztahu ke změně energie (hmotnosti).
Ať již budeme ze své pozemské laboratoře nazírat na pohyb rychlovlaku Maglev, GPS satelitu na orbitě Země anebo elektronu v LHC urychlovači – je zbytečné být na pochybách, kdo má v daném scénáři více pohybu:
Ve všech těchto situacích je totiž hmotným středem barycentrum „Zemské soustavy“, a právě toto místo v prostoru nám dává onen objektivní „pevný bod“ (v rámci lokálního uskupení objektů naší planety).
Externí optikou nehybného barycentra Země pak můžeme prohlásit:
• Nádraží (i laboratoře fyziků) na rovníku se vlivem rotace planety pohybují rychlostí 0,0000016 (465 m/s = 1674 km/h).
• Nádraží (i laboratoře fyziků) na 50° severní šířky se vlivem rotace planety pohybují rychlostí 0,0000010 (300 m/s = 1080 km/h).
• Nádraží (i laboratoře fyziků) na obou pólech planety se nepohybují vůbec!
• Vlak Maglev jedoucí po rovníku se pohybuje rychlostí buď 0,0000010 (297 m/s = 1069 km/h), anebo 0,0000021 (633 m/s = 2279 km/h), v závislosti na směru jízdy. Vůči nejbližšímu nádraží se však Maglev vždy pohybuje rychlostí 0,0000006 (168 m/s = 605 km/h).
• Vlak Maglev jedoucí po zemském pólu se pohybuje taktéž rychlostí 0,0000006 (168 m/s = 605 km/h).
• GPS satelity na orbitě Země se pohybují rychlostí 0,0000129 (3874 m/s = 13 946 km/h); vůči pozemním stanicím (jež jsou na povrchu planety, a nikoliv v jejím středu) však vždy o něco rychleji či pomaleji s ohledem na rotaci planety a orbitu satelitu (při takto nízkých rychlostech lze rychlosti obyčejně sčítat či odčítat).
• Elektron v urychlovači LHC se však pohybuje „závratnou“ rychlostí 0,999999991 (299 999 997 m/s), rotace Země je v tomto případě zanedbatelná.
Interní optikou pohybujících se objektů jsou naměřené rychlosti vždy větší, protože jejich čas plyne pomaleji (vůči středu planety):
• Lidé na rovníku mají kontrakci času 0,9999999999988, tedy prakticky neměřitelnou (řád 10‒12), a to nejen vůči středu zeměkoule, ale i vůči polárníkům!
• Cestující ve vlaku Maglev jedoucí po zemském pólu naměří vůči barycentru Země (anebo vůči lidem na nejbližším nádraží) kontrakci času 0,99999999999984, tedy opět prakticky neměřitelnou (řád 10‒13).
• GPS satelit naměří kontrakci času 0,99999999991662, tedy taktéž prakticky neměřitelnou (řád 10‒10), respektive měřitelnou pouze atomovými hodinami.
• Elektron v urychlovači LHC (7 TeV) má však kontrakci času 0,00013, čas tedy plyne elektronu 7454krát pomaleji a jeho „interní“ rychlost je 7454krát větší, tedy cca 2,2·1012 m/s !!!
V tomto ohledu vše „funguje“ spolehlivě a objektivně!
Zároveň je však nutné přiznat, že Zákon symetrického pohybu (ZSP) se hodí pro popis našeho světa jen omezeně – respektive, že tento zákon funguje v reálném světě pouze „teoreticky“ – pouze „přibližně“:
ZSP sice umí báječně popsat „vodorovný“ pohyb kulečníkových koulí, a dokonce zvládne detailně postihnout kinematiku stovek střepin granátu explodujícího někde v temném vesmíru, kam nesahá žádné gravitační pole …
Kde však na takovéto místo ve vesmíru narazíme?
Gravitace je totiž všudypřítomná!
V reálném světě bude tudíž trajektorie střepin granátu vždy nějak zakřivena a koule, která vypadne z kulečníkového stolu, rozhodně nebude pokračovat „v rovnoměrném přímočarém“ pohybu. Proč? Jaká skutečnost nám onen „dokonalý“ ZSP komplikuje?
Odpověď najdeme v další kapitole, která nás přinutí změnit náš dosavadní pohled na hmotu:
Mimo jiné se budeme muset rozloučit s představou vesmíru (našeho světa) v podobě ohraničených hmotných koulí – pohybujících se v „prázdnotě“ vesmírného vakua. Budeme se muset zamyslet nad otázkou: Co je to „hmotnost“ a kde se vlastně bere? … jež velmi úzce souvisí s jinou naléhavou otázkou: Jakým principem funguje „setrvačnost“ a kde se vlastně bere?
V reálném světě totiž objekty často mění svoji trajektorii i rychlost pohybu, aniž by na ně působila skutečná síla – bez jakýchkoliv setrvačných účinků – což je v rozporu s našimi běžnými zkušenostmi (zkuste například v autě popíjet kávu a zároveň prudce zatočit), respektive v rozporu s Newtonovými pohybovými zákony.
Při pohybu v „pustém“ vesmíru roste často reálným objektům rychlost, tedy energie (tedy i hmotnost), přičemž okolní prostředí (ve kterém se onen růst hmotnosti odehrává) se jeví „prázdné“ a bláhově jej nazýváme „vakuem“.
Je před námi veliký problém:
Zákon symetrického pohybu budeme muset přizpůsobit světu, v němž hraje hlavní roli GRAVITACE!

