JAK EINSTEIN ŠOKOVAL SVĚT
„Velkým cílem veškeré vědy je pokrýt co nejvyšší počet empirických poznatků logickým odvozováním z co nejmenšího počtu hypotéz či axiomů.“
Albert Einstein
Génius mladého Alberta Einsteina (1879‒1955) nespočíval v reálných fyzikálních experimentech.
Einstein prováděl své experimenty především ve své mysli – byl typickým představitelem teoretického fyzika, jehož způsob práce měl tolik společného s mnoha velikány historie jmenovanými v předešlých kapitolách.
Einstein vyšel ve své stěžejní teorii z myšlenek Galilea – konkrétně z principu relativity. Galileova primární úvaha směřovala k porovnání dvou pozorování – v podpalubí lodi stojící v přístavu a v lodi plující rovnoměrnou rychlostí. Galileo k tomu dodává:
„Pokud je pohyb lodi rovnoměrný, přímočarý, nepozorujete žádné změny na jevech a ani podle jednoho z nich nebudete moci soudit, zda se loď pohybuje, nebo stojí na místě. Pokud skočíte, doskočíte do stejné vzdálenosti na podlaze, jako kdyby byla loď v klidu, tj. neskočíte dále, pokud jste skočili proti směru pohybu lodi, i když se loď pohybuje velmi rychle; ačkoli dokud se vznášíte ve vzduchu, podlaha pod vámi utíká v opačném směru. Pokud hodíte něco svému příteli, nebudete muset házet větší silou, pokud on bude vpředu a vy vzadu, než v případě, že byste stáli obráceně. Kapky vody budou padat svisle dolů a ani jedna z nich nepadne více k zadní části lodi, ačkoli zatímco je kapka ve vzduchu, loď pluje dopředu…“
Princip relativity dle Galilea říká, že kinematické děje probíhají úplně stejně v nehybné soustavě i v soustavě pohybující se rovnoměrně přímočaře.
Výšeuvedené bývá interpretováno tak, že v podpalubí lodi (bez oken) nelze žádným experimentem určit, zda se loď pohybuje či nikoliv – pohyb je relativní.
Je lhostejno, zda budeme poznávat zákony fyziky a světa z pevniny či paluby lodi. Nemá smysl klást si otázku, zda je zkoumaný objekt v klidu, či pohybu – klid neexistuje – vždy je v pohybu vůči nějakému pozorovateli. Ostatně – celá naše planeta (fyzikální laboratoře, hvězdárny a observatoře) se pohybuje kolem Slunce a celá naše Sluneční soustava se pohybuje kolem centra naší galaxie (Mléčné dráhy).
Einstein již jako 16letý „provedl“ svůj veledůležitý myšlenkový experiment:
Kladl si otázku, co by se stalo, kdyby letěl zvyšující se rychlostí (hlavou kupředu) a držel před svým obličejem zrcadlo. Co by nastalo, kdyby dosáhl rychlosti světla?
V myšlenkách na svět s éterem (dle kterých se světlo pohybuje v éteru rychlostí 300 000 km/s) by fotony z Einsteinova obličeje nikdy nedostihly zrcadlo v jeho rukou, tím pádem by se neodrazily zpět k jeho očím – obraz v zrcadle by zmizel.
V takovém případě by však byl popřen Galileův princip relativity, neboť dle něj nelze žádným experimentem prokázat, zda se vědec pohybuje, či nikoliv.
Mladý Einstein si dlouho lámal hlavu, jak vyřešit tento myšlenkový rozpor, načež dospěl k závěru, že éter neexistuje. Došel tak (nezávisle) ke stejnému závěru, jaký naznačoval Michelsonův neúspěšný experiment se soustavou zrcadel.
Neexistuje-li éter a je-li pohyb relativní a je-li rychlost světla 300 000 km/s, a k tomu všemu musíme vysvětlit výsledky Michelsonových pokusů – jak to vše skloubit dohromady? Tyto otázky si kladl Albert Einstein několik příštích let a v roce 1905 svou odpověď našel – formuloval slavnou Speciální teorii relativity:
1.38.1 SPECIÁLNÍ TEORIE RELATIVITY (STR)
Teoretickým základem této slavné teorie jsou 2 Einsteinovy postuláty:
• Žádným pokusem nelze zjistit, zda se těleso pohybuje rovnoměrným přímočarým pohybem, nebo je v klidu. Jinými slovy: Ve všech rovnoměrně se pohybujících soustavách probíhají fyzikální děje stejně (platí pro ně stejné fyzikální zákony).
• Rychlost světla ve vakuu c = 300 000 km/s = 3·108 m/s je stejná pro všechny pozorovatele v rovnoměrně se pohybujících soustavách, a to ve všech směrech – nezávislá na rychlosti objektu vyzařujícího světlo. Jinými slovy: Pozorovaná rychlost světla je ve všech rovnoměrně se pohybujících soustavách vždy stejná.
První postulát není nic jiného nežli Galileův princip relativity. Teprve druhý postulát změnil zásadním způsobem pohled na svět:
1.38.1.1 SČÍTÁNÍ RYCHLOSTÍ
Do té doby, nežli myšlenky Alberta Einsteina přepsaly učebnice fyziky, platilo 0,5 + 0,5 = 1. Newtonův absolutní prostor a čas znamenal, že rychlost pohybu těles lze jednoduše sčítat i odčítat:
Lidstvo bude dozajista jednou schopno vytvořit vesmírnou loď (ať již s posádkou či pouhou umělou sondu), jež se vydá na dlouhou pouť vesmírem a bude schopna se od naší planety Země vzdalovat rychlostí 200 000 km/s. Teoreticky lze také uvažovat o tom, že takováto loď (A) bude mít i druhý pohonný stupeň (B) – a po dosažení cílové rychlosti se zapnou motory druhého stupně (B), které taktéž po čase dosáhnou cílové rychlosti 200 000 km/s vůči prvnímu stupni (A), z něhož byl druhý stupeň vypuštěn. Posádka (či přístroje) na palubě prvního stupně (A) naměří druhému stupni „rakety“ stejnou hodnotu 200 000 km/s, jakou pozemské řídicí centrum (C) naměří stupni prvnímu (A).
Podle standardního „logického myšlení“ (a Newtonových zákonů) by mělo řídicí středisko na Zemi naměřit druhému stupni rychlost dvojnásobnou, tedy 400 000 km/s.
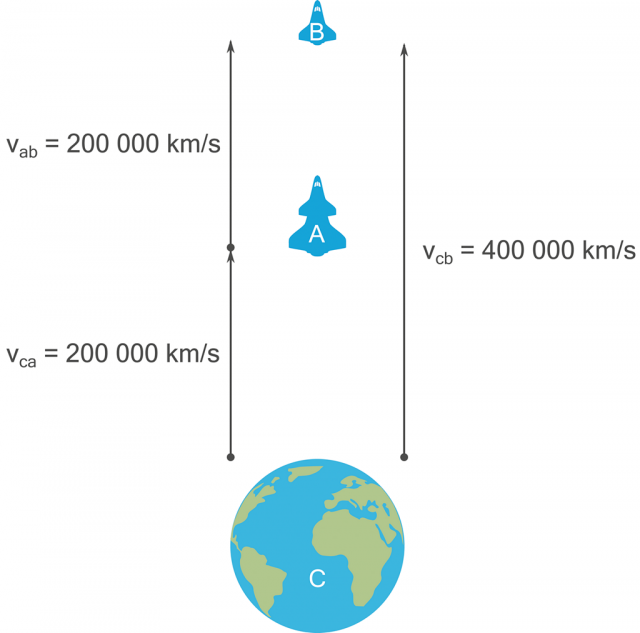
Obrázek 37:
Tradiční newtonovská (logická) představa „sčítání“ rychlostí.
Všichni známe takovéto logické skládání rychlostí z každodenního života – například po letišti se buď můžeme pohybovat pěšky rychlostí 4 km/h nebo můžeme stejnou rychlostí vejít na pás pohybující se rychlostí 5 km/h, čímž dosáhneme reálné rychlosti 9 km/h a zvýšíme tak svou šanci dojít včas na vzdálený odletový terminál.
Teorie relativity však obsahuje i druhý postulát, který sčítání rychlostí zásadním způsobem komplikuje. Říká, že ať již poletíme vstříc fotonům světla jakoukoliv rychlostí – vždy naměříme světlu stejnou rychlost (300 000 km/s)!
Například životodárné paprsky světla z našeho Slunce se k nám touto rychlostí šíří. A teď si představme, že úplně stejnou rychlost naměříme, ať již poletíme Slunci vstříc, či se od něj budeme vzdalovat!
Druhý postulát říká, že světlo se pohybuje „absolutní“ rychlostí a každý pozorovatel mu naměří vždy stejnou hodnotu, bez ohledu na relativní pohyb pozorovatele či relativní pohyb světelného zdroje, a že pohyby se vždy „sčítají“ tak, že výsledná rychlost se maximálně může limitně přiblížit rychlosti světla. Pro reálný hmotný objekt je samotná rychlost světla nedosažitelná – působení jakkoliv nezměrných sil či mnohonásobného sčítání pohybů nikdy neumožní dosáhnout plné rychlosti světla.
V důsledku 2. postulátu STR, pro náš výšeuvedený hypotetický příklad, tedy bude výsledná rychlost druhého stupně vesmírné lodi (B) vůči pozemskému řídicímu centru (C) nikoliv 400 000 km/s (1,33 c), ale 276 923 km/s (0,92 c)!
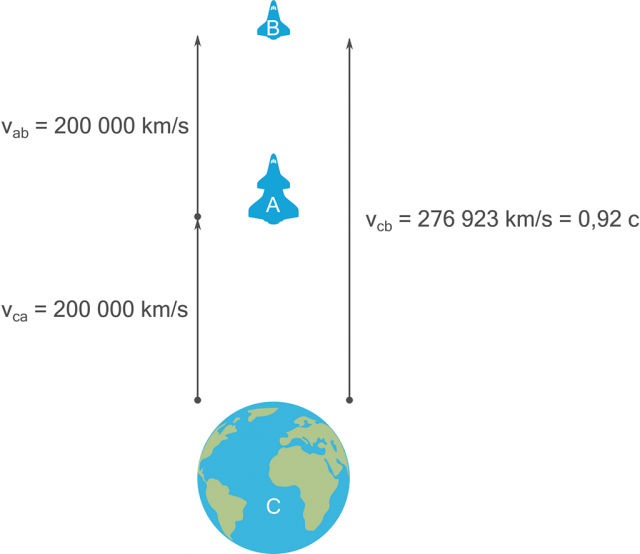
Obrázek 38:
Skládání rychlostí dle STR.
Rychlost světla je dle STR maximální možnou rychlostí, jakou se může ve vesmíru šířit hmota (tedy i informace). Světlo (elektromagnetické vlnění), respektive fotony – jejichž klidová hmotnost je nulová (fotony v klidovém stavu vůbec neexistují) – jako jediná forma hmoty se šíří onou hraniční maximální rychlostí. Větší rychlost než rychlost světla není dosažitelná! Všechny ostatní formy hmoty (neutrina, elementární částice, vesmírný prach, komety, planety, galaxie i uměle vytvořená kosmická plavidla jakéhokoliv druhu) se pohybují vždy pomaleji!
1.38.1.2 DILATACE ČASU
Einstein ze svých postulátů odvodil i další veledůležité konsekvence:
Dilatace času je zcela jistě nejvíce udivujícím fenoménem. Představa, že čas běží při vysokých rychlostech pohybu jiným tempem, je fascinující pro každého. O popularizaci (i určité znásilnění) tohoto fenoménu se postarali mnozí autoři vědecko-fantastických filmů a knih.
Způsobů, jak názorně objasnit dilataci času na základě Einsteinových postulátů, je mnoho, avšak nejrozšířenější se zdá být model s vlakem a „světelnými hodinami“.
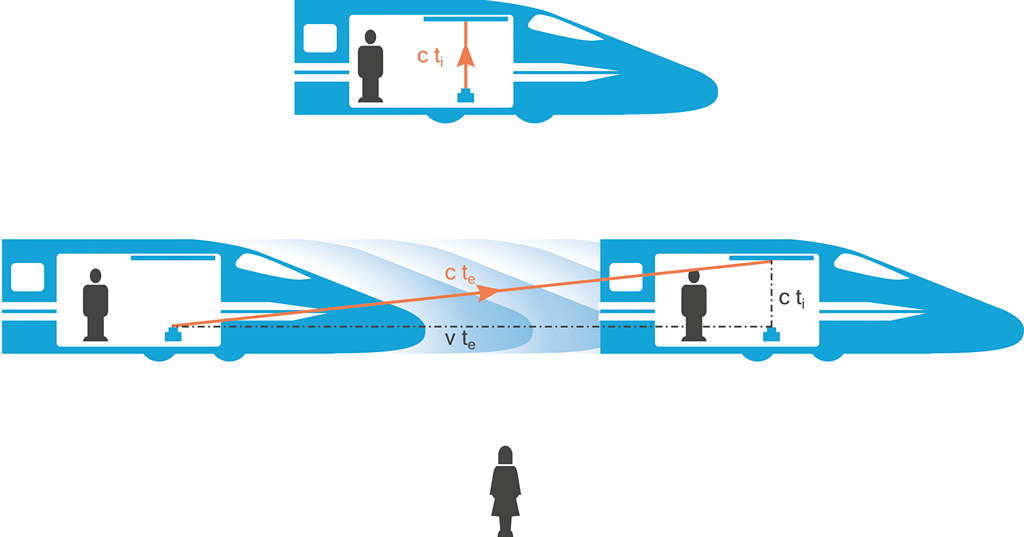
Obrázek 39:
Porovnání dráhy paprsku „světelných hodin“ z pohledu interního a externího pozorovatele.
Modelová situace dvou osob, z nichž interní účastník děje se nachází uvnitř pohybujícího se vlaku a externí pozorovatel sleduje celou situaci z nádražního nástupiště – vede v případě vlaku (s rychlostí pohybu srovnatelnou s rychlostí světla) k tomu, že externí pozorovatel bude pozorovat zřetelně větší dráhu paprsku světelných hodin nežli interní účastník uvnitř vagónu.
Z jednoduché matematiky trojúhelníku (Pythagorova věta) lze snadno určit vztah pro vzájemný poměr délek dráhy obou paprsků. Tento poměr bývá označován jako tzv. Lorentzův faktor:
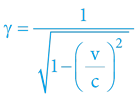
Z pohledu externího pozorovatele urazil paprsek světla evidentně delší dráhu, nežli by tvrdil interní účastník – dle výšeuvedeného vzorce.
A protože pro obě osoby platí základní vztah mezi dráhou, časem a rychlostí v = s/t (přičemž obě mají na paměti Einsteinův postulát o konstantní rychlosti světla) – delší dráhu (z pohledu externího pozorovatele) proto může světlo urazit jedině za delší čas! Externí pozorovatel (interního děje) proto pozoruje takový děj zpomaleně – a naměří na svých externích hodinkách pozorované události delší čas nežli interní účastník!
Z toho principu je tudíž odvozen termín dilatace času, ve smyslu prodloužení času.
Matematické vztahy pro přepočet časů jsou následující:
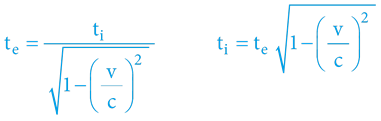
tečasový interval děje z pohledu externího pozorovatele
tičasový interval děje z pohledu interního účastníka
vrychlost pohybu objektu
crychlost světla
Časové trvání děje je optikou externího pozorovatele dilatováno (prodlouženo), respektive externí pozorovatel vnímá pozorované jevy tím více zpomalené (čas pohybujícího objektu zamrzá), čím více se rychlost pozorovaného objektu blíží rychlosti světla. Interní účastník pohybujícího se objektu tak stárne vůči externímu pozorovateli pomaleji a stejně zpomalené se jeví i hodiny umístěné v pohybujícím se objektu (a všechny fyzikální i biologické pochody).
Externí pozorovatel vnímá pohybující se objekt jako „zpomalený film“ – přičemž nejde o iluzi, ale o objektivní fyzikální realitu – zpomalení času a všech fyzikálních procesů pohybujícího se objektu potvrdí nejen „očitá“ svědectví externích pozorovatelů, ale zcela exaktně jej naměří i všechny externí měřicí přístroje a externí vědecké experimenty!
Příklad:
Vzdálenost ze Země na Měsíc je přibližně s = 3,8·108 m. Představme si kosmickou loď, jejíž motory dosáhnou 90% rychlosti světla, tedy její rychlost bude 2,7·108 m/s. Externí pozorovatel naměří, že takováto loď urazí vzdálenost ze Země na Měsíc za časový úsek te = 1,41 sekundy.
Kdyby externí pozorovatel během tohoto času pozoroval i hodiny na palubě lodi, viděl by (či zaznamenal svými externími měřicími přístroji), že interní čas na palubě lodi plyne zhruba poloviční rychlostí (44%) oproti jeho externímu času. Z pohledu interního účastníka by tak loď urazila vzdálenost ze Země na Měsíc za časový úsek ti = 0,62 sekundy.
1.38.1.3 KONTRAKCE DÉLEK
Dalším překvapivým (méně známým a méně populárním) důsledkem Teorie relativity je tzv. „kontrakce délek“. Logika je poměrně snadná – plyne z předchozích tvrzení:
V celém vesmíru pro kohokoliv platí obecný vztah, že rychlost = dráha / čas. Říkáme-li o světle, že se pohybuje rychlostí 3·108 m/s, pak tento údaj neznamená nic jiného, nežli že světlo urazí za časový interval jedné vteřiny dráhu 3·108 metrů. A dle STR musí toto platit pro kohokoliv!
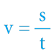
Princip dilatace času umenšuje „t“ ve výšeuvedeném vzorci. Má-li zůstat tato 3členná rovnice v platnosti, při změně jednoho člena musí být úměrně změněn i člen jiný.
Existuje-li dilatace času, pak je třeba buď připustit nadsvětelné rychlosti, nebo kontrakci délek. Nadsvětelnou rychlost TR nepřipouští, a proto je logickým důsledkem kontrakce délek:
Jestliže tvrdíme (při externím pozorování pohybujícího se objektu), že jeho běh času se nám jeví zpomalený (dilatovaný), musíme nutně akceptovat myšlenku, že prostorová vzdálenost ve směru pohybu (dráha pohybu) je pro interního účastníka ve stejném poměru zkrácena (kontrahována).
Pakliže bychom princip kontrakce délek nepřipustili, museli bychom takovému objektu přisoudit rychlost vyšší nežli rychlost světla – objekt by z pohledu interního účastníka urazil stejnou vzdálenost za kratší čas. Nadsvětelná rychlost však přímo odporuje základní filosofii TR:
V příkladu z minulé kapitoly jsme v závěru určili, že z pohledu interního účastníka – vzdálenost ze Země na Měsíc loď urazila za časový úsek ti = 0,62 sekundy. Bez úvah o kontrakci délek bychom v takovém případě nutně došli k závěru, že rychlost lodi z pohledu interního účastníka byla 6,1·108 m/s 3,8/0,62 = 6,1, tedy více než dvojnásobek rychlosti světla!
Princip kontrakce délek však situaci napravuje a stanoví, že z pohledu interního účastníka se vzdálenost ze Země na Měsíc zkrátí na 44 %, tedy na si = 1,7·108 metru. Výsledná rychlost pohybu je tak z pohledu obou osob (externího pozorovatele i interního účastníka) totožná v = si/ti = se/te = 2,7·108.
Interní účastník naměří oproti externímu pozorovateli kratší čas letu i kratší dráhu – obojí zkrácené ve stejném poměru. Oba pozorovatelé se tím pádem shodnou pouze na hodnotě rychlosti (jež je „podsvětelná“).
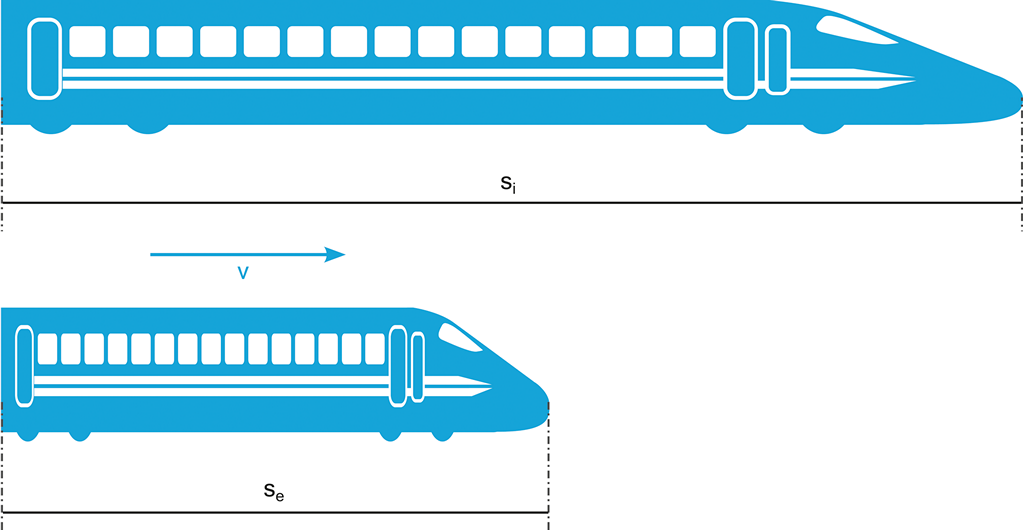
Obrázek 40:
Porovnání délek z pohledu interního a externího pozorovatele.
Délka (délka vzdáleností i délka předmětů) je tedy dle TR zkrácena stejným faktorem (Lorentzův faktor), jakým je dilatován čas:
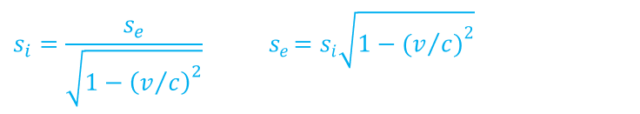
sedélka z pohledu externího pozorovatele
sidélka z pohledu interního účastníka
1.38.1.4 RELATIVITA SOUČASNOSTI
Pojem „současnost“ znamená shodnost časového okamžiku dvou či více událostí. Newton i spousta jeho předchůdců považovali čas a jeho chod za absolutní a nezávislý na ostatních jevech – proto i současnost byla absolutním pojmem.
STR však považuje současnost za relativní. Děje (prostorově od sebe vzdálené), které jeden pozorovatel označí za současné, označí jiný pozorovatel (pohybující se vůči prvnímu pozorovateli) za nesoučasné! Analogicky mohou být nesoučasné jevy pro jiného pozorovatele současné.
Důvodem je druhý Einsteinův postulát, respektive ona skutečnost, že světlo se šíří vůči komukoliv vždy konstantní a konečnou rychlostí.
1.38.1.5 RELATIVITA HMOTNOSTI
Einsteinova STR přináší i nový (relativistický) pohled na hmotnost – jako logický důsledek výchozích postulátů a předchozích závěrů:
Jestliže na základě dilatace času externí pozorovatel vnímá zpomalený čas pozorovaného jevu (všechny pozorované jevy trvají déle nežli z pohledu interního účastníka), má tento fakt přímý dopad na vnímání hmotnosti:
Einstein ve svých úvahách prováděl „myšlenkové experimenty“ ověřující Zákon zachování hybnosti (viz ZZ hybnosti) ve „vlaku“ pohybujícím se téměř světelnou rychlostí – například srážky dvou různě těžkých koulí – respektive úvahy o kulečníku ve vlaku.
Pro interního účastníka uvnitř vlaku bude Zákon zachování hybnosti fungovat „normálně“ – rychlost pohybu koulí bude inverzně úměrná jejich hmotnosti: p = m v
Externímu pozorovateli se však bude situace jevit opět nestandardně, a to v důsledku dilatace času, jež zpomaluje sledovaný pohyb – efekt „zpomaleného filmu“ snižuje hybnost pozorovaných předmětů.
Aby zůstal zachován Zákon zachování hybnosti, musí hmotnost růst s rychlostí stejnou měrou, jakou je zpomalován čas, a „kompenzovat“ tak zpomalování děje tím, že roste hmotnost – dle ZZ hybnosti:
Kopnou-li dva fotbalisté stejnou silou do dvou míčů a jeden z míčů se následně pohybuje pomaleji – vysvětlením může být jen jeho vyšší hmotnost!
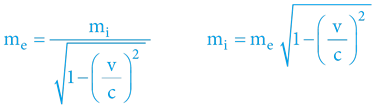
mehmotnost z pohledu externího pozorovatele
mihmotnost z pohledu interního účastníka
1.38.1.6 ÚMĚRNOST ENERGIE A HMOTNOSTI
Relativita hmotnosti – tedy skutečnost, že hmotnost roste s rostoucím pohybem – poměrně snadno vede i k nejslavnějšímu vzorci fyziky:
Obecně platí, že kinetická energie je integrálem rychlosti podle hybnosti. Hybnost přitom roste relativisticky dle Lorentzova faktoru (stejnou měrou jako hmotnost). Integrálním počtem lze relativně snadno odvodit onen veledůležitý vztah pro ekvivalenci hmoty a energie:
E = m c2
Díky této rovnici se svět zásadně změnil:
Skutečnost, že v kilogramu libovolné látky je vždy stejné množství energie (9·1016 Joulu), respektive 90 000 000 000 000 000 J (ať již jde o olovo či ptačí peří), je naprosto revoluční a nová! Věda, průmysl i armádní mašinérie staví na této rovnici své novodobé základy.
Ačkoliv je dnes odvození tohoto vztahu pro fyziky poměrně snadné, vztah E = m c2 nebyl přímou součástí Einsteinovy práce. Z historického hlediska je poměrně nesnadné určit, kdo je skutečným autorem obsahové a formální podoby této nejslavnější rovnice fyziky.
Při snaze o spravedlivost je potřeba vznik této rovnice datovat 1901‒1909 a její autorství přisoudit pánům: Walter Kaufmann, Albert Einstein, Max Planck.
1.38.2 JAK MINKOWSKI OBJEVIL ČASOPROSTOR
„Pohled na prostor a čas jako osamocené veličiny je napříště odsouzen ke zmizení do pouhé říše stínů.
Pouze určitým spojením obojího bude možné vysvětlit náš reálný svět.“
Hermann Minkowski
Hermann Minkowski (1864‒1909) se narodil v Litvě (tehdejší součást Polska) v rodině litevských židů. Studoval v Německu a jako profesor matematiky později učil na několika německých a švýcarských universitách. V Curychu byl mimo jiné i učitelem Alberta Einsteina.
V roce 1907 Minkowski rozvedl myšlenky Poincarého, který si uvědomil (1906), že principy STR lze názorně velmi dobře interpretovat ve čtyřrozměrné geometrii, kdy k běžnému Euklidovskému 3D světu přidáme imaginární čtvrtý časový rozměr.
Minkowski poprvé přišel s myšlenkou, že čtvrtý časový rozměr není pouhou pomocnou imaginární geometricko-matematickou konstrukcí, ale že svět (ve kterém žijeme) je skutečně čtyřrozměrný! Že čas a prostor nejsou dvě nesouvisející entity, ale že čas a prostor tvoří v našem reálném světě univerzální všeobjímající časoprostor, či chcete-li prostoročas!
Geniální Minkowski mohl dát vědě mnohem více, avšak ve věku pouhých 45 let zemřel na banální zánět slepého střeva. Jakou představu o světě nám Minkowski zanechal? Jakým způsobem jsou pojmy prostor a čas provázány? Jak si představit časoprostor?
Všichni jsme se ve škole naučili (a naše každodenní zkušenost to potvrzuje), že žijeme v 3dimenzionálním (3D) světě. Málokdo si však již vzpomene, že takovémuto vnímání světa říkáme Euklidovský prostor:
Náš 3D svět lze v takovémto pojetí vměstnat do prostoru, který je utvářen třemi kolmými rovinami, a stačí důkladně zakroutit hlavou, abychom si tyto 3 roviny (směry) uvědomili:
1. doleva – doprava (x)
2. nahoru – dolu (y)
3. dopředu – dozadu (z)
V hodinách matematiky a geometrie jsou pak tyto 3 roviny našeho světa nejčastěji reprezentovány 3D grafem s 3 osami (x, y, z).
Nížeuvedený obrázek schematicky demonstruje nejen náš 3D svět, ale i myšlenkový „vývoj“ od 1D světa k našemu 3D světu:
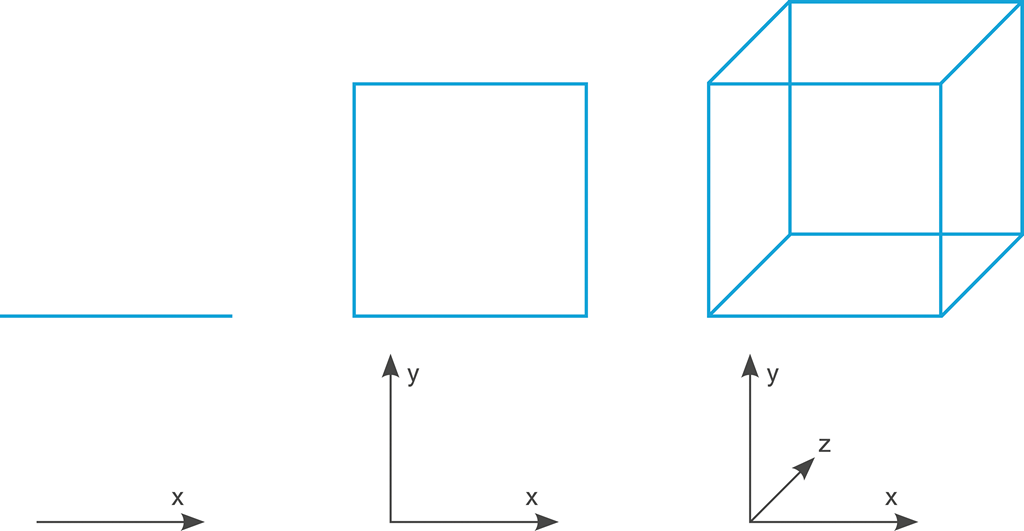
Obrázek 41:
Postupná „evoluce“ 1D prostoru ve 3D prostor.
Všimněme si jedné veledůležité vlastnosti:
Svět vyšší dimenze vzniká vždy tak, že přibude rovina (směr), která je kolmá na všechny původní roviny (směry)!
1.38.2.1 1D SVĚT
Svět 1D je tvořen pouhou přímkou:

Obrázek 42:
Úsečky jsou „bytosti“ v 1D světě tvořeném přímkou.
Potenciální 1rozměrné bytosti – úsečky – žijící v tomto světě znají jen jednu rovinu. Z našeho pohledu jsou „vězni“, kteří se mohou pohybovat jen vlevo či vpravo, avšak tyto úsečky si své vězení neuvědomují – ony nevidí jiné prostory a neumí si je ani představit. Pro ně je jejich svět stejně nekonečný jako ten náš – mohou nekonečně dlouho běžet kupředu (či dozadu) a nikdy nedojdou konce.
Tyto 1D bytosti mají na každém svém konci „laserové“ oko, které vidí jen a jen rovně před sebe – nevidí a nevnímá nic vlevo či vpravo, nahoře či dole.
Celý svůj život tyto úsečky spokojeně prožijí ve svém nekonečném světě a pomocí metru či pravítka umí tyto bytosti změřit vzdálenosti ve svém světě, a dokonce mohou i uspořádat Olympiádu a měřit, kdo z nich je nejrychlejší.
1.38.2.2 2D SVĚT
Svět 2D je tvořen plochou:
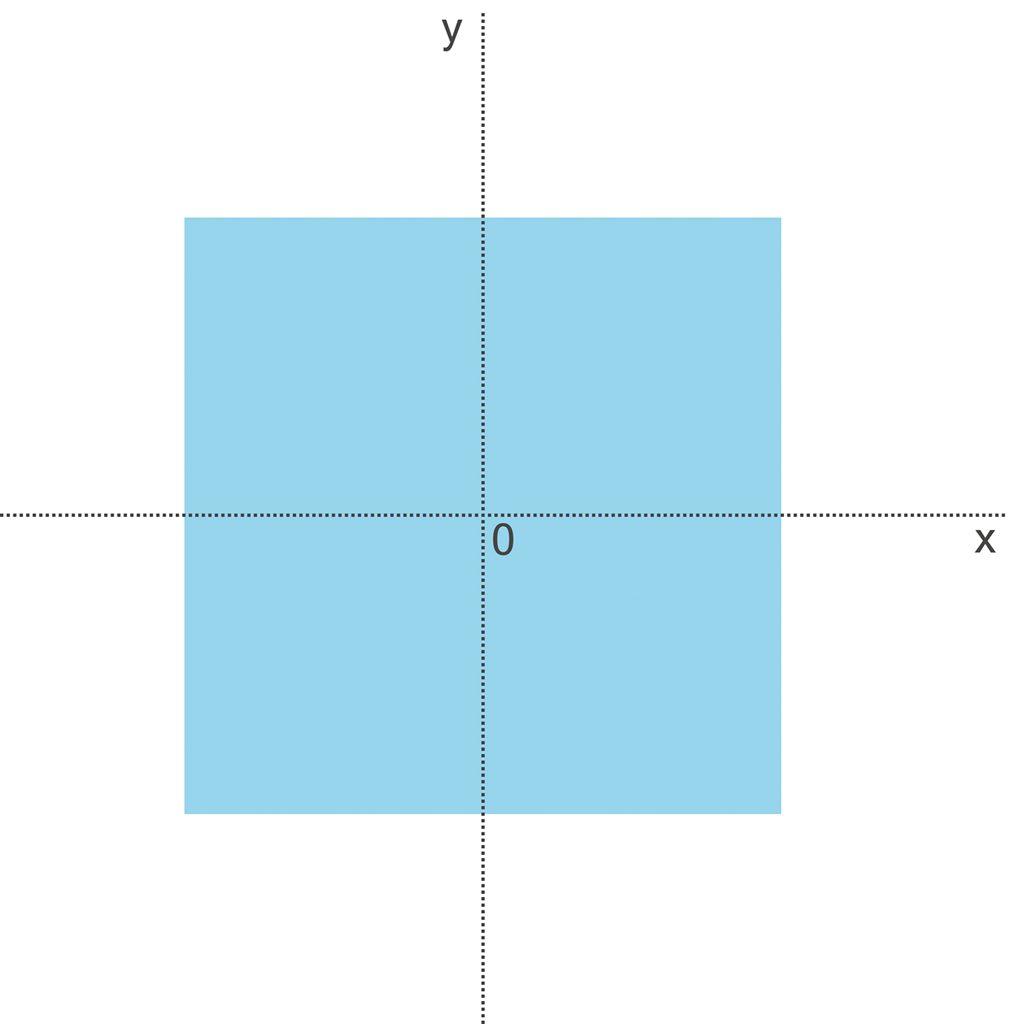
Obrázek 43:
Ploštice jsou „bytosti“ ve 2D světě tvořeném plochou.
Potenciální 2rozměrné bytosti – ploštice – žijící v tomto světě znají roviny dvě, a když pořádají závody v orientačním běhu, mohou běžet nejen vlevo či vpravo, ale i nahoru či dolu. Z našeho pohledu jsou i tyto bytosti „vězni“, avšak ani ploštice si své vězení neuvědomují – jejich „škvírovité“ oči nevidí náš třetí prostor a taktéž si jej neumí ani představit.
Celý svůj 2D život si ploštice spokojeně prožijí ve svém nekonečném světě a pomocí metru či pravítka umí taktéž tyto bytosti měřit vzdálenosti.
Ploštice jsou navíc velmi inteligentní a uvědomují si, že jejich 2D svět je tvořen dvěma (k sobě navzájem kolmými) rovinami. Znají proto 2D geometrii a znají i Pythagorovu větu:
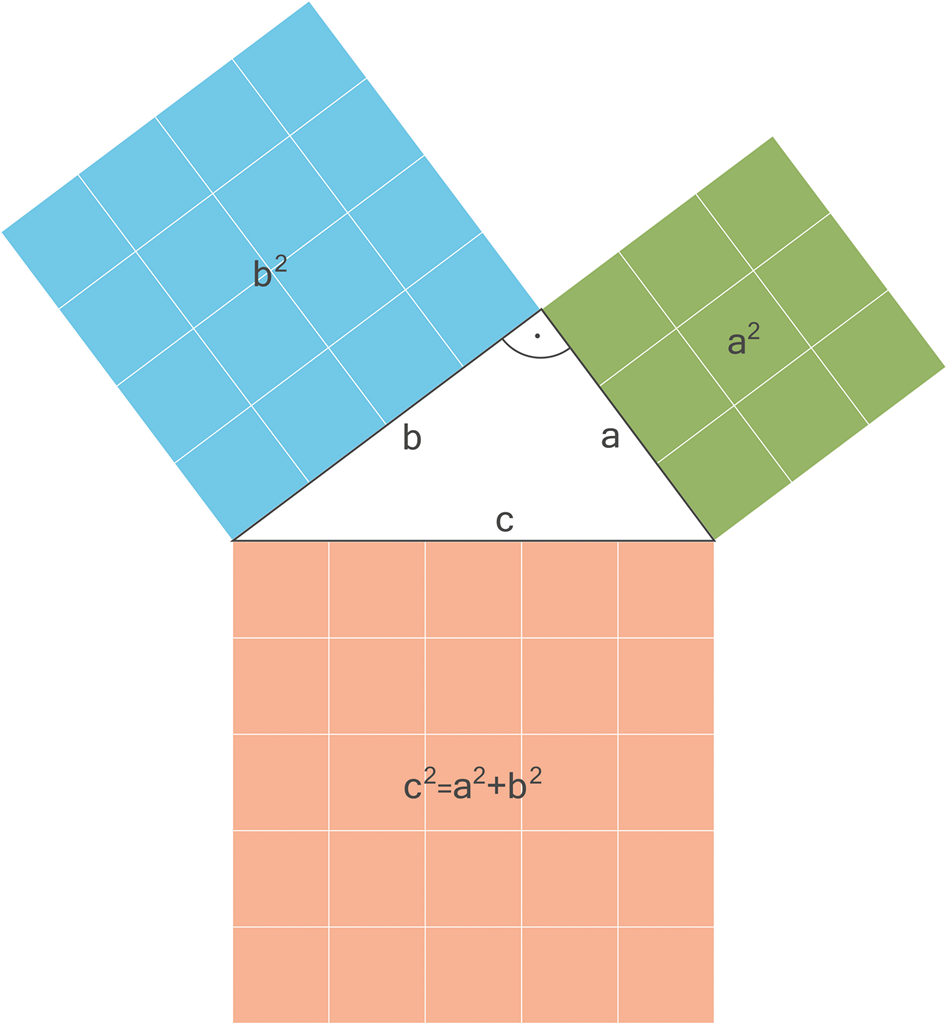
Obrázek 44:
Tuto matematiku známe všichni.

Ploštice umí nakreslit a spočítat všechny strany pravoúhlého trojúhelníka stejně tak, jako všichni absolventi našich základních škol. I ploštice ví, že půjde-li 8 metrů doleva a pak 7 metrů nahoru, celkově se ve svém světě vzdálí od původního místa na 10,6 metru:

1.38.2.3 3D SVĚT
3D svět je svět objemný:
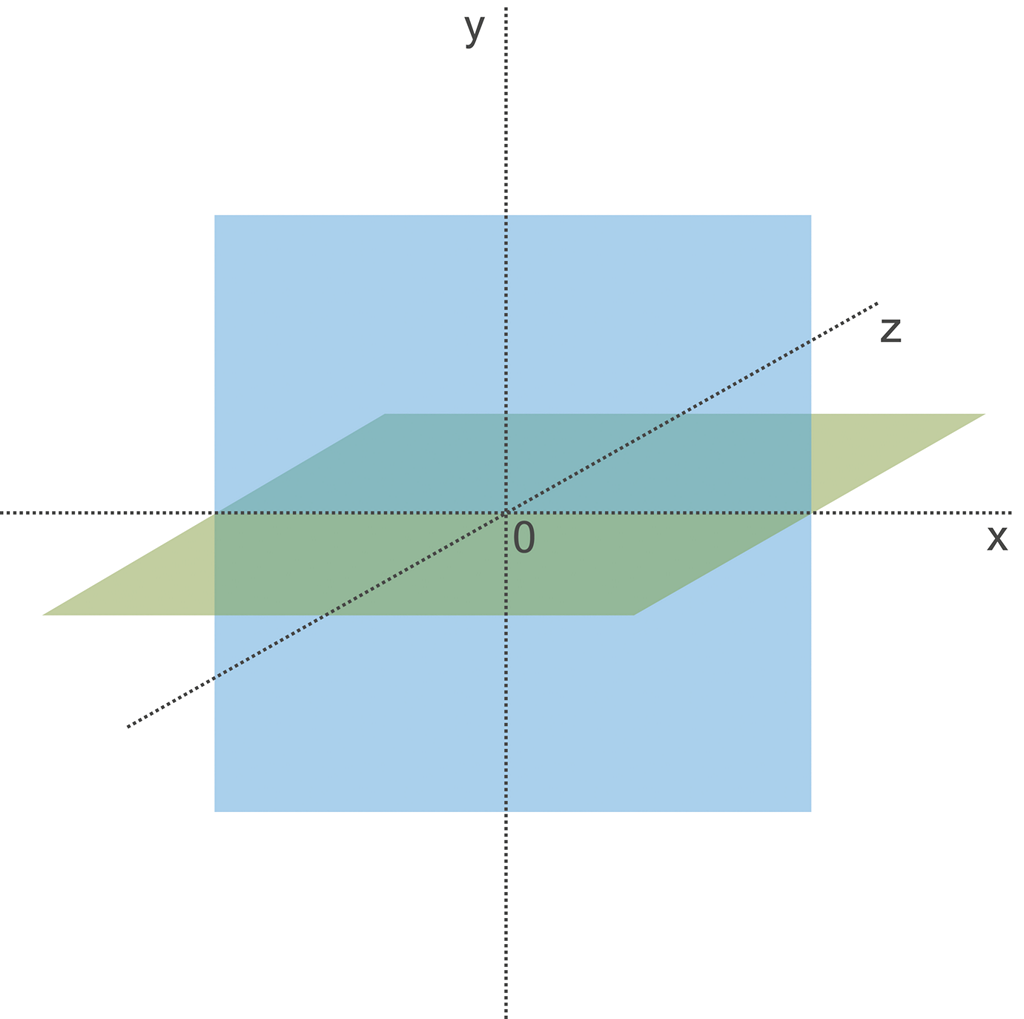
Obrázek 45:
Náš svět je tvořen 3D objemným prostorem.
Svět 3D – náš svět (jak je obecně vnímán) – je svět, v němž má vše svůj objem. Od plošného 2D světa se liší tím, že zde přibyla další rovina kolmá ke všem ostatním a tato rovina přidává hloubku původnímu 2D světu. Všechny bytosti v našem světě znají roviny tři, a když pořádají závody v orientačním běhu, mohou běžet nejen doleva či doprava a nahoru či dolu, ale i dopředu či dozadu.
Zůstává otázkou, zda si v analogii s předchozími jednoduššími světy budeme umět uvědomit, že i podstata našeho 3D světa „vězní“ naši představivost a znemožňuje nám pochopit, že dost možná existují i 4D světy i světy ještě početnějších rozměrů! Naše zrakové ústrojí vidí pouze 3D a stejně tak každodenní interakce s 3rozměrnými předměty nikterak nevytrénovala náš mozek, aby uměl vizualizovat svět 4D, natož světy ještě složitější.
Lidé 3D světa jsou taktéž velmi inteligentní a uvědomují si, že jejich 3D svět je tvořen třemi k sobě navzájem kolmými rovinami. Znají proto 3D geometrii a umí použít Pythagorovu větu i pro 3D aplikace:
I lidé umí nakreslit a spočítat všechny strany pravoúhlých trojúhelníků v prostoru. Člověk ví, že půjde-li 8 metrů doleva a pak 7 metrů nahoru, celkově se v plošné rovině vzdálí od původního místa na 10,6 metru (viz 2D svět).
Když pak člověk navíc popojde ještě 9 metrů dopředu, použije opět Pythagorovu větu a zjistí, že jeho finální vzdálenost v prostoru od původního místa je 13,9 metru:

1.38.2.4 ZOBECNĚNÍ MINKOWSKÉHO
Jak to vše souvisí s Minkowskim? A s Teorií relativity??
Minkowski a jeho následovníci (v tomto okamžiku možná i mnoho pozorných čtenářů) si uvědomili, že bez ohledu na omezenou představivost lidského mozku a navzdory skutečnosti, že 4D svět nelze v 3D světě přímo vizualizovat do podoby nějakého názorného obrázku či grafu – lze jej snadno spočítat!
Ať již žijete v 1D, 2D či 3D světě – vždy pro vás platí následující tvrzení:
• Možná jsem součástí nějaké vyšší dimenze.
• Neumím si ji sice představit, ale umím ji spočítat.
• V mojí interakci s vyšší dimenzí vždy platí Pythagorova věta (respektive matematika jednotkové kružnice a v ní vepsaného pravoúhlého trojúhelníku).
• Ať již se ve svém prostoru volně pohybuji jakýmkoliv směrem, rovina vyšší dimenze je vždy kolmá na směr mého pohybu.
Svět vyšší dimenze si nelze v nižší dimenzi přímo vizualizovat (představit)!
V našem světě lze proto obrázky (či nákresy) 4D světa ztvárnit vždy pouze omezeně tak, že při vizualizaci nahradíme jednu reálnou osu našeho světa osou imaginárního čtvrtého rozměru. Přestože jsou takovéto vizualizace přínosné pro pochopení matematicko-geometrických poměrů, jsou často pro náš mozek matoucí a je třeba si vždy uvědomovat omezenost takovýchto vizualizací.
1.38.2.5 4D SVĚT DLE MINKOWSKÉHO
Minkowski nebyl prvním, kdo myšlenkově experimentoval s představou času jako čtvrté dimenze. Byl však prvním, kdo tuto „fantaskní“ představu povýšil na realitu – na tvrzení, že fakticky žijeme ve čtyřrozměrném světě – nežijeme pouze ve 3D prostoru, ale žijeme ve 4D časoprostoru!
V době před Minkowskim pohlíželi fyzici na mechaniku všech dějů jako na 3D „představení v divadle“:
Bod a jeho pohyb v prostoru byl definován maximálně třemi délkovými souřadnicemi. Čas byl považován za jakýsi zvláštní fyzikální „parametr“ – za všudypřítomné (blíže nedefinované) fluidum, které je univerzální pro všechna místa ve vesmíru, všude je přítomen „zároveň“ a vždy „tiká“ stejným tempem.
Nepočítáme-li řecké filosofy, nikdo se před Minkowskim neobtěžoval zamyslet se nad otázkou: Co je to vlastně čas?
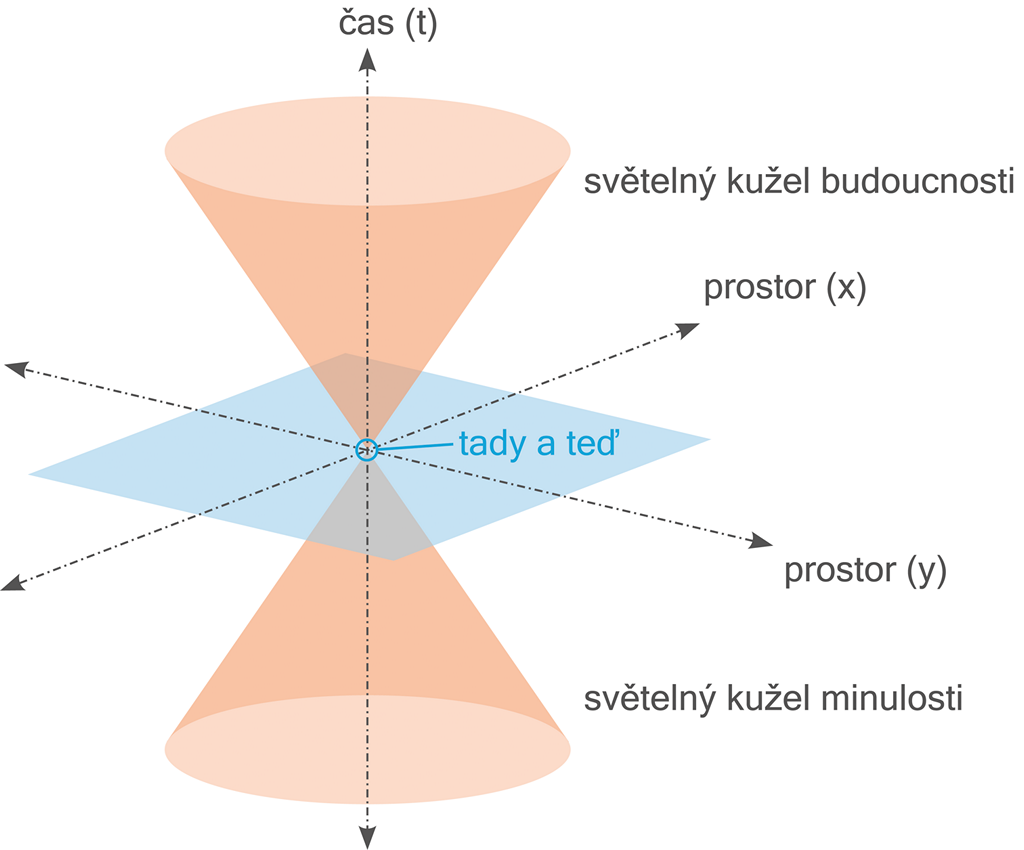
Obrázek 46:
Současné „standardní“ ztvárnění Minkowského 4D časoprostoru není příliš názorné.
Výše je zobrazena jedna z nejčastějších grafických interpretací Minkowského 4D časoprostoru. Znovu je v tomto ohledu třeba zdůraznit, že pokusy vizualizovat 4D svět na 2D papíře jsou málokdy skutečně názorné a myšlenkově uchopitelné! Často takové ilustrace přinesou více otázek nežli odpovědí – což platí i pro výšeuvedené zobrazení.
V dalších kapitolách se pokusíme přinést názornější vizualizaci 4D světa.
1.38.3 OBECNÁ TEORIE RELATIVITY (OTR)
„Je otázka, co je pro vědce významnější, zda znalost faktů či fantazie.“
Albert Einstein
Není bohužel možné detailně popsat OTR bez složité matematiky. Jde o „komplikovanou“ teorii (uceleně prezentovanou v roce 1916). Sám Einstein během svého života vtipkoval na téma, že on je jediným smrtelníkem, který správně chápe OTR.
Principy OTR však nikterak složité nejsou:
Primární myšlenkou, na které Einstein rozvinul svou OTR, bylo: „Když bude někdo padat volným pádem, nebude pociťovat svou vlastní váhu.“
Einstein byl touto myšlenkou šokován v okamžiku, kdy si ji uvědomil. Celá OTR je de facto pouze snahou o vysvětlení oné myšlenky – jež je na první pohled docela triviální, avšak ve skutečnosti v sobě skrývá veliký rozpor vůči Newtonovské fyzice.
Obecnou teorií relativity usiloval Einstein o nalezení „vnitřní krásy“ – ve snaze rozšířit působnost Speciální TR (vztahující se pouze na pohybové děje rovnoměrného pohybu) na všechny ostatní pohybové děje ve vesmíru – tedy i ty nerovnoměrné – probíhající se zrychlením/zpomalením či za působení sil.
A protože nejuniverzálnější silou vesmíru je síla gravitační, Einstein touto teorií primárně formuloval svůj názor na podstatu gravitace. OTR je především teorií gravitace a takto také bývá titulována.
Einstein při svých úvahách hledal odpověď na obecně známý a přitom důležitý jev – zjevné analogie mezi setrvačnou a gravitační hmotností těles (tento fenomén znal již Newton). V dennodenním životě se totiž setkáváme se dvěma projevy hmotností těles:
1.38.3.1 SETRVAČNÁ HMOTNOST
Setrvačná hmotnost – tuto hmotnost pocítíme, pokusíme-li se roztlačit (či naopak zastavit) pohybující se předmět:
Představme si nehybnou hladinu rybníka a na něm u mola volně splývající dvě plavidla – laminátový kajak a obrovitý parník. U kajaku nebude nikterak „těžké“ posunout jej silou paže vodorovně po hladině o jeden metr, kdežto u plně naloženého parníku lidská síla selže. Proč?
Na vině je samozřejmě rozdílná hmotnost obou plavidel, respektive Newtonův Zákon setrvačnosti.
1.38.3.2 GRAVITAČNÍ HMOTNOST
Gravitační hmotnost – tuto hmotnost pocítíme, pokusíme-li se jakýkoliv předmět zdvihnout do výšky. Zemská gravitace totiž všechny předměty přitahuje do středu Země. V analogii s oběma plavidly je opět zřejmé, že bude o hodně snazší vyzdvihnout z vody do výšky na úroveň mola laminátový kajak nežli plně naložený parník. Proč?
Opět je na vině rozdílná hmotnost, respektive Newtonův Zákon síly, respektive Newtonův Gravitační zákon.
1.38.3.3 ANALOGIE SETRVAČNÉ A GRAVITAČNÍ HMOTNOSTI
Že jsou si oba typy (projevy) hmotnosti v mnoha ohledech velmi podobné – věděli samozřejmě již všichni význační předchůdci Einsteina, včetně Newtona. Celá kinematika pohybu nebeských těles vychází de facto z poznatku, že setrvačná hmotnost = gravitační hmotnost.
Satelity na oběžné dráze kolem Země jsou vhodným příkladem:
Gravitační síla působí na satelit silou směřující do středu Země, a kdyby nebylo jiné síly – každý satelit by se brzy roztříštil o zemský povrch. Je tu však odstředivá síla kruhového pohybu satelitu, což není nic jiného nežli projev Zákona setrvačnosti – kdyby nebylo jiné síly, satelit by po přímce (tečně) opustil dráhu kružnice a vzdaloval by se do prostoru.
Setrvačná (odstředivá) síla satelitu je velikostně zcela stejná jako gravitační síla Země na satelit působící – obě síly jsou však opačného směru, a proto se vzájemně vyruší – satelit se ani nezřítí na povrch Země, ani neodletí do prostoru – pokračuje v rovnoměrném pohybu po kruhové dráze.
Na zcela stejném principu obíhá odnepaměti Měsíc kolem Země, Země (s Měsícem) kolem Slunce a Slunce (s celou naší Sluneční soustavou) kolem středu naší galaxie (Mléčná dráha).
Právě proto, že setrvačné a gravitační hmotnosti jsou totožné – proto celý vesmír funguje tak, jak má!
Kosmonauti na orbitální dráze se mohou spolehnout, že dostředivá gravitace i odstředivá setrvačnost se navzájem vyruší, ať již jde o jakkoliv hmotný předmět. Na oběžné dráze se proto ve stavu beztíže ocitne nejen mnohatunový obytný modul, ale spolu s ním i celá posádka, veškeré předměty na lodi i každá kapka vody. To vše proto, že gravitační a setrvačná hmotnost jsou analogické a velikostně totožné. Nezáleží na hmotnosti předmětu!
Jiným projevem tohoto fenoménu je fakt, že necháme-li v jeden okamžik padat z výšky libovolné předměty (holubí pírko, vejce, meloun, kovadlinu, padák či rogalo) a zanedbáme-li odpor vzduchu (necháme je padat ve vakuovém válci nebo na povrchu Měsíce), dopadnou všechny na zem současně!
Jak to vše souvisí s Einsteinem a OTR? Výšeuvedené přeci věděli již Einsteinovi předchůdci. Vše důkladně objasňují již Newtonovy pohybové zákony a jeho zákony o působení sil.
Einstein však našel „rozpor“ v klasických Newtonových zákonech a na základě tohoto rozporu zcela nově odůvodnil souvislost setrvačné a gravitační hmotnosti:
1.38.3.4 O GRAVITACI – EINSTEIN VERSUS NEWTON
Albert Einstein byl prvním, kdo zaznamenal zásadní rozpor v Newtonově teorii – rozpor gravitačního a pohybového zákona:
Podle 1. Newtonova zákona je nerovnoměrný pohyb (těleso mění směr pohybu, zrychluje či kombinace obojího) důsledkem působení síly!
Není-li přítomna vnější síla – musí se těleso pohybovat rovnoměrným přímočarým pohybem (nebo být v klidu). Je-li přítomna síla – těleso mění svou rychlost či směr pohybu – pohyb již není rovnoměrný či přímočarý. Zákon platí i inverzně – změna rychlosti či trajektorie vždy znamená přítomnost vnější síly.
Newtonovy zákony pociťujeme všichni v běžném životě:
Síla motoru automobilu způsobuje zrychlování, bez motoru jede auto po rovině konstantní rychlostí (zpomaluje pouze v důsledku odporu vzduchu a mechanických odporů). Síla motoru způsobuje akceleraci, síla brzd zpomalování – v obou případech nás setrvačné síly buď tlačí do sedačky, nebo do bezpečnostních pásů. Analogicky nás (i celý automobil) setrvačné síly v zatáčkách tlačí do stran, dělají nám nepořádek v kufru a rozlévají kávu.
Měří-li fyzik trajektorii automobilu na závodní dráze v čase, dokáže na základě Newtonových zákonů spočítat naprosto přesně síly působící na řidiče (i úhel naklonění hladiny kávy, kdyby byly závodní vozy vybaveny držákem nápojů), a to vše v každém místě tratě. V tomto ohledu fungují Newtonovy zákony spolehlivě – ať již jde o automobil, vlak, zaoceánský parník či bicykl – tam, kde je zrychlení, jsou i síly.
Výšeuvedené však platí pouze v případě, že závodní dráha je rovinná (nejsou stoupání, ani klesání)!
Einstein byl prvním, kdo si uvědomil, že při volném pádu Newtonovy zákony neplatí tak jednoznačně, jak jsou formulovány:
Postavíme-li na rovnou letištní plochu sportovní automobil, jehož motor udělí konstantní zrychlení a = 10 m/s2, pak zde Newtonovy zákony platí spolehlivě a hravě spočteme, že po 5 sekundách jízdy automobil urazí vzdálenost 125 metrů s = ½ a t2 a jeho finální rychlost bude 50 m/s, respektive 180 km/h v = a t, přičemž jezdce o hmotnosti 100 kg bude po celou dobu jízdy tlačit do sedačky síla 1000 N F = m a.
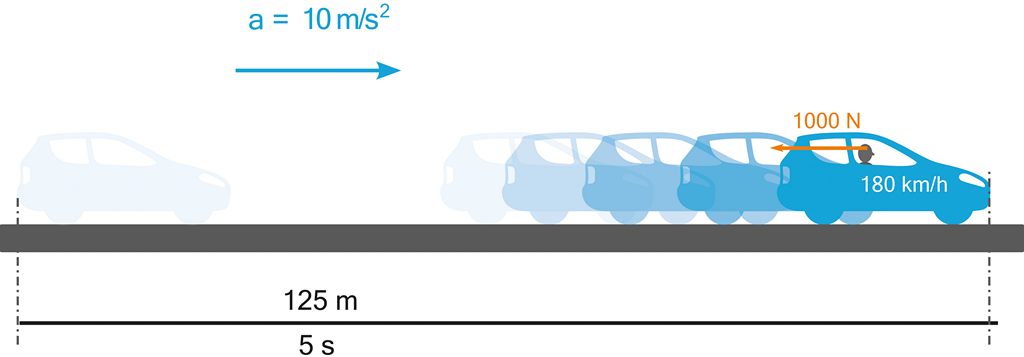
Obrázek 47:
Z nuly na 180 km/h za 5 sekund = velké zrychlení a velké přetížení!
Připevníme-li však stejný automobil na vrchol jeřábu ve výši 125 metrů nad zemí a necháme jej volně padat k zemi – analogie bude pouze zdánlivá a pouze z pohledu vnějšího pozorovatele:
Gravitační tíhové zrychlení Země je taktéž 10 m/s2, tudíž vnější pozorovatel naměří naprosto stejné parametry pohybu (zanedbáme-li odpor vzduchu nebo proběhne-li celý experiment uvnitř vakuového válce). Automobil se bude opět pohybovat rovnoměrně zrychleným pohybem, opět urazí dráhu 125 metrů za 5 sekund a opět bude mít na konci této dráhy finální rychlost 180 km/h (těsně před tím, nežli se roztříští o zem).
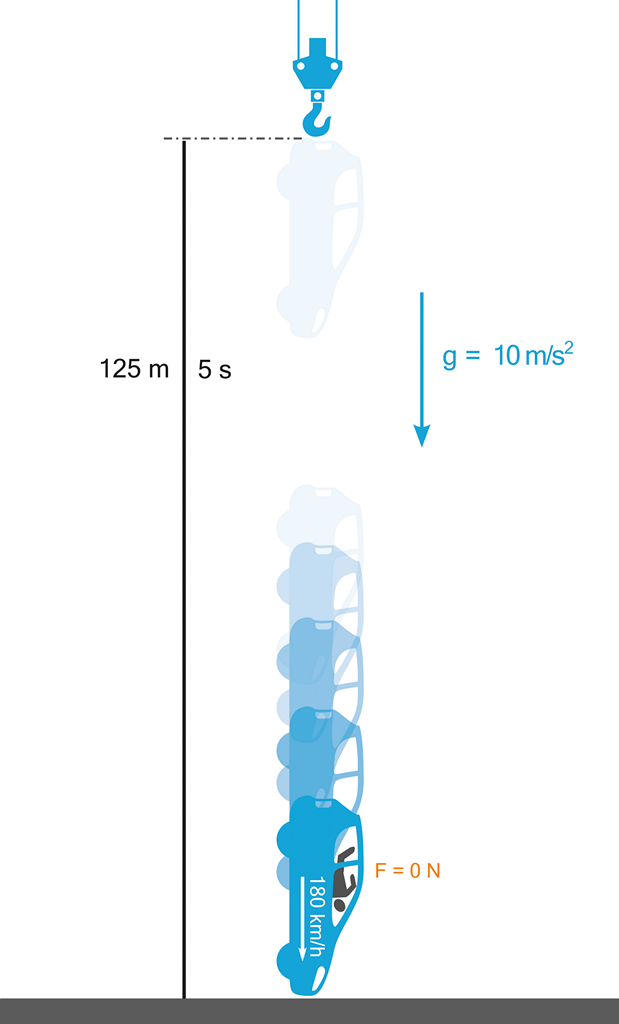
Obrázek 48:
Z nuly na 180 km/h za 5 sekund = velké zrychlení a NULOVÉ přetížení!
Je zde však jedna významná „anomálie“ při 2. scénáři:
Během tohoto zrychleného pohybu jezdec uvnitř vozu nepocítí naprosto žádnou sílu!
Posádka vozu (a všechny předměty ve voze spolu s ní) budou po dobu 5 sekund v beztížném stavu – ve stejném stavu, jaký zažívají kosmonauti na oběžné dráze! Stane se tak navzdory běžnému úsudku a navzdory fyzikálním „zákonům“, které jsme se všichni ve škole učili v souvislosti se jménem Isaaca Newtona!
Přestože půjde (z pohledu všech) o pohyb evidentně (velmi silně) zrychlovaný – na palubě padajícího vozu nikdo nezaznamená žádnou sílu, nepocítí žádné „zrychlení“ – pocit posádky i všechny měřicí přístroje ve voze budou hlásit „klid či rovnoměrný přímočarý pohyb“ – pouze pohled z okna vozu jim odhalí děsivou pravdu o zrychlujícím se pádu k Zemi!
Uspíme-li před experimentem posádku vozu (vzbudíme ji až v okamžiku startu) a vozu zatemníme okna – posádka automobilu bude přesvědčena, že je na oběžné dráze Země!
Po dobu oněch 5 sekund se budou všichni cítit jako v beztížném stavu vesmíru – hmotnost předmětů vymizí a jedním prstem půjde ze sedačky zvednout i předmět o hmotnosti 1000 kg. Vše, i voda (v podobě koulí), se bude volně vznášet v kabině. Nebude žádná síla, „vymizí“ gravitace!
Einstein ve svých úvahách dokonce tvrdí, že zavřeme-li skupinu těch nejlepších vědců se všemi moderními přístroji do uzavřeného modulu bez oken … nebudou schopni určit jaký je jejich „skutečný“ pohybový stav:
Zaznamenají-li vědci stav beztíže – nebudou umět rozhodnout, zda se nacházejí v hlubinách prázdného vesmíru, či zda se řítí volným pádem s rostoucí rychlostí směrem k Zemi.
Zaznamenají-li vědci pocit tíže (předměty budou silou přitlačovány k jedné straně modulu) – vědci nebudou umět rozhodnout, zda modul poklidně spočívá na Zemi díky gravitaci, či zda jej v prázdném vesmíru proudové motory urychlují s konstantním zrychlením do hlubin vesmíru.
V tomto ohledu budou Newtonovy zákony „zmatené“!
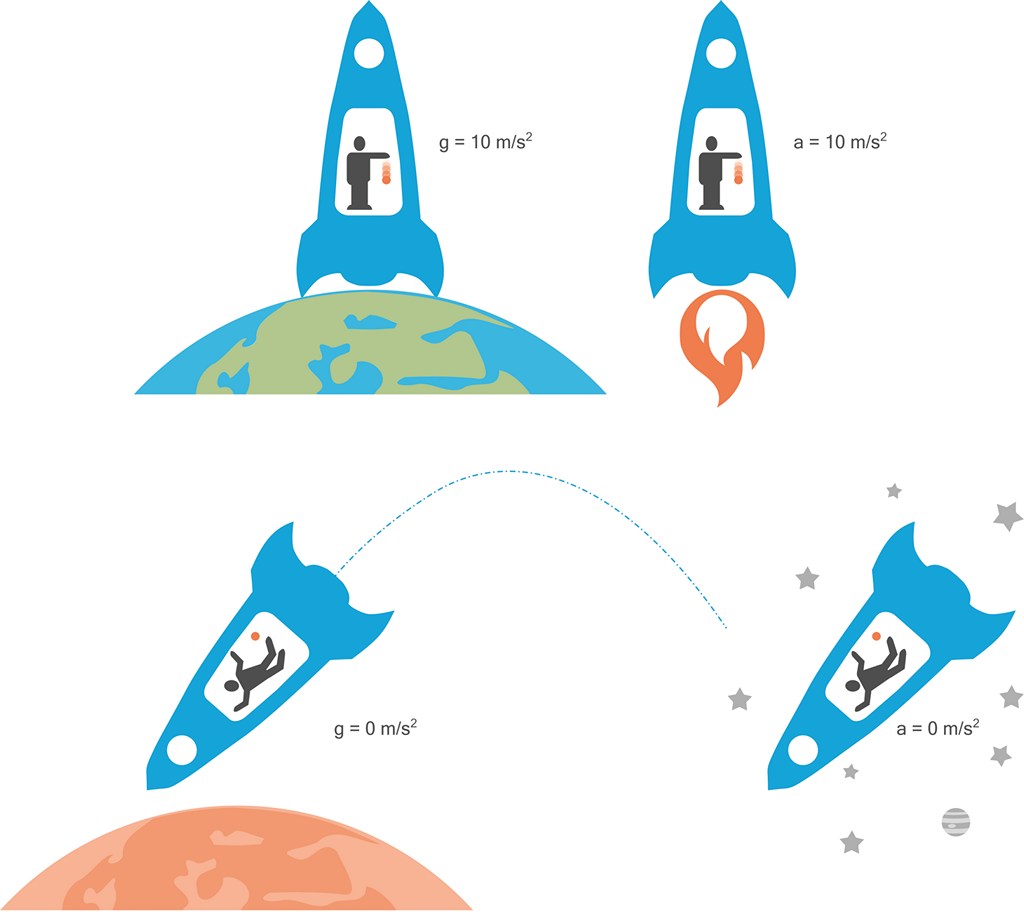
Obrázek 49:
Zmatek ve vědeckých hlavách: Kde jsem se to ocitnul?
Einstein byl prvním, kdo si uvědomil tento fenomén a „rozpolcenost“ klasické Newtonovské fyziky. Pochopil, že setrvačné a gravitační síly spolu souvisí nějakým naprosto fundamentálním způsobem a formuloval svou Obecnou teorii relativity (OTR), kterou se pokusil výšeuvedený fenomén objasnit.
Učinil tak (opět) zcela revolučním způsobem:
1.38.3.7 ZÁKLADNÍ PRINCIPY OTR
Obecnou TR Einstein publikoval v roce 1915 (s korekcemi v roce 1916) a postavil ji (znovu) na dvou postulátech:
1. Princip relativity – Fyzikální zákony ve všech vztažných soustavách jsou totožné a lze je vyjádřit stejnými rovnicemi.
2. Princip ekvivalence – Gravitační a setrvačné síly mají stejnou fyzikální podstatu.
Postuláty lze formulovat i poněkud „lidštějším“ způsobem:
1. Všechny děje dopadnou vždy stejně – bez ohledu na libovolný pohyb pozorovatele (laboratoře) – žádný pozorovatel není nijak privilegován.
2. Gravitaci a setrvačné děje od sebe nelze odlišit. Ve zrychlující kosmické raketě dochází ke stejným dějům (pocitům tíže) jako ve skutečném gravitačním poli. Naopak, na palubě volně padajícího letadla nastává stav beztíže a gravitační pole mizí.
Princip relativity zobecňuje (proto má tato teorie v názvu přívlastek „obecná“) princip formulovaný ve Speciální TR (známý de facto již od Galilea) na všechny pozorovatele – nejen pohybující se rovnoměrným přímočarým pohybem.
Einstein věděl, že u zrychlených (nerovnoměrných) pohybů lze snadno určit absolutní kritérium pohybu – fyzikální děje ve zrychlující se soustavě jsou specifické (ve zrychlujícím automobilu cítíte sílu tlačící vás do sedadla, stejně tak hladina vody ve sklenici přestane být „vodorovná“ a nakloní se ve směru zrychlení – při zpomalování tomu bude naopak). Toto jsou ona „absolutní“ hlediska, která umí rozhodnout, zda se pohybujete vy spolu s vlakem, či zda se pohybuje nádraží.
Einstein však trval na principu relativity a OTR formuloval takovým způsobem, že princip relativity zobecnil na jakékoliv pohybové děje, tedy i ty zrychlené. Naklonění hladiny vody ve sklenici může způsobit i gravitace nějakého dalšího masivního nebeského tělesa – ostatně, mořský příliv a odliv (mírné naklonění mořské hladiny) způsobuje gravitace Měsíce!
Dle Einsteina žádný absolutní pohyb neexistuje – nelze jej identifikovat ani u pohybů nerovnoměrných na základě působících setrvačných sil – stejné účinky totiž vyvolává gravitační pole – proto nikdy nelze odlišit, zda se pohybujete zrychleným pohybem, nebo stojíte v gravitačním poli.
Jakýkoliv pohyb je relativní!
Princip ekvivalence znamená nerozlišitelnost setrvačných a gravitačních jevů.
Einstein postuloval, že vše lze vysvětlit zakřivením prostoru + zakřivením času = zakřivením prostoročasu! Nebeská tělesa (Měsíc kolem Země, Země kolem Slunce, Sluneční soustava kolem centra galaxie, …) se pohybují na svých eliptických drahách spořádaně nikoliv proto, že jde o trajektorii, na které dochází k rovnovážnému stavu dvou sil (Newtonův pohled), ale proto, že tvar prostoru i času je v důsledku přítomné hmoty zakřiven takovým způsobem, jaký demonstruje výsledná eliptická trajektorie!
Zatímco mimo jakékoliv gravitační pole je trajektorií rovnoměrného přímočarého pohybu přímka, v blízkosti hmotných předmětů (a jejich gravitačního pole) je prostoročas zakřiven takovým způsobem, že trajektorií „rovnoměrného“ a „přímočarého“ pohybu je kružnice či elipsa (obecně: zakřivená přímka), na níž je trajektorie s měnící se prostorovou křivostí (kromě změny směru) „zakřivena“ též co do rychlosti pohybu!
Přestože se může zdát tato představa z počátku poněkud „šílená“, je v mnoha ohledech velmi logická a smysluplná – příběh o rovnoměrném přímočarém pohybu, probíhajícím proměnlivou rychlostí po elipse, dává totiž (navzdory terminologické schizofrenii) reálný smysl:
Vyšleme-li do vesmíru spící kosmonauty v raketě bez oken, nenajdou po probuzení (snadný) způsob, jak určit, zda jejich raketa letí rovnou trajektorií konstantní rychlostí v pustém vesmíru, nebo zda obíhá po kruhové dráze kolem Země – v obou případech nebudou na palubě lodi přítomny žádné síly, půjde o stav beztíže a „bezzrychlení“!
Podle Newtona je kruhová (mírně eliptická) trajektorie Země na cestě kolem Slunce dána rovnovážnou výslednicí gravitačních a setrvačných sil, stejně tak je dáno mírné zrychlování tohoto pohybu Země (v místech trajektorie Slunci nejblíže).
Podle Einsteina nejde o silové působení dvou rovnovážných sil – nejde o žádné síly – tvar trajektorie je přímým důsledkem zakřivení prostoru – pozorované kolísání rychlosti je přímých důsledkem zakřivení času – prostorová a časová trajektorie pohybu je přímým důsledkem zakřivení časoprostoru.
„Hmota říká časoprostoru, jakým způsobem se má zakřivovat; časoprostor říká hmotě, jakým způsobem se má pohybovat.“
Takovouto definicí lze podle Johna Archibalda Wheelera (přední americký astrofyzik, Princeton) nejstručněji shrnout Obecnou TR.
Einstein sám v tomto ohledu poznamenává:
„… prostoru a času nelze připisovat samostatnou existenci nezávisle na reálně existujících fyzikálních objektech …“
Několik dalších pokusů o formulování principů Obecné TR:
• Časoprostor je zakřivený: má neeuklidovskou geometrii (trojúhelník nemá součet úhlů 180°, rovnoběžky se sbíhají).
• Každé hmotné těleso zakřivuje prostor a čas kolem sebe (časoprostor) – čím hmotnější (těžší) těleso, tím větší zakřivení.
• Tělesa se pohybují po geodetikách (nejkratších možných drahách v zakřiveném časoprostoru). Zatímco na listu papíru je nejkratší dráhou přímka, na zakřiveném povrchu globusu vždy bude podobná „přímka“ zakřivená.
• Nejde o zakřivení trajektorie těles (pohled Newtonův), jde o zakřivení časoprostoru!
• Prostor a čas bez samotných těles neexistují. Tělesa sama časoprostor vytvářejí.
Zakřivení časoprostoru se v literatuře nejčastěji připodobňuje k trampolíně – použijme tedy také tuto analogii:
Umístíme-li těžký předmět (např. dělovou kouli) na trampolínu, vznikne prohlubeň. Obdobně zakřivuje přítomnost velkého množství hmoty ve svém okolí časoprostor. Čím hmotnější těleso, tím větší prohlubeň, respektive zakřivení časoprostoru. Pokud cvrnkneme „rovně“ po obvodu prohlubně ocelovou kuličku potřebnou rychlostí, bude krátce obíhat kolem dělové koule po kruhové dráze. Jde o analogii s obíháním planet kolem hvězd. Podobnou analogii nabízí i kulička vhozená do rulety v kasinu.
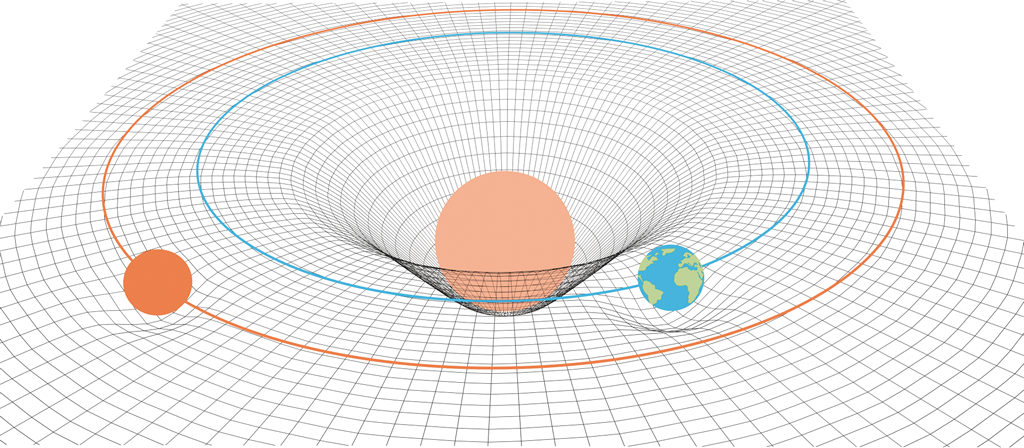
Obrázek 50:
Tradiční ztvárnění zakřiveného časoprostoru.
Znovu je nutné zdůraznit, že OTR neuvažuje s tradiční představou prostorového působení sil jako u Newtonovy teorie gravitace.
V OTR se hmotný bod pohybuje v prostoru rovnoměrným přímočarým pohybem po zakřivených geodetikách. Geodetika je termín označující nejkratší možnou spojnici v zakřiveném prostoru – ekvivalentní termínu „přímka“ v Euklidovském „rovném“ prostoru.
Protože je prostoročas zakřiven – jeví se trajektorie pohybu jako křivka prostorová (nerovná dráha) i křivka časová (zrychlování či zpomalování).
Externím pozorovatelem zaznamenaná křivka skokana do vody – zrychlený zakřivený pohyb – je pro skokana samotného (při zanedbání odporu vzduchu) beztížným stavem bez přítomnosti jakýchkoliv sil – tento atribut přitom odpovídá rovnoměrnému přímočarému pohybu!
Klasická fyzika měla s tímto jevem problém, OTR však podala (své) vysvětlení:
Není žádná přitažlivá síla Slunce, která by v rovnováze s odstředivou setrvačnou silou planet ve výsledku vykreslila eliptickou dráhu. Není přitažlivá síla Země, jež k sobě se vzrůstající rychlostí přitahuje padající předměty. Balistická dráha vystřelené dělové koule není výslednicí setrvačné síly dopředného pohybu a přitažlivé síly gravitace. Nejsou žádné síly!
Dle OTR všechny jmenované hmotné předměty deformovaly okolní čas i prostor takovým způsobem – že jejich pohybový stav je relativním klidem bez přítomnosti jakýchkoliv sil!
Nebeská tělesa se pohybují „rovnoměrným přímočarým“ pohybem ve zdeformovaném časoprostoru.
Matematický aparát OTR lokálně zakřivuje prostor a čas všech objektů ve vesmíru takovým způsobem, aby se všechny objekty mohly pohybovat prostorem „přímočaře“ a „rovnoměrně“ – po „přímkách“ vůči sobě navzájem.
Je zřejmé, že vytvořit matematickou konstrukci, která by toto dokázala, nebylo snadné!
Na tento úkol nestačily ani matematické znalosti Einsteina. Teprve za pomoci kolegů matematiků (během střídavých období optimismu a zklamání) dokázal Einstein matematicky formulovat svou teorii. Po několika letech usilovné práce, na podzim 1915, byla OTR představena světu, v roce 1916 prošla finální korekcí do své definitivní podoby.
Zakřivení časoprostoru v Riemannově geometrii vede v případě OTR k vysoce náročným matematickým postupům (přístupným málokomu). Matematici okolo Alberta Einsteina našli pro OTR exaktní popis principů teorie v podobě deseti diferenciálních rovnic druhého řádu (jde o velmi složitou matematiku).
První matematické řešení rovnic OTR pro sféricky symetrické gravitační pole centrálních těles (typicky jde o nebeská tělesa – planety, hvězdy, …) nalezl Karl Schwarzschild v roce 1916. Jeho řešení u „normálně“ silných gravitačních polí (naše Sluneční soustava) generuje pohybové trajektorie nebeských těles, které jsou téměř totožné s Newtonovými rovnicemi. V silnějších gravitačních polích (hmotnější hvězdy, neutronové hvězdy, …) se však OTR s Newtonovými predikcemi již rozchází, a to zcela zásadním způsobem:
Dle OTR se světelný paprsek v blízkosti silných gravitačních polí zakřivuje (ohýbá) silněji nežli dle Newtonových zákonů. Eliptické dráhy nebeských těles se více stáčejí (precese). Čas plyne v silnějším gravitačním poli pomaleji. Rozdílů je více …
Schwarzschildovo řešení OTR rovnic pro hmotná kulovitá tělesa (typické pro vesmírnou mechaniku) vedou k matematickému vztahu pro zpomalování času:
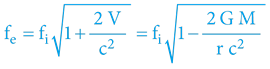 ; přičemž
; přičemž 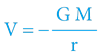
fefrekvence děje z pohledu externího pozorovatele dostatečně vzdáleného (limitně v nekonečnu)
fifrekvence děje z pohledu interního účastníka v gravitačním poli
Ggravitační konstanta (6,67·10‒11 N·m2·kg–2)
Mhmotnost tělesa generujícího gravitační pole
rvzdálenost od hmotného středu tělesa
crychlost světla
Vgravitační potenciál ve vzdálenosti r
V astrofyzikálním scénáři jde o to, že externí pozorovatel vně silného gravitačního pole bude pozorovat zpomalení všech dějů uvnitř oblasti se silným gravitačním polem (pozoruje zpomalenou frekvenci dějů), a naopak – interní pozorovatel uvnitř silného gravitačního pole bude pozorovat, že všechny vnější děje (mimo dosah gravitace, respektive jde o oblasti se slabším gravitačním potenciálem) jsou zrychlené (pozoruje zrychlenou frekvenci dějů).
Výšeuvedená rovnice gravitační dilatace času je dnes základem i pro objasnění „gravitačního rudého posuvu“ světla pozorovaného u vzdálených vesmírných objektů (frekvenční posun spektrálních čar). Protože pozorujeme vzdálené hvězdy či galaxie téměř z nekonečné vzdálenosti (gravitační potenciál pozorovaného objektu je na Zemi de facto nulový), je tedy zpomalena i frekvence pozorovaného světelného záření.
Všimněme si taktéž, že při určitém (dostatečně silném) gravitačním potenciálu vychází pod odmocninou výšeuvedeného vztahu nula, a to za situace:
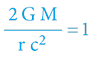
Pozorovaný objekt s takto limitně silným gravitačním potenciálem se bude jevit jako „zamrznutý v čase“ a navíc prakticky nepozorovatelný, neboť frekvence jeho světla se zpomalí na nulu a externí pozorovatel neuvidí vůbec nic. Objekty s ještě vyšším gravitačním potenciálem budou generovat pod odmocninou záporná čísla, což ve světě reálných čísel postrádá fyzikální intepretaci.
V našem vesmíru přitom nemusí jít o nikterak absurdně silná gravitační pole – představme si Slunce tisíckrát hmotnější a přitom s poloměrem Země – gravitační potenciál takovéhoto tělesa již povede k nulovým či záporným číslům pod výšeuvedenou odmocninou!
OTR a její matematický aparát jsou tudíž příčinou fenoménu s názvem Černá díra.
1.38.4 JE EINSTEIN JEDINÝM AUTOREM TEORIE RELATIVITY?
„Fantazie je důležitější než vědění.“
Albert Einstein
Ačkoliv jméno Albert Einstein je na celém světě synonymem pro Teorii relativity, bylo by historickým hříchem nezmínit Einsteinovy předchůdce či současníky, na „jejichž ramenou“ génius tohoto fyzika povstal.
Stěžejními myšlenkami, směřujícími k závěrům TR, se v Einsteinově době zabývalo několik vynikajících osobností tehdejší vědy a své teorie formulovali s Einsteinem paralelně, mnohdy dokonce i dříve! Einstein však prokázal (na rozdíl od ostatních) určitou „syntetickou“ schopnost – zakomponovat teorie jiných svých současníků do svého nového celku, a to vše navíc ve spojení se zvláštním nadáním Einsteinovy osoby pro popularizaci a „marketing“ svých teorií.
Kdo především inspiroval Alberta Einsteina či dubloval jeho teorie?
1.38.4.1 JOHANN GEORG VON SOLDNER
Johann Georg von Soldner byl německým fyzikem, astronomem a geodetem. V roce 1804 jako první usiloval o vypočtení ohybu světla v gravitačním poli Slunce. Při výpočtu vyšel z Newtonovy mechaniky a vypočetl ohyb paprsku světla při průletu kolem Slunce v hodnotě 0,84“.
Přesně k téže hodnotě došel i Einstein při svém prvním pokusu (1911) formulovat Obecnou TR. Později však Einstein své výpočty opravil a finální verze Obecné TR v roce 1916 již obsahovala rovnice, na jejichž základě vypočetl Einstein ohyb ve výši dvojnásobné (1,75“).
Přestože experimenty později potvrdily Einsteinův finální výpočet (jako jeden z „důkazů“ platnosti Obecné TR), práce Soldnera zůstává pozoruhodným počinem své doby.
1.38.4.2 ERNST MACH
Ernst Mach (1838‒1916) má české kořeny. Narodil se v Brně (Chrlice), část mládí prožil ve Zlíně, fyziku a psychologii studoval ve Vídni a později vědecky působil především v Praze. Jako téměř každý geniální fyzik (navíc český rodák) byl i muzikantem (hrál na varhany).
Přestože jeho jméno známe především v souvislosti s aerodynamikou (Machovou číslo označuje rychlost pohybu tělesa ve vztahu k rychlosti šíření zvuku), Ernst Mach ovlivnil významně i jiné oblasti fyziky:
Mach je považován za prvního „relativistu“, tento výraz však rozhodně nesmíme interpretovat jako příznivce Teorie relativity – spíše naopak!
Základním principem Machovy fyziky (i filosofie) bylo RELATIVIZOVAT svá poznání a zjištění z fyzikálních experimentů.
Mach byl prvním fyzikem, který upozorňoval na to, že Newtonova fyzika upřednostňuje „absolutno“ – pro Macha něco nepřijatelného. V roce 1883 vydal Mach svou legendární učebnici mechaniky, která si mimo jiné otevřeně „troufla“ napadnout základní Newtonovy principy – především princip absolutního (všudypřítomného) prostoru a času:
Newton zastával názor, že existence setrvačných sil umí „rozhodnout“ o tom, zda je pohyb relativní, či absolutní (zda se pohybuje vlak, či zda nádraží). Známý je především jeho experiment s rotujícím vědrem vody – hladina se prohne do tvaru hyperboly – tím Newton dokazuje absolutní objektivní pohyb kbelíku vůči „okolnímu“ absolutně klidnému „éteru“. Podle Newtona tento efekt nastane bez ohledu na okolí – i v prázdném vesmíru.
Mach však Newtonův argument zavrhuje. Odstředivý efekt hladiny vody v kbelíku vysvětluje jako důsledek relativního zrychlení obsahu kbelíku vůči souhrnnému gravitačnímu poli vesmíru. Podle Macha jsou všechny dynamické děje ve vesmíru – setrvačnost těles i Newtonem popsané pohybové zákony – důsledkem působení okolních těles vesmíru. V prázdném vesmíru by dle Macha setrvačnost ani gravitace (tedy hmotnost) neexistovaly.
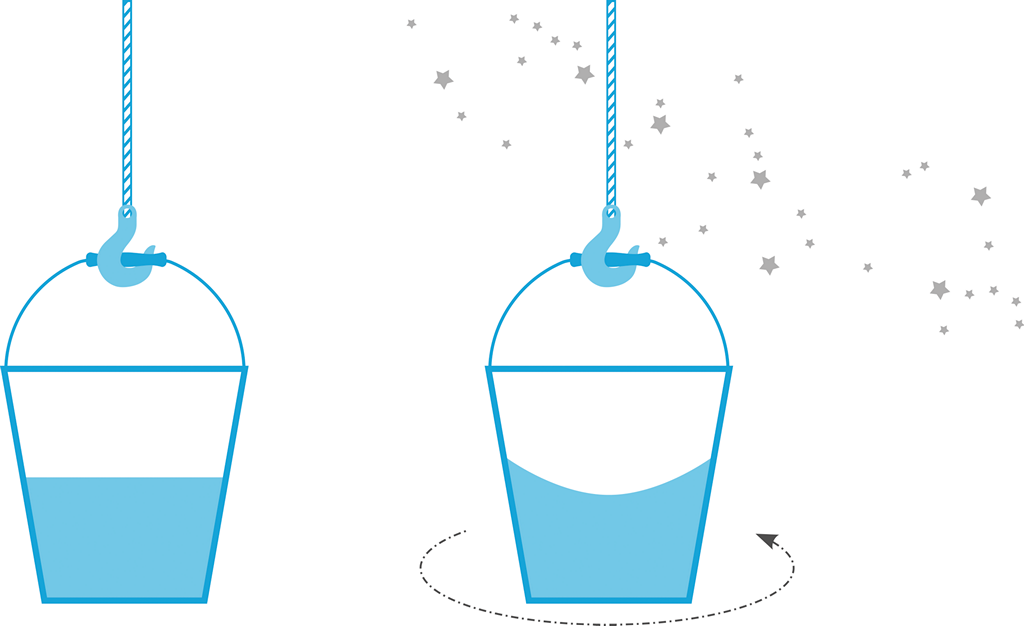
Obrázek 51:
Veledůležitý argument pana Newtona.
Machův princip vychází z představy, že lokální fyzikální zákony (tak jak jsou v daném místě vesmíru popisovány) mají svůj původ v globálních parametrech vesmíru jako celku, respektive – lokální fyzikální zákony jsou ovlivňovány celkovým rozložením hmoty ve vesmíru.
Při své kritice Newtonovy koncepce (absolutního prostoru a času) vyjádřil Mach myšlenky, které (spolu s idejemi neeukleidovské geometrie) hrály významnou úlohu pro Einsteina při tvorbě principiálních základů jeho OTR.
Právě na základě Machova vidění světa začal mladý Albert Einstein stavět svou Teorii relativity. Mladý vědec se dlouho považoval za následovníka Machova učení, a byl proto pochopitelně zklamán, když se Mach stavěl velmi rezervovaně k Teorii relativity poté, co byla Einsteinem publikována.
Mach se až do konce života nedokázal smířit s TR a snažil se dokázat principiální nedostatky této teorie – teorii označoval za „dogmatickou“ či „paradoxní nesmysl“. Einstein na oplátku přestal glorifikovat svého učitele a občas haněl jeho názory na fyziku i filosofii.
1.38.4.3 JAMES CLERK MAXWELL
Einstein vystavěl svou teorii mimo jiné i na pochopení podstaty elektromagnetického záření (na konstantní rychlosti světla). V Maxwellových rovnicích je rychlost světla determinována pouze elektromagnetickými vlastnostmi vakua (permitivita, permeabilita) – rychlost pohybu zdroje světla v těchto rovnicích vůbec nefiguruje a tento fakt byl pro Einsteina zcela jistě velmi dobrou „nápovědou“.
Bez Maxwellovy práce by Einsteinova teorie pravděpodobně nikdy nevznikla.
Paradoxem zůstává, že Maxwell byl po celý život fundamentálním zastáncem existence všudypřítomného éteru (jímž se světlo šíří), a právě Einstein svou teorii založil na myšlence, že éter neexistuje!
1.38.4.4 WOLDEMAR VOIGT
Německý fyzik jako první (1887) použil matematický vztah, který později vstoupil ve známost jako „Lorentzův faktor“ (ano – je to poněkud nelogické a nespravedlivé):
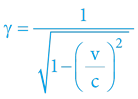
Voigtova transformace usilovala o vysvětlení Dopplerova efektu v dokonale rigidním (nestlačitelném) médiu a mimo jiné byla též „lékem“ na výsledky Michelson/Morley experimentu.
Voight ve své práci odvodil dilataci času a byl jejím zastáncem. Nikterak však nepracoval s kontrakcí délek (na rozdíl od svých následovníků).
Jeho práce však byla odbornými kruhy v té době téměř ignorována. Až pozdější velikáni (Minkowski například) složili hold jeho práci a zásluhám.
1.38.4.5 HENDRIK LORENTZ
Vynikající holandský fyzik a nositel Nobelovy ceny taktéž usiloval o vysvětlení Michelson/Morley experimentu. V letech 1892‒1904 přišel Lorentz se svými matematickými vztahy.
Lorentz formuluje (nezávisle na Voightovi) své matematické transformace a z nich vyvozuje nejprve kontrakci délek a o něco později i dilataci času (byť této časové anomálii přikládá pouze „pomocný“ matematický význam, a nikoliv význam fyzikální).
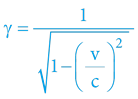
Ačkoliv se ani Lorentz nikdy zcela nevzdal myšlenky existence univerzálního éteru, podporoval teorii Alberta Einsteina, který svou práci postavil mimo jiné i na Lorentzově matematickém aparátu (Lorentzova transformace). Po určitou část historie proto byla Einsteinova STR často nazývána jako Einstein-Lorentzova teorie.
1.38.4.6 J. J. THOMSON, WILHEM WEIN, WALTER KAUFMANN
Britský fyzik a nositel Nobelovy ceny J. J. Thomson již v roce 1881 zaregistroval, že částice s větší energií se jeví hmotnější.
Wilhem Wien ve své práci v roce 1900 usiluje o kvantifikaci vztahu hmotnosti a energie a přichází se vztahem E = ¾ m c2, což byl sice vztah nepřesný, nicméně kvalitativně již velmi blízký realitě.
Až Walter Kaufmann na základě svých experimentů (1901‒1903) přichází s interpretací, která je rovnocenná vztahu E = m c2.
1.38.4.7 HENRI POINCARÉ
Henri Poincaré byl francouzský matematik, fyzik a filosof, který mimo jiné položil i základy teorie chaosu či topologie (matematické vyjádření vlastností prostoru).
Poincaré došel ve své práci k podobným závěrům jako Einsteinova STR. Poincaré (nezávisle na práci Alberta Einsteina) již v roce 1900 formuloval „princip relativity“ (prvně popsaný Galileem).
Poincaré v roce 1905 (několik měsíců před Einsteinem) odvodil většinu matematických vztahů a důsledků jako Albert Einstein – používaje a odvolávaje se na Lorentzovu transformaci jako na základní matematický aparát.
Poincaré také jako první začal pohlížet na prostor jako čtyřrozměrnou veličinu (kde je čtvrtým rozměrem čas). Jeho myšlenky však dovedl do celistvé teorie až Minkowski:
1.38.4.8 HERMANN MINKOWSKI
Hermann Minkowski vnesl do fyziky jako první myšlenku propojeného časoprostoru (1907). Bez tohoto syntetického a revolučního pohledu na reálnou existenci časoprostoru (onu bipolární jednotu času a prostoru) by nikdy nevznikla OTR (1916), neboť tato teorie je (stručně řečeno) teorií o zakřiveném časoprostoru.
V Einsteinově předchozí práci – STR (1905) – není o časoprostoru ani zmínka, STR pohlíží na čas i prostor stále ještě jako na nezávislé oddělené veličiny!
Teprve v roce 1912, při tvorbě OTR, mluví Einstein poprvé o čase jako o čtvrtém rozměru všeobjímajícího časoprostoru. Bez geniálního přínosu Hermanna Minkowského by OTR nikdy nevznikla.
1.38.4.9 MILEVA MARIC-EINSTEIN
Mileva Maric (1875‒1948) byla první manželkou Alberta Einsteina.
Ačkoliv mnozí historici povšechně opomíjejí její jméno, jiní naopak připisují této Einsteinově družce stěžejní podíl na vědeckých úspěších jejího muže:
Mileva byla jako vzdělaná a nadějná Srbka jednou z mála žen, kterým bylo dovoleno studovat na univerzitě polytechniky v Curychu. Ve stejném ročníku s Einsteinem byla vůbec jedinou ženou. Během studií vykazuje Mileva ve fyzice stejně dobré výsledky jako Albert Einstein. Při studiích se mladý pár seznamuje a oba spolu vášnivě debatují o některých fyzikálních problémech. Vášeň následně přeroste i mimo oblast fyziky.
Mileva měla nejspíš přirozenou slabost pro geniální muže – ještě před Einsteinem byla za studií přítelkyní svého krajana Nikola Tesly. Bez tohoto génia by nevznikla přenosová elektrická soustava, točivé elektromagnetické pole by neroztáčelo motory strojů a bezdrátový přenos rádia či televize bychom také neměli – průmyslová revoluce by se nekonala.
Mileva, přes svoji zálibu ve fyzice a matematice, studia nedokončila – v té době (1902) již čekala s Einsteinem „nemanželské“ dítě – dceru Lieserl. Historici dodnes přesně netuší následný osud narozeného dítěte (neví se, zda zemřelo, či bylo dáno k adopci). Zatímco Einstein tuto událost vytěsňuje ze své mysli, Milevu traumatizuje po zbytek života.
• V roce 1903 dojde ke sňatku a hned následující rok se páru narodí (již manželský) syn Hans Albert.
• V roce 1905 publikuje Albert první revoluční práci – Speciální teorie relativity. Vášnivý manželský i vědecký vztah nadále funguje a v roce 1910 se rodí druhý syn Eduard.
• V roce 1912 Einstein poprvé mluví o čase jako čtvrtém rozměru časoprostoru a pracuje s touto myšlenkou na formulaci Obecné TR. Zároveň se však začínají projevovat v manželství velké problémy, Albert se seznamuje se svou rozvedenou sestřenicí Elsou Löwenthalovou, s níž si vyměňuje milostné dopisy (později ji pojme za svou choť).
• V roce 1914 již Mileva odmítá následovat Alberta do nového působiště.
• V roce 1915 je Obecná TR publikována.
• Únor 1919 je datem rozvodu a v červnu si Albert bere svou druhou ženu – sestřenici Elsu Löwenthalovou.
Od této doby již Einstein nevytvoří žádnou obecně přijímanou fyzikální teorii. Jeho následné pokusy o nalezení „Unitární teorie pole“ zůstanou až do konce jeho života neúspěšné. Všechny veliké vědecké úspěchy Alberta Einsteina se tak udály během jeho manželství s první ženou Milevou Maric.
Mnoho historických pramenů, svědectví i vyjádření samotného Alberta Einsteina dokládají, že Mileva Maric byla pro Alberta podporou a pomocníkem nejen v domácnosti. Myšlenky i debaty nad TR a jejími principy sdíleli oba manželé spolu – o tomto faktu existují historické důkazy.
Vzhledem k „historické roli“ žen v dané době se nelze divit, že veškerý úspěch a slávu přisuzují dějepisci pouze Albertu Einsteinovi. Dnes již můžeme pouze spekulovat, jak veliký byl myšlenkový vklad první Einsteinovy manželky. V každém případě by však bylo nespravedlivé, vůči Milevě Maric, ignorovat její jméno a její možný vědecký přínos.
1.38.4.10 … A MNOHO DALŠÍCH
Výšeuvedený výčet jmen Einsteinových předchůdců není zdaleka úplný. Zájemci o hlubší vhled do této problematiky by neměli opomenout především jména:
Nikolay Umov, Olinto De Pretto, William Crookes, Friedrich Hasenöhrl, August Föppl, Joseph Larmor, Emil Cohn, George Fitzgerald.
Ani tento výčet není úplný …
1.38.4.11 EINSTEIN – MARKETINGOVÝ STRATÉG
Přestože někteří historici (vzhledem k výšeuvedenému) zpochybňují Einsteinovo prvenství a nebojí se Einsteina dokonce obviňovat i z plagiátorství – nesporným faktem zůstává, že ať již Einstein ve svých názorech vycházel z myšlenek kohokoliv – on byl prvním a jediným, kdo dokázal svou teorii „prodat“ nejen odborné veřejnosti, ale i vznikajícím masmédiím, respektive široké laické veřejnosti.
Spojení „bláznivé“ teorie a dostatečně „podivínského“ génia – ústící v představu, že čas i prostor kolem nás lze nějak deformovat a možná i cestovat časem – to vše udělalo z Einsteina během krátké doby hvězdu první velikosti nejen na poli vědeckém, ale i společenském a politickém.
Od učebnic fyziky (a společenského povědomí) nesmí žádný vědec čekat absolutní spravedlnost. I historická fakta mohou být „relativní“!
Přestože je TR objektivní optikou spíše „kolektivním dílem“ více autorů, nesmrtelnost tato teorie zajistila pouze jménu Albert Einstein!
Kromě Teorie relativity – se kterou je Albert Einstein nejčastěji spojován – nesmíme zapomenout ani na další objevy tohoto génia – především na objasnění Fotoelektrického jevu, kterým Einstein poprvé popsal dualitu světla, respektive jeho vlnově-částicový charakter.
Ve sporu Newtona s Hookem (a Huygensem) – o principiální povahu světla – tedy měli pravdu všichni zúčastnění!

