NEKONZISTENTNÍ POCHOPENÍ ČASOPROSTORU

Ačkoliv je Einstein dnes často chápán a interpretován jako „vynálezce“ časoprostoru, který prvně pochopil provázanost těchto dvou základních veličin fyziky … jde o omyl. Prvenství patří jinému velikánovi teoretické fyziky – sám Einstein dokonce myšlenku časoprostoru několik let haněl!

Z historických pramenů nalézáme již u Inků (a příbuzných národů v Andách), že významové kategorie „prostor“ a „čas“ vnímali jako jeden pojem a vyjadřovali je jedním slovem.

Německý filosof Arthur Schopenhauer popsal v roce 1813 myšlenku, že filosofické kategorie čas a prostor samy o sobě neodpovídají povaze světa, že teprve jejich syntetické spojení umožňuje existenci věcí.

Edgar Allan Poe vyjádřil ve své knize Eureka (1848), že:

„Prostor a trvání jedno jest.“

Roku 1895 publikoval H. G. Wells ve známé novele The Time Machine, že:

„Není žádného rozdílu mezi časem a jednotlivými třemi rozměry prostoru kromě toho, že se naše vědomí spolu s časem pohybuje … každá reálná věc se rozprostírá ve čtyřech dimenzích: musí mít délku, šířku, tloušťku a trvání.“

Všem předchozím myšlenkám dal však exaktní popis až Hermann Minkowski – to on je právoplatným objevitelem existence a duality časoprostoru (1907)!

Tento (téměř zapomenutý) génius jako první odhalil, že matematické vztahy známé jako Lorentzovy transformace (1899), s jejichž pomocí Einstein vybudoval svou Speciální TR (1905), jsou jen matematickým vyjádřením geometrické provázanosti prostoru a času.

V roce 1907 Minkowski stvořil ve své práci čtyřrozměrnou geometrii časoprostoru (Zeit-Raum), kdy k běžnému Euklidovskému 3dimenzionálnímu světu přidáme čtvrtý časový rozměr, v němž se časová osa „pohybuje“ rychlostí „c“ (rychlost světla).

2.2.1 MINKOWSKI A EINSTEIN

Vztah obou géniů byl poněkud problematický:

Minkowski byl Einsteinovým profesorem matematiky a mechaniky na studiích v Curychu. Einstein, nicméně, přednášky Minkowského příliš poctivě nenavštěvoval (obzvláště ty matematické), a proto byl Minkowski roku 1905 příjemně překvapen revolučními myšlenkami Speciální TR svého nevýrazného studenta.

Pro Einsteina bylo naopak nepřijatelné, když v roce 1907 Minkowski přetransformoval jeho STR do jakési geometrie ve čtyřrozměrném časoprostoru. Minkowského teorii časoprostoru Einstein proto několik let odmítal a tituloval jako: „nadbytečná erudice … od té doby, co se matematici vrhli na moji teorii, přestávám rozumět sám sobě … stěží pochopitelné“.

Einstein byl teoretický fyzik – excelující ve fyzikálních imaginacích a „myšlenkových experimentech“. Matematické výpočty a matematika obecně však byly pro Einsteina „nutné zlo“ – právě proto se Einstein rád obklopoval brilantními matematiky, kteří mu pomáhali matematicky formulovat jeho fyzikální myšlenky.

Možná z tohoto důvodu Einstein zpočátku neprohlédl genialitu Minkowského 4D světa a jeho „vnitřní krásu“.

V lednu 1909 však Hermann Minkowski náhle umírá (ve věku pouhých 45 let) a bohužel se nedožije satisfakce, když Einstein (a spolu s ním celá moderní fyzika) zavrhnou dosud oddělovaný čas a prostor, přijímajíce jednou provždy duální časoprostor (4D svět).

Postupem času Einstein (s prací na OTR) docenil význam Minkowského 4D prostoru, neboť právě zakřivením časoprostoru bylo možno „elegantně“ vysvětlit gravitaci.

V roce 1912 již Einstein mluví o čase jako o čtvrtém rozměru 4D kontinua. V roce 1916 pak představuje svou Obecnou TR jako zcela nový pohled na zakřivené prostoročasové kontinuum. V jedné z prvních prezentací OTR – Einstein s určitou zdrženlivostí uznal, že jeho objev byl „velmi usnadněn“ Minkowského pojetím STR.

V oblasti geometrie 4D prostoru dal Einstein Minkowskému nejen zapravdu – Einstein svého učitele „překonal“:

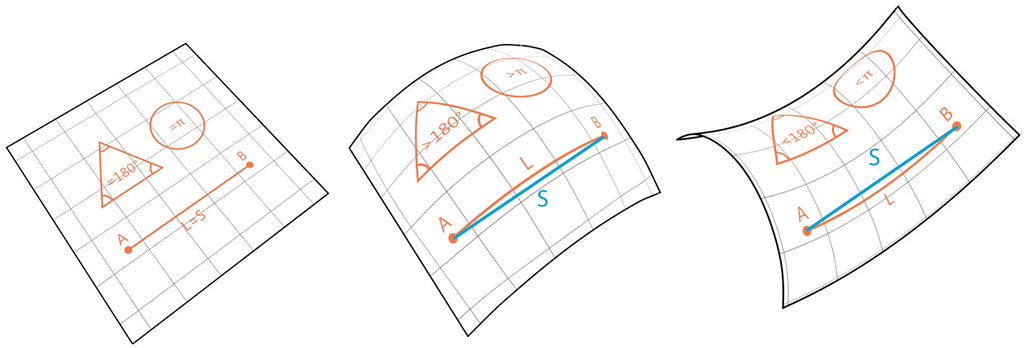
Minkowski totiž svůj 4D prostor myšlenkově i matematicky vybudoval v oblasti Euklidovské geometrie – v onom „normálním“ světě, kde platí Pythagorova věta, součet úhlů v trojúhelníku je 180° a rovnoběžky jsou rovnoběžkami.

Einstein však chtěl svojí Obecnou TR objasnit podstatu gravitace – objasnit zakřivované trajektorie pohybu těles, samovolně zrychlující se „pád“ … a proto transformoval Minkowského 4D svět do Riemannovy geometrie, která je (zjednodušeně řečeno) v každém svém bodě libovolně zakřivená, rovnoběžky se zde sbíhají a trojúhelníky mají různé součty úhlů.

V obecně zakřiveném světě lze poměrně snadno filosoficky i fyzikálně „vysvětlit“ jakýkoliv pohyb a jakoukoliv trajektorii. Ať již zaznamenáte libovolně nepravidelný pohyb v prostoru – měnící směr či měnící rychlost – vždy dokážete dopočítat natolik specifickou geometrii časoprostoru, aby vysvětlovala pohybovou trajektorii. Jde o „univerzální řešení“ všech pohybových dějů:

Trajektorie letu skokana na lyžích (na zimní olympiádě) je pouhým projevem zakřivení časoprostoru. Neexistují žádné síly – ani gravitační síla, ani odstředivá síla, ani setrvačná síla – vše je jen zdánlivé a skutečnou podstatou výsledné trajektorie je specifické zakřivení časoprostoru.

Přestože OTR vychází z jednoduché myšlenky (člověk padající volným pádem ztrácí vlastní váhu a zažívá stav beztíže), Einstein tento rozpor vůči Newtonovské fyzice „narovnává“ pokřivením prostoročasu a velmi složitou matematikou: Používá obecnou deformaci těch nejzákladnějších atributů fyziky – lokálně specifické zakřivení času a prostoru (časoprostoru).

Brilantní … ale není to příliš?

• Až do začátku 20. století žilo lidstvo v představě 3D světa, který sestával ze tří na sebe kolmých rozměrů – v „rovném“ světě, kde se můžete spolehnout na Pythagorovu větu a rovnoběžky, jež se nikdy neprotnou. Právě na tomto základě jsme zmapovali veškerý svět kolem nás i okolní vesmír!

• V roce 1905 formuloval Einstein svou STR – založenou na matematice pravoúhlého trojúhelníku.

• V roce 1907 Minkowski popsal existenci časoprostoru – v němž je čas dalším (čtvrtým) prostorem – kolmým ke všem třem primárním prostorovým rozměrům.

Fundamentem takovéhoto časoprostoru je tudíž platnost Pythagorovy věty (matematika pravoúhlého trojúhelníka ≈ kolmost čtvrtého prostoru). Fyzikální i matematický aparát STR tak Minkowski odůvodnil jediným postulátem – existencí časoprostoru!

• V následujících letech Einstein s Minkowského časoprostorem nesouhlasí.

• V roce 1916 Einstein přichází se svou OTR. Fundamentem je Minkowského časoprostor, který je však transformován do obecně zakřivené Riemannovské geometrie, kde Pythagorova věta neplatí a pravé úhly již nejsou pravé.

Jaké jsou tedy (vlastně) fundamentální principy Teorie relativity?

Jaký je její myšlenkový základ?

A kde je ona deklarovaná vnitřní krása?