3.6.9 GRAVITAČNÍ RUDÝ POSUV
V kapitole Pound-Rebka experiment jsme již prokázali, že gravitační rudý posuv (dále i GRP) elektromagnetického záření v homogenním gravitačním poli Země lze spočítat mnohem jednodušší matematikou, nežli nám podsouvá OTR, a to čistě na základě Newtonovské fyziky – v kombinaci se znalostí Planckovy konstanty a úměrnosti hmotnosti a energie E = m c2.
Upozornili jsme taktéž, že výpočet GRP byl v dané kapitole limitován pouze na rámec homogenního (konstantního) gravitačního pole (na zemském povrchu lze za homogenní pole považovat výškový rozdíl do řádu maximálně stovek metrů). Stejně tak jsme v onom výpočtu nekalkulovali se skutečností, že každý foton při stoupání v gravitačním poli nutně „platí“ účet za potenciální energii (kterou stoupáním získává) svou vlastní energií, respektive svou vlastní hmotností (dle E = m c2), respektive svou vlastní frekvencí a vlnovou délkou (dle Planckovy konstanty).
Zatímco míč vykopnutý do výšky může „platit“ gravitačnímu potenciálu Země účet svou kinetickou energií (postupně zpomaluje, následně se vydá na cestu zpět) – foton zpomalovat nemůže – nemůže platit svou kinetickou energií – musí platit svou primární energií, respektive svou hmotností, respektive snížením své frekvence.
Chceme-li odvodit korektní a obecný vzorec pro GRP, který nebude platit pouze v homogenním poli, nýbrž i v poli radiálně klesajícím – obecná filosofie výpočtu (zákon zachování energie) bude totožná, pouze musíme „posčítat“ danou úlohu pro jednotlivé (dostatečně malé) úseky dráhy, respektive musíme použít integrální počet.
Není cílem této knihy strašit čtenáře složitější matematikou, a tak se pouze omezíme na konstatování:
Úloha vede k diferenciální rovnici:
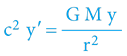
Ggravitační konstanta
Mhmotnost hvězdy (planety)
rradiální vzdálenost od středu hvězdy (planety)
yhledaná matematická funkce (y´ je derivací hledané funkce)
crychlost světla
Připomínáme, že TČ definuje množství hmoty primárně pojmem energie E (kg) namísto tradičního pojmu hmotnost (M)! Kvůli porovnání s TR však tentokrát TČ řeší úlohu v tradičních jednotkách SI:
Řešením diferenciální rovnice získáme výsledný vztah:
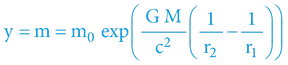
Označujeme-li gravitační potenciál vztahem …
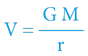
… je ekvivalentním vyjádřením rovnice:
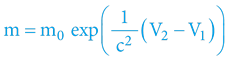
V1gravitační potenciál hvězdy v místě vzniku daného záření na vzdálené hvězdě
V2gravitační potenciál hvězdy v místě pozorování (zpravidla na Zemi)
V astronomii je většinou kalkulován GRP z velmi vzdálených zdrojů, gravitační potenciál (V2) vzdálené hvězdy je tudíž „v cíli“ de facto nulový V2 = 1/∞ ≈ 0, a vztah tedy přejde do jednodušší podoby:

A protože je hmotnost fotonu přímo úměrná jeho frekvenci, je finální vzorec GRP (pro danou situaci):
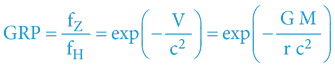
Pro zajímavost – „obrácený“ vztah pro gravitační modrý posuv (GMP), tedy scénář, kdy „ufouni“ na vzdálené hvězdě měří nárůst energie záření Země – je vztah analogický:
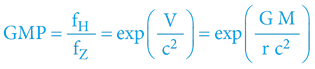
Samozřejmě zde totiž platí, že:
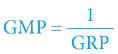
Vgravitační potenciál v místě vzniku daného záření na vzdálené hvězdě (V = V1)
expexponenciální funkce ex
fZfrekvence záření na Zemi
fHfrekvence záření na vzdálené hvězdě
Ggravitační konstanta
Mhmotnost tělesa, z něhož světelné záření pochází
rvzdálenost od povrchu hvězdy (místa, kde vzniklo dané záření) k jejímu středu (zpravidla tedy jde o poloměr hvězdy)
Finální matematický vzorec nám sděluje, že GRP je přímo definován exponenciálou gravitačního potenciálu (faktor c2 ve jmenovateli lze snadno eliminovat rozumnější definicí jednotky hmotnosti, respektive energie – viz dále).
Samotná exponenciální funkce je v matematice veledůležitou a bazální funkcí (podobně jako funkce trigonometrické). Všechny tyto funkce jsou de facto „příbuznými“ ze stejné rodiny funkcí. Sinus a cosinus jsou obě řešením diferenciální rovnice y´´ = −y; přičemž exponenciální funkce je řešením diferenciální rovnice y´ = y. Výjimečnost exponenciální funkce spočívá mimo jiné i v tom, že její derivace je totožná funkci samotné!
Na exponenciální funkci (respektive jí inverzní logaritmickou funkci) jsme již narazili v kapitole Cestování ke hvězdám, kde jsme poznali funkci arcsinh (inverzní hyperbolická funkce je definována právě pomocí logaritmů).
Pro úplnost dodejme, že výšeuvedené vztahy TČ neobjevila, nýbrž znovuobjevila:
Jako první je publikoval finský fyzik Gunnar Nordström (1881‒1923), nicméně jeho fyzikální myšlenky ve své době soupeřily s Teorií relativity, která získala mnohem více příznivců – spolu s Nordströmem tak upadly v zapomnění i jeho vztahy pro výpočet GRP.
Bez ohledu na skutečnost, kdo výšeuvedené vztahy objevil jako první – jde o jediný korektní výpočet GRP!
OTR pro stejnou fyzikální situaci používá rovnici:
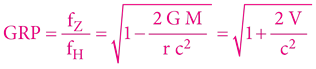
… kde používáme „tradiční“ záporný tvar pro výpočet gravitačního potenciálu:
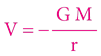
Na základě tohoto vztahu se odehrál třetí ze slavných „důkazů“ platnosti TR:
Einsteinův „dvorní astronom“ Eddington (ten, který „potvrdil“ relativistický ohyb světla v gravitačním poli Slunce) sekundoval Adamsovi (americký astronom), který v roce 1925 spočítal GRP Siria B (menší část dvojhvězdy Sirius).
Co dodat?
Dosadíme-li známé fyzikální charakteristiky Siria B (hmotnost, poloměr) do obou vzorců (TČ vs. OTR) – výsledky jsou prakticky totožné:
Dle TČ (a Nordströma) činí poměrné posunutí frekvence: 2,608·10‒4
Dle OTR činí poměrné posunutí frekvence: 2,609·10‒4
Oba výpočty jsou v souladu s experimentem – naměřeným posunem (na různých spektrálních čarách).
Jinými slovy:
V „blízkém“ vesmíru, kde dokážeme (snad) s relativně malou chybou (na základě Newtonovy gravitace!) určit hmotnost nebeských těles a kde jsou hodnoty gravitačního potenciálu relativně malé (na rozdíl od center galaxií) – jsou oba matematické vzorce ekvivalentní a dávají zcela shodné výsledky (rozdíl je menší nežli chyba experimentu).
Blízký vesmír tak popisují oba vztahy zcela rovnocenně!
Stejně tak jako v případě Pound-Rebka experiment – lze pozorované jevy zcela srovnatelně objasnit buď na základě (komplikované) Einsteinovy OTR, anebo na základě (jednodušší) Newtonovy fyziky a TČ.
Co když ale zamíříme svoji pozornost (a teleskopy) do vzdálenějšího vesmíru, kde existují hmotnější tělesa a mnohem vyšší gravitační potenciál? Když pohlédneme dále nežli na pouhou periferii naší galaxie (k Siriu letí světlo necelých 9 let, zatímco do centra galaxie přes 27 000 let)? Budou i pak obě teorie rovnocenné?
Na tuto otázku odpoví následující kapitola:

