3.4.2 KOMENTÁŘ K ZÁKONU
Přestože je „čas“ pro každého velmi abstraktní kategorií, je zcela konkrétní součástí našeho světa a našich životů. Navzdory veškerému lidskému vědění (i navzdory této knize) se musíme smířit s tím, že přesná a exaktní představa o podstatě času nám zůstává utajena. Nicméně – na jednu otázku možná dokážeme odpovědět již dnes:
Jakou rychlostí a jakým směrem „letí“ čas?
Šíří se událost prostorem konečnou, či nekonečnou rychlostí?
Projeví se událost v jedné části vesmíru současně i ve všech ostatních oblastech vesmíru?
Je moje „teď“ současné jako „teď“ kohokoliv jiného?
Je zde několik indicií, které naznačují, že čas (událost) prostorem „letí“ rychlostí omezenou, že čas se nešíří „okamžitě“:
Dodnes například nikdo nepřišel na to, jak odstranit prodlevu v komunikaci kosmonautů na Měsíci s řídicím střediskem Země. Když kosmonaut vysloví svůj pozdrav „Hi“ do mikrofonu, nikdy nedostane odpověď ze Země za dříve nežli 2,5 vteřiny! Stejně tak počítač kosmonautů, odesílající data na Zemi, nedostane odpověď od řídicího serveru dříve nežli za ony 2,5 vteřiny.
Hledíme-li na Měsíc, pozorujeme historii starou cca 1,25 vteřiny. V případě Slunce jde o historii starou 8 minut. U nejbližších hvězd vidíme historii před 4 lety a záření jiných galaxií dopadající do našich očí je „staré“ i několik miliard let!
Výšeuvedené skutečnosti jsou známé fyzikům již od konce 19. století. Všichni však toto zpoždění dávali „za vinu“ omezené rychlosti šíření světla – nenašli jsme žádnou jinou formu hmoty, jež by se vesmírem šířila rychleji. Světlo (respektive elektromagnetické vlnění) se z našeho externího pozorovatelského hlediska jeví, jako by mělo nastavený „omezovač“ rychlosti na hodnotu 300 000 km/s (299 792 458 m/s).
Fyzikální pokusy na konci 19. století, ve snaze popsat vlastnosti hypotetického éteru (média, v němž se má světlo šířit), dávaly výsledky naznačující, že světlo se onou stejnou konstantní rychlostí šíří bez ohledu na to, zda mu letíme vstříc, či naopak.
Ani génius Alberta Einsteina neodpověděl na otázku, proč se světlo chová tak abnormálně. Einstein však namísto odpovědi použil tento fenomén jako druhý postulát své STR (Rychlost světla ve vakuu je pro všechny pozorovatele v inerciálních vztažných soustavách stejná, a to ve všech směrech – nezávisí na rychlosti objektu vyzařujícího světlo).
Teprve Hermann Minkowski si povšiml, že zdánlivou anomálii absolutní rychlosti šíření světla v prostoru lze vysvětlit tím, že čas (událost) se šíří prostorem zcela konkrétním a specifickým způsobem. Tento geniální fyzik (který bohužel zemřel příliš mlád) se jako první vážně zabýval myšlenkou, že podivné chování světla je pouhým důsledkem něčeho „hlubšího“ – důsledkem toho, jakým způsobem se šíří prostorem čas!
V minulých staletích jsme pronikli hluboko v poznání téměř všech fyzikálních kategorií – obří teleskopy zmapovaly okolní vesmír, téměř známe strukturu hmoty i elementárních částic, poznání elektromagnetismu odstartovalo průmyslovou revoluci … avšak o podstatě a vlastnostech času nevíme téměř nic!
Čas je příliš abstraktní – nehmatatelný, neviditelný – je bez chuti a bez zápachu. Všichni objektivně měříme čas hodinami a kalendáři, zároveň subjektivně vnímáme, že čas „letí jako splašený“ nebo mluvíme o „řece času“, která plyne svým neúprosným tempem a spravedlivě odměřuje čas každému z nás.
Z fyzikálního pohledu však o čase víme pramálo. Bez ohledu na to, jakého vzdělání se vám dostalo – v 99 % případů se s vámi nikdo nikdy nezamýšlel nad otázkou: Jakým způsobem, jakou rychlostí a jakým směrem se šíří čas naším světem, všudypřítomným prostorem, okolním vesmírem?
Až dnes!
Zamysleme se společně nad několika možnými scénáři, ve kterých se zároveň pokusíme přenést poznatky z našeho reálného světa i na onu imaginární veličinu „čas“:
3.4.2.1 DOMÁCÍ ÚLOHA PRO ZÁKLADNÍ ŠKOLY
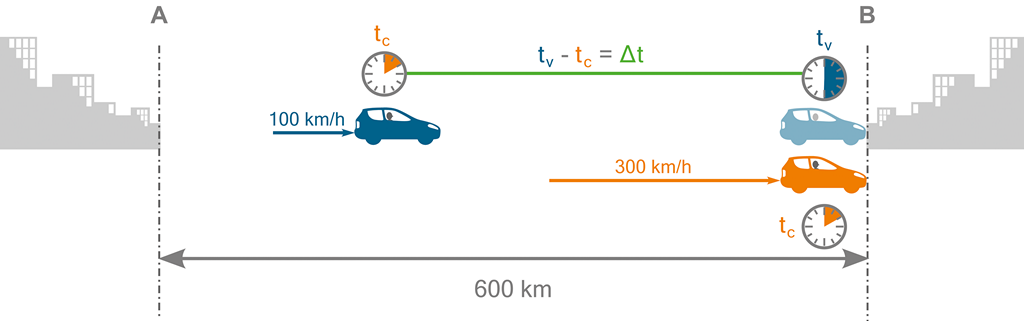
Z města A do města B, vzdálených od sebe 600 km, vyjedou současně dva automobily. První automobil pojede vysokou rychlostí c = 300 km/h, během času tc. Druhý automobil pojede běžnou rychlostí v = 100 km/h, během času tv. Časový rozdíl, o který dorazí první automobil do cíle dříve nežli automobil druhý, označme ∆t.
Určete:
1. Za jaký čas dojedou oba automobily do cíle (tc, tv)? Určete ∆t.
2. Definujte obecný vzorec (pro libovolné rychlosti) pro výpočet ∆t, pouze za použití proměnných v, c, tv.
Obrázek 88: Podobné úlohy řeší děti levou zadní!
Zkuste vyřešit nejprve sami a pak si zkontrolujte svá řešení. První úlohu vyřeší 99 % čtenářů, tu druhou zřejmě jen fandové matematiky (byť i ta je triviální):
Ad 1:
v = s / t
t = s / v
tc = 600/300 = 2 hod.
tv = 600/100 = 6 hod.
∆t = 6‒2 = 4 hod.
Ad 2:
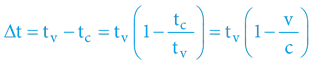
Čemu nás má tato jednoduchá úloha naučit?
Dostali jsme pro jakoukoliv podobnou situaci (obecný) matematický vzorec – fungující pro libovolné dva objekty pohybující se libovolnou rychlostí. Známe-li čas pohybu, během nějž se pohybuje pomalejší objekt (po dobu tv), je snadné spočítat rozdíl času oproti libovolnému rychlejšímu objektu pohybujícímu se po stejné dráze – stačí čas (tv) vynásobit koeficientem „k“:
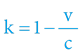
A jak nám má domácí úloha pro základní školy pomoci pochopit pojem času?
Chce to jen trochu představivosti a fantazie:
3.4.2.2 CO KDYŽ ZA VŠECHNO MŮŽE ČAS?
Ačkoliv si to běžně neuvědomujeme, po celou lidskou existenci – jsme poslední tisíce let v běžném životě i při vědeckých experimentech vycházeli z (mylného) předpokladu – že čas je v jakémkoliv místě prostoru (všude) identický – což bylo i Newtonovo chápání času a prostoru. A ačkoliv naše pocity, slovní výrazy a myšlenky často naznačují, že „čas letí“ či „nevstoupíš dvakrát do stejné řeky“, nikdy jsme tyto pocity nebrali vážně a v reálném světě s nimi naše logika nepočítá:
Trenér sprintera trénujícího na olympiádu stojí v poklidu na startu se stopkami v ruce a cílový čas svého svěřence „odmáčkne“ spolehlivě i ze svého stanoviště „v okamžiku“, kdy jeho svěřenec proběhne cílem. Ani na chvíli jej nenapadne, že je třeba běžet souběžně vedle sprintera či samotnému běžci vtisknout stopky do dlaně. Historie nás naučila, že nic takového není nutné – že „samozřejmě“ ve všech těchto případech stopky ukáží stejný čas.
S myšlenkou, že „Čas možná také běží nějakým směrem“, jsme v podobných situacích nikdy neuvažovali. Nezaznamenali jsme, že by bylo možné času nadběhnout, ani že by bylo možné času utéci – ať již běžíme kamkoliv.
Opravdu nelze času utéct?
Jakmile jsme přijmuli fakt, že zvuk se šíří omezenou rychlostí, pochopili jsme, že některé typy sportovních závodů již nelze objektivně startovat výstřelem z pistole – je nemožné zařídit, aby více závodníků zaslechlo výstřel „současně“!
Lidský intelekt samozřejmě našel řešení a jde-li o přesnost, není problém do stejné vzdálenosti za záda závodníků umístit příslušný počet reproduktorů a odstartovat závod současně zvukovým signálem vysílaným po kabelu z centrálního generátoru zvuku. Technický hnidopich by navíc dokázal v rámci objektivity zařídit i to, aby kabely byly ve všech případech stejně dlouhé – znaje skutečnost, že i elektrický signál se nešíří po vodiči nekonečnou rychlostí, ale rychlostí omezenou, byť velmi vysokou (téměř rychlostí světla).
Budou-li však závodníci v prostoru rozmístěni nepravidelně (třeba závod letadel, navíc na různých místech planety) – původně snadná úloha současného startu začne být hodně složitá. Budete-li mít velký rozpočet – možnost použití armádních GPS přijímačů, podaří se vám možná naprogramovat celý systém tak, aby všichni odstartovali současně (v rámci přesnosti GPS) – v konkrétní, předem dohodnutý, čas.
Lidský důvtip ani žádné technické řešení však neumí zajistit, aby závod začal na různých místech prostoru (planety) „současně“ s předem nenačasovanou událostí – například současně se stiskem tlačítka „START“.
Stiskne-li prezident USA v Oválné pracovně hypotetické červené tlačítko, v daný okamžik se nestane vůbec nic! Teprve až tuto událost rozdistribuují satelity a armádní servery do všech vojenských základen a „dohodnou“ si tak pokyn k „okamžitému a současnému“ útoku, bude moci začít „současný“ úder z jednotlivých míst planety. Pro planetu velikosti Země je nemožné zařídit, aby ona současná událost nastala za méně nežli jednu sekundu od stisknutí onoho červeného tlačítka. Stejně tak je nemožné, aby počítač na stole prezidenta obdržel potvrzení ze všech vojenských základen o zahájení útoku za méně nežli vteřiny dvě (od stisknutí tlačítka)!
Proč bude muset prezident USA čekat celé dvě vteřiny na potvrzení svého rozkazu, přestože nařídil „okamžitý“ útok?
Ano – jde o stejný „problém“, jaký nastává při komunikaci posádky Měsíční základny s pozemním střediskem NASA. Onu časovou prodlevu v komunikaci mezi dvěma místy v prostoru prostě nelze jakkoliv ošálit.
V běžném měřítku našich životů byl po tisíciletí lidské existence tento problém zanedbatelný. Při debatě dvou lidí z očí do očí příliš nevadí, že si musíte na odpověď toho druhého počkat o 0,00000001 sekundy déle. Stejně tak je tento problém zanedbatelný při tréningu sprintera.
Rozvoj vědy a techniky v posledním století nás však postupně nutí přehodnotit stereotypní uvažování a hledat nové odpovědi na naléhavé otázky ohledně času.
Problém faktického zpožďování komunikace mezi dvěma místy v prostoru může mít různá vysvětlení. Svést tento problém na omezenou rychlost šíření světla prostorem není řešením, neboť generuje další otázky:
Proč je rychlost šíření světla prostorem omezená?
Proč nemůžeme najít jinou formu hmoty (signálu), která se šíří rychleji nežli elektromagnetické vlnění?
Co způsobuje ono rychlostní omezení?
CO KDYŽ ZA VŠECHNO MŮŽE ČAS?
Jaké scénáře by v takovém případě přicházely v úvahu?
3.4.2.3 CO KDYŽ JE ČAS „UNIVERZÁLNÍ“ PRO CELÝ VESMÍR?
Tento scénář je de facto oním „starým“ předpokladem, s nímž v běžném životě dennodenně počítáme a který odpovídá chování trenéra při měření rychlostních výkonů svého svěřence. Jaký je takovýto předpoklad?
Mám-li já na hodinkách čas 00:00:00 (hh:mm:ss), má přesně tentýž čas jakékoliv místo v prostoru, kam až moje oko (či Hubbleův dalekohled) dohlédne – můj čas má „teď“ celý vesmír. Takto také přistupuji ke všem fyzikálním pozorováním. Vyšlu-li pozdrav posádce vesmírného modulu na Měsíci přesně ve 00:00:00, obdrží jej posádka v čase 00:00:01,25. A když mi oni odpovědí v čase 00:00:05, já obdržím jejich odpověď v čase 00:00:06,25.
Je to snadné – čas je všude stejný a já jen musím počítat s tím, že radiovému signálu trvá 1,25 vteřiny, nežli dorazí ze Země na Měsíc (či obráceně). Nevidím v ničem žádný problém. Čas je univerzální pro celé univerzum.
Ten nepříjemný „problém“ s prodlevami v komunikaci (omezená rychlost světla) se budeme snažit časem vyřešit. Například se pokusíme sestrojit komunikační technologie na bázi „tachyonů“ (hypotetické částice pohybující se vyšší rychlostí, nežli je rychlost světla). Vláda by měla investovat do výzkumu tachyonů pár miliard.
Modelový příklad:
Z planety A na planetu B, vzdálených od sebe 2 160 000 000 km, vyletí raketa v čase 00:00:00, rychlostí v = 100 000 km/s. Čas je univerzální v každém místě prostoru. Zakresleme takovou situaci a vypočtěme cílový čas:
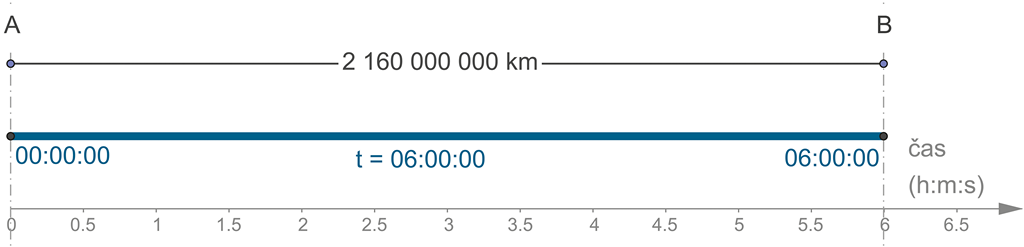
Obrázek 89: Čas je všude tentýž a úloha je proto triviální.
Výpočet je snadný:
Raketa dorazí do cíle za 6 hodin letu, v čase 06:00:00.
Abychom se vyhnuli problematice vlivu omezené rychlosti šíření světla, celý experiment sleduje pozorovatel z místa, které je umístěné na ose přesně uprostřed mezi oběma planetami. Pozorovatel sleduje tento děj de facto ze stejné perspektivy, jako čtenář nyní sleduje schematický obrázek.
Poznámka:
Kdybychom toto zjednodušení neprovedli (pozorovatel by zůstal na planetě A), experiment by vyšel identicky, pouze bychom museli provést matematické korekce (zohlednit, že další 2 hodiny bude trvat, nežli radiový signál o dosažení cíle dorazí zpět na planetu A).
Pozorovatel i kosmonaut v raketě zaznamenají úplně stejná měření:
Odstartovali jsme v čase 00:00:00 a přistáli jsme v čase 06:00:00. I v tomto vesmírném měřítku potvrdí experiment zkušenosti sportovního trenéra: Ať již čas měříme z pohybujícího se objektu, z místa startu, z místa cíle či z jakéhokoliv jiného místa – čas bude vždy identický! Čas je univerzální!
Tento předpoklad byl také jedním z hlavních východisek názorů Newtona – představa absolutního času. Newton hovořil o jednom jediném toku času, který zahrnuje celý svět a celý vesmír – představa o „současnosti“, která je totožná pro libovolně vzdálená místa v prostoru. Jde o stěžejní a naprosto zásadní princip klasické fyziky.
Dodejme jen, že v tomto scénáři zbývá odpovědět na otázku, proč jsme stále ještě (více jak 100 let po objevení podstaty hmoty, elementárních částic i elektromagnetického vlnění) neobjevili ony hypotetické částice (bájné tachyony), jež by se pohybovaly rychleji, nežli je ona omezující rychlost – „rychlost světla“.
Asi je třeba zvážit nějaký jiný scénář:
3.4.2.4 CO KDYŽ SE ČAS ŠÍŘÍ V NĚJAKÉM SMĚRU?
Co když se čas šíří naším prostorem rychlostí světla v nějakém konkrétním preferovaném směru? A co když shodným směrem poletí raketa?
Modelový příklad:
Z planety A na planetu B, vzdálených od sebe 2 160 000 000 km, vyletí raketa v čase 00:00:00, rychlostí v = 100 000 km/s. Čas se šíří stejným směrem rychlostí c = 300 000 km/s. Zakresleme takovou situaci a vypočtěme cílové časy:
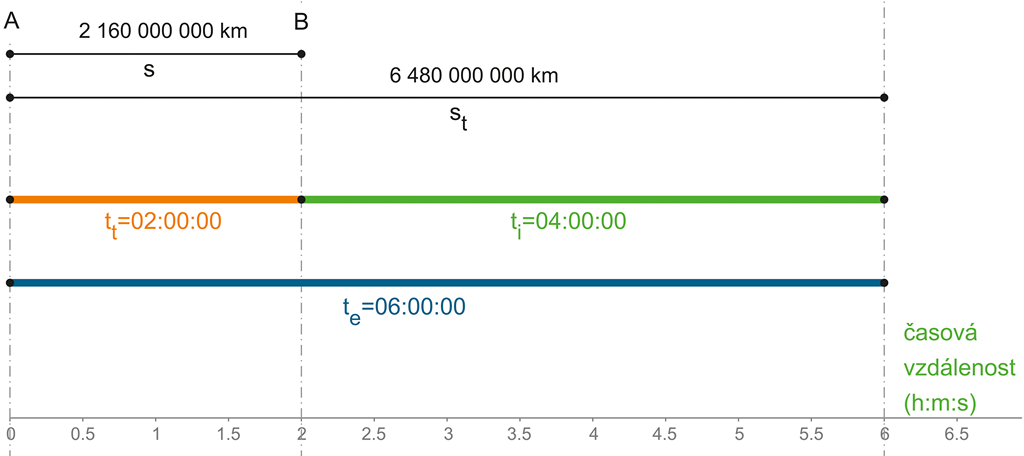
Obrázek 90: Ani tato úloha není složitá.
Výpočet je opět velmi snadný:
Raketa letí do svého cíle 3krát pomaleji nežli čas (čas během experimentu proto urazí 3násobnou vzdálenost). Čas dorazí do cíle již za 2 hodiny, zatímco raketě cesta do cíle trvá, z pohledu externího pozorovatele, 6 hodin.
Co zaznamená interní účastník experimentu (kosmonaut)?
Čas, který naměří interní účastník experimentu, je 4 hodiny – kosmonaut zaznamená čas kratší. Uspoří 2 hodiny, respektive naměří čas kratší – úměrně poměru své rychlosti a rychlosti času!
Vzpomeňme si na matematickou úlohu, kdy běžný a rychlý automobil cestovaly do společného cíle – z kapitoly Domácí úloha pro základní školy:
Principiálně jde totiž o analogickou situaci, jen s drobnou obměnou – namísto rychlého automobilu zde máme ČAS (prozíravě jsme již v předchozí úloze označili onu vyšší rychlost indexem „c“)!
Souputníkem rakety v tomto případě není závodní automobil, nýbrž samotný čas!
Z bodu A společně s raketou tedy startuje i časová koordináta, respektive se rychlostí „světla“ pohybuje časová osa. Startuje-li raketa v čase 0:00:00, pak samotnému času trvá 2 hodiny (tt), nežli čas „0:00:00“ dorazí do cíle. A přestože z pohledu fyziků na obou planetách bude let rakety trvat 6 hodin (te), kosmonauti v raketě budou mít v cíli na hodinkách čas 4:00:00 (ti).
Tak jako plavec plující SOUBĚŽNĚ po proudu řeky dorazí do cíle za kratší čas (nežli plavec volně splývající s proudem) – funguje v tomto hypotetickém případě proud řeky času.
Jakmile začínáme uvažovat o neuniverzálním čase, musíme začít časové údaje rozlišovat! Musíme se naučit odlišovat čas externího pozorovatele od času interního účastníka. Pro tento účel si opět připomeňme naši dohodu se čtenářem a zaveďme index „e“ a index „i“ jako obecnou syntaxi:
tečas děje měřený externím pozorovatelem děje
tičas děje měřený interním účastníkem děje
Obecný vzorec z naší domácí úlohy pro základní školy se v našem hypotetickém případě proto transformuje do podoby:

verychlost pohybujícího se objektu, z pohledu externího pozorovatele
cerychlost času, z pohledu externího pozorovatele (300 000 km/s)
Čas z pohledu interního účastníka je vůči času externího pozorovatele zkrácen koeficientem „k“:
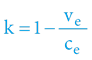
Jak ukazuje výšeuvedený vztah – matematický aparát světa, v němž by se čas pohyboval jedním směrem konkrétní rychlostí (kterou historicky nazýváme „rychlost světla“), by byl velmi jednoduchý. A protože se říká, že jeden obrázek vydá za 1000 slov – vyjádřeme si tuto situaci graficky. Koeficient „k“ je možno velmi snadno vyjádřit graficky následovně:
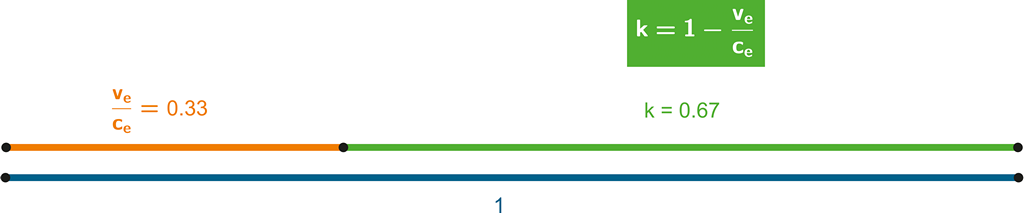
Obrázek 91: Koeficient je vyjádřen prostým odečtením dvou úseček.
Nicméně zůstává otázkou, nakolik je reálné, že žijeme v tak jednoduchém světě – ve kterém se čas šíří v našem 3D prostoru jedním konkrétním směrem. Najdeme spoustu pochybností, které naznačují, že spíše nikoliv:
Jaký směr je ten preferovaný? Jakým směrem se mám pohybovat prostorem, abych vyzrál nad časem a stárl pomaleji nežli moji statičtí vrstevníci? Který směr si čas vybral? Doleva? Doprava? Nahoru, či dolu? Směrem k souhvězdí Berana či spíše Vegy? Proč by měl vesmír nadržovat nějakému konkrétnímu směru? Takové představy vskutku nabízejí více otázek nežli odpovědí.
Pravděpodobně bychom v takovém světě při současném stavu technologií v kosmonautice a fyzice již narazili na onu nesymetričnost časoprostoru:
Vesmírné družice se pohybují prostorem řádově 10‒5 násobkem „c“, koeficient k by v takovém případě byl řádově 0,99999; přičemž atomové hodiny na palubě těchto družic dosahují mnohonásobně vyšší přesnosti a časové disproporce by musely být naměřeny spolu s tím, zda na své pouti tyto objekty letí ve směru, či protisměru onoho preferovaného toku času – v jednom případě by se hodiny na palubě družice zpožďovaly, ve druhém naopak. Nic takového praxe nepotvrzuje!
Zdá se tedy, že vztah prostoru a času bude o něco komplikovanější.
Jakému řešení se na počátku 20. století (mnohdy tak nějak mimoděk) přiblížili největší fyzici své doby? Co nám stihnul a co nestihnul předat Hermann Minkowski?
3.4.2.5 ČAS JAKO 4. ROZMĚR 4D ČASOPROSTORU
„Pohled na prostor a čas jako osamocené veličiny je napříště odsouzen ke zmizení do pouhé říše stínů. Pouze určitým spojením obojího bude možné vysvětlit náš reálný svět.“
Herman Minkowski
Fundamentálním principem představ Hermanna Minkowského a taktéž primárním východiskem TČ je tvrzení, že čas je reálně existujícím čtvrtým prostorem našeho světa a celého vesmíru. To, co nás obklopuje, není 3D prostor, nýbrž 4D prostor – časoprostor (prostoročas)!
Žijeme ve světě, který tvoří 4 na sebe navzájem kolmé roviny – 3 prostorové a 1 časová, přičemž ve třech prostorových rovinách se lze pohybovat libovolným směrem a čas „plyne“ ve čtvrté rovině jednosměrně „rychlostí“, která se historicky označuje jako „rychlost světla“, respektive – čas definuje kauzalitu a pořadí událostí!
Čas je dalším a přitom velmi specifickým rozměrem našeho prostoru – určuje pořadí a kauzalitu dějů (dává smysl pojmům příčina a následek), což je dáno jeho „jednosměrnou“ povahou – zatímco v délkových osách 3D prostoru se lze pohybovat libovolně tam i zpět, časová osa časoprostoru dává reálný fyzikální smysl pouze pohybu vpřed!
Ve výsledku se výšeuvedené projevuje tím, že světlu (elektromagnetickému vlnění) měříme omezenou rychlost, které říkáme „rychlost světla“, značíme ji „c“ (cca 3·108 m/s).
Pozorovaná omezená rychlost světla má příčinu ve způsobu, jakým se prostorem šíří událost – jde o geometrickou provázanost 3D prostoru a času, respektive o „geometrii kauzálnosti“ – jde o způsob, jímž se prostorem šíří následek jakékoliv příčiny.
Omezená rychlost „světla“ není projevem omezenosti pozemských technologií (proč jsme ještě neobjevili něco rychlejšího?). Jev „omezené“ rychlosti šíření světla je projevem něčeho hlubšího – času jakožto 4. rozměru našeho 4D světa!
Samotná číselná hodnota onoho „omezení“ c = 3·108 m/s přitom nemá žádný hlubší fyzikální význam – je dána historicky tím, jak nevhodně jsme definovali etalon metru a sekundy. V další kapitole vysvětlíme, že jednotky délky a času lze zvolit mnohem smysluplněji tak, aby reflektovaly onu „siamskou“ provázanost délkových a časových vzdáleností v rámci společného prostoru (časoprostoru).
Každému, kdo se s takovou představou setkává poprvé, může připadat představa vzájemně provázaného času a prostoru poněkud „nehomogenní“. Může se zdát, že prostor (respektive metr) a čas (respektive sekunda) jsou natolik odlišné kategorie, že představa jejich syntetického spojení v jeden funkční celek (časoprostor) je jen těžko představitelná.
Nicméně – prostor a čas (metr a sekunda) mají skutečně k sobě o hodně blíže, nežli se může zdát!
Zatímco okolní 3D prostor vnímáme svým zrakem i ostatními smysly a lidský mozek je tudíž vytrénován pro 3D vizualizaci, běh času žádný z našich smyslů nevnímá – „cítíme“ jej jaksi mimoděk, a proto je 4D časoprostor pro naši mysl „nepředstavitelný“. Přesto je to právě 4D svět, v němž reálně existujeme.
Ať již si představíme jakýkoliv pohybový stav (jakéhokoliv objektu) v našem 3D světě (vypuštění kosmické rakety na oběžnou dráhu, pohyb elektronů uvnitř kruhového urychlovače v Cernu, skákání na trampolíně či jen nehybné setrvávání v klidu) – v každém místě setrvávání daného objektu „letí“ čas prostorem kolmo ke směru pohybu (klid je pohyb nulovou rychlostí).
Tato skutečnost se projevuje tím, že jakýkoliv děj ve vesmíru se jeví externímu pozorovateli omezen v rychlosti šíření prostorem. Následek jakékoliv příčiny se nám (externistům) jeví jako pohybující se prostorem rychlostí 300 000 km/s, v důsledku čehož vnímáme i světlo omezené v rychlosti šíření.
Fakticky jde však o to, že „časová osa“ 4. rozměru (kolmá ke všem ostatním 3 rozměrům) „zapisuje“ časoprostorové souřadnice každého objektu v našem světě, a navíc jednosměrně!
Značíme-li tedy rychlost „světla“ symbolem c, korektnější by bylo značení ce – vždy jde o rychlost měřenou externě!
Přestože je v tomto ohledu 4D časoprostor pro náš mozek nepředstavitelný, je matematicky snadno a exaktně uchopitelný, s jistým zjednodušením dokonce i graficky (více či méně dobře) znázornitelný. Vzpomeneme-li na principy kapitoly Jak Minkowski objevil časoprostor, ohledně matematických poměrů v 1D, 2D a 3D prostoru, snadno pochopíme analogii:
Matematický aparát pro přechod z 3D do 4D prostoru si opět vystačí „jen“ s Pythagorovou větou (matematika základních škol).
Pythagorova věta je základem Teorie času!
Pro hlubší pochopení souvislostí (a pro matematické nadšence) však doporučujeme osvěžit si i vztahy v „jednotkové kružnici“, respektive trigonometrické funkce (matematika středních škol):
Znovu nám poslouží naše známá úloha v novém kabátě:
Z planety A na planetu B, vzdálených od sebe 2 160 000 000 km, vyletí raketa v čase 00:00:00, rychlostí ve = 100 000 km/s. Čas se šíří kolmo na dráhu pohybu rychlostí ce = 300 000 km/s. Zakresleme takovou situaci a vypočtěme cílový čas:
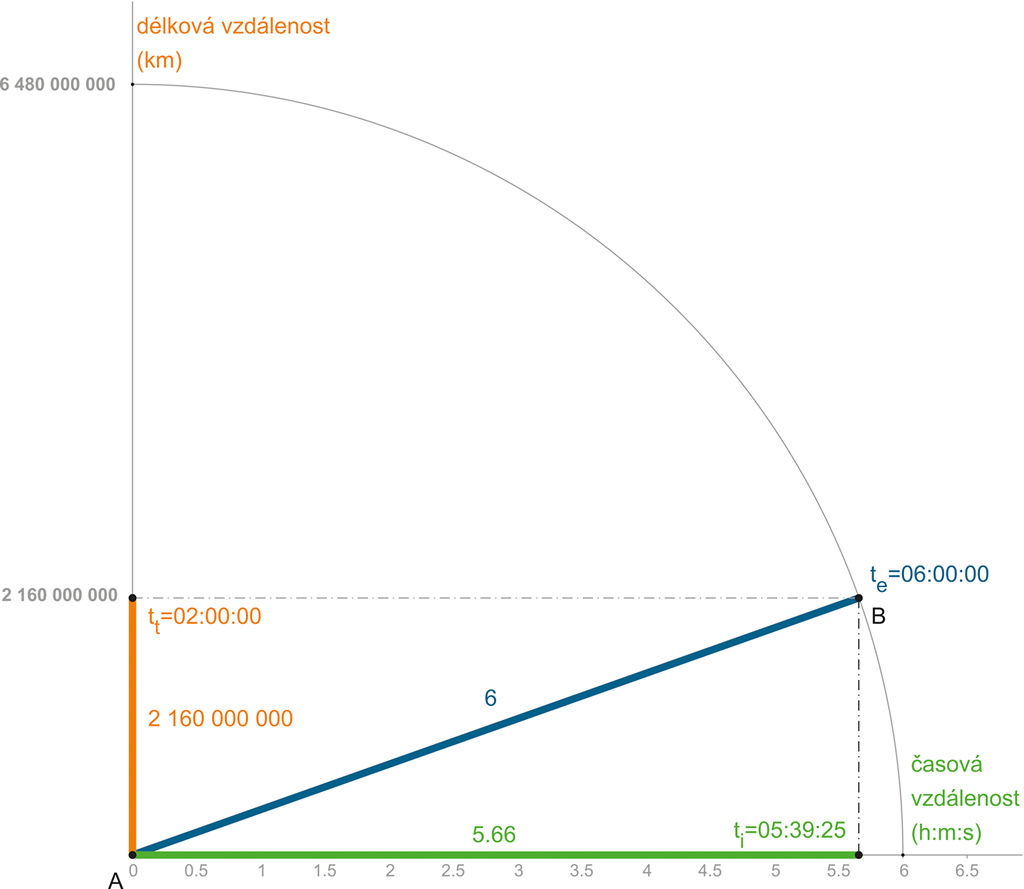
Obrázek 92: Úloha je snadno řešitelná – stačí Pythagorova věta.
Opět jde o (matematicky) snadnou úlohu:
Kosmická loď urazila (z pohledu externího pozorovatele) cílovou vzdálenost za te = 6 hodin, zatímco čas (pohybující se kolmým směrem 3× rychleji) by stejnou vzdálenost urazil již za 2 hodiny tt = 2 hodiny. V časoprostorovém trojúhelníku proto řešíme výpočet:
 ≈ 5,66 hodiny ≈ cílový čas 05:39:25
≈ 5,66 hodiny ≈ cílový čas 05:39:25
Tak jako plavec plující KOLMO vůči proudu řeky urazí za stejný čas větší vzdálenost (neboť se ve skutečnosti pohybuje diagonálně) – funguje v tomto hypotetickém případě kolmý proud řeky času.
Opět vyjádřeme obecný vztah pro transformaci časů:
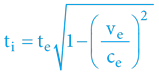
tičas děje měřený interním účastníkem děje
tečas děje měřený externím pozorovatelem děje
verychlost pohybujícího se objektu, z pohledu externího pozorovatele
cerychlost času, z pohledu externího pozorovatele (300 000 km/s)
Čas z pohledu interního účastníka je vůči času externího pozorovatele zkrácen (kontrakce času) koeficientem „k“:
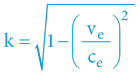
Pohotový čtenář v tomto okamžiku již možná zpozorněl – výšeuvedené vztahy jsou totožné s matematickým aparátem popisujícím dilataci času dle Einsteinovy TR!
K jejich odvození jsme potřebovali jeden jediný postulát: Čas je čtvrtým prostorem našeho světa.
Scénář 4D prostoru sestává z méně dogmat a nabízí více odpovědí.
Experimenty potvrzená omezená (limitní) rychlost světla zde není pouhým konstatováním. TČ objasňuje, že konstantní rychlost světla je pouze externím projevem existence „časoprostoru“ – je následkem geometrie 4D časoprostoru:
Čas je spravedlivý a nestranný. Nepreferuje žádnou ze 3 rovin našeho (dosud známého) světa. Čas má svůj vlastní směr, svou vlastní rovinu v prostoru – která je však pevně a exaktně provázána s naším známým 3D prostorem – rovina času je kolmá ke všem třem (tradičním) rovinám prostoru.
Náš svět, celý vesmír a každý jeho děj probíhá v prostoru a čase – zároveň a neoddělitelně:
• To, co je oddělené v prostoru, je oddělené i v čase a naopak!
• Dva oddělené body v prostoru jsou zároveň oddělené i v čase.
• Změnit své místo v prostoru zároveň znamená i přemístit se v čase.
• Dokonce i nehybný „klid“ ve skutečnosti znamená neustálé přemisťování se – a to v čase!
Pojem „současnost“ ve svém exaktním kontextu je nesmyslnou kategorií, respektive pouhou iluzí. Oba pojmy „soumístnost“ i „současnost“ postrádají smysl – dva hmotné body v prostoročase nikdy nemohou sdílet shodnou pozici. Pozice (bodu či hmoty) v prostoru (časoprostoru) je vždy unikátní a jedinečná.
Prostor (ve smyslu délek) a čas jsou si bližší, nežli nás učili ve škole. Čas a prostor jsou dvě tváře téhož – společně tvoří časoprostor.
Nakolik může znít toto slovní spojení nehomogenně či jako „slepenina“, jde o konzistentní entitu – tvořící náš svět. Částečný zmatek v chápání 4D prostoru nám sice opět dělá čeština, respektive pojmy „časoprostor“ a „prostoročas“ (pojem „prostor“ má v sémantickém i fyzikálním smyslu nejen délkový, ale i časový charakter) – tyto námitky však nemohou nic změnit na skutečnosti, že reálně všichni existujeme ve 4D časoprostoru, kde všechny živé i neživé objekty se neustále pohybují v prostoru i čase, přičemž tyto dvě zdánlivě rozdílné kategorie jsou ve skutečnosti geometricky zcela exaktně provázané a závislé.
Panta rei!
Herakleitova slova o tom, že „vše plyne – veškeré jsoucno je v neustálém pohybu“ dostávají v souvislosti s časoprostorem nádech věštby. Uplynula tisíciletí a novodobá věda dává starověkému moudru Řeků za pravdu:
Klid neexistuje. Všichni a všechno jsou součástí neustálého pohybu, a to nikoliv pouze onoho pohybu zjevného (délkového). Veškerý vesmír a hmota v něm „plynou“ řekou času, respektive čas protéká každým bodem našeho zjevného 3D světa oním čtvrtým, neviditelným (kolmým) směrem.
Prostor a čas již nemohou být další staletí vnímány a zkoumány odděleně. Metr a sekunda jsou blíženci!
Pro čtenáře, který se s „logikou“ časoprostoru setkává prvně, mohou být taková tvrzení zprvu příliš radikální a příliš nová. Není snadné přemluvit mozek ke snaze o chápání 4D světa – k vnímání onoho jednoduchého geometrického vztahu mezi metrem a sekundou. Zpočátku může být nesnadné spatřit onu geniální jednoduchost pravoúhlého trojúhelníka, je-li jedna jeho strana délkou a druhá trváním.
Buďte však bez obav – v následující kapitole to všem usnadníme:

