3.4.7 RESUMÉ PRO LIMITNÍ POHYBOVÉ STAVY
Z matematiky pravoúhlého trojúhelníku (respektive trigonometrických funkcí) plynou i vysvětlení, proč a jak interpretovat svět velmi pomalých a velmi vysokých rychlostí. Jde o závěry samozřejmé pro matematické nadšence a zajímavé pro příznivce matematiky, kterým je blízký matematický formalismus „limit funkcí“ (limita funkce je základním nástrojem matematické analýzy).
Všichni ostatní ať raději následující podkapitoly přeskočí a pokračují kapitolou Cestování ke hvězdám!
3.4.7.1 SVĚT NÍZKÝCH RYCHLOSTÍ
Při běžných (lidstvem dosažitelných) rychlostech pohybu se časoprostorový úhel α blíží nule α→0, a proto náš svět nevykazuje de facto žádné časové či rychlostní disproporce a jiné „podivnosti“. Důvodem je triviální matematika pravoúhlého trojúhelníku (jednotkové kružnice) pro velmi malé úhly:
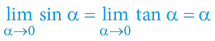
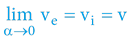
Výšeuvedené vysvětluje, proč při běžných lidstvem dosažitelných rychlostech pohybu (α→0) nepozorujeme žádné disproporce v naměřených rychlostech.
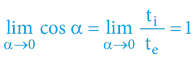
Výšeuvedené vysvětluje, proč při běžných lidstvem dosažitelných rychlostech pohybu (α→0) nepozorujeme žádné disproporce v naměřených časech (trvání dějů).
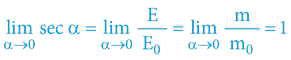
Výšeuvedené vysvětluje, proč při běžných lidstvem dosažitelných rychlostech pohybu (α→0) nepozorujeme žádnou změnu hmoty tělesa (respektive změnu celkové energie tělesa) – lopata uhlí v jedoucí či stojící lokomotivě je vždy stejně těžká a dodává vždy stejné množství tepla (páry).
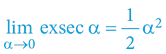
Výšeuvedené vysvětluje, proč při běžných lidstvem dosažitelných rychlostech pohybu (α→0) je kinetická energie pohybujícího se tělesa přímo úměrná druhé mocnině jeho rychlosti (poznatek Leibnize), respektive že pro těleso o jednotkové primární energii platí přibližný vztah:
Ek = ½ v2
Pro předmět o libovolné hmotnosti pak platí (při „běžných“ rychlostech) známá podoba vzorce:
Ek = ½ E0 v2 = ½ m0 v2
3.4.7.2 SVĚT MAXIMÁLNÍCH RYCHLOSTÍ
Při rychlostech pohybu blížících se maximu – elektromagnetické záření (světlo) a částicová fyzika – se prostorový úhel α blíží 90° (respektive π/2) α→π/2, a proto můžeme experimentálně pozorovat velmi zásadní „podivnosti“. Důvodem je opět matematika pravoúhlého trojúhelníku (jednotkové kružnice):
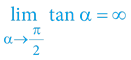 ; respektive
; respektive  ;
;
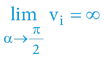 ; respektive
; respektive  ;
;
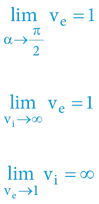
Výšeuvedené vysvětluje, proč objekt pohybující se prostorem nekonečnou rychlostí (z pohledu svého interního běhu času) se externím pozorovatelům jeví jako objekt pohybující se omezenou „jednotkovou“ rychlostí – rychlostí času (světla).
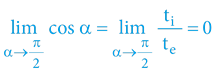
Výšeuvedené vysvětluje, proč čas (trvání interních dějů) pohybujícího se objektu prostorem maximálním prostorovým úhlem (maximální rychlostí) se jeví z pohledu externího pozorovatele jako „zamrznutý“ v čase, respektive nulový.
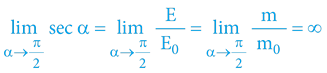
Výšeuvedené vysvětluje, proč žádný hmotný objekt (s nenulovou primární hmotností) nemůže dosáhnout maximální rychlosti – maximálního prostorového úhlu (rychlosti času, respektive „světla“ z pohledu externího pozorovatele). K dosažení takovéhoto pohybového stavu by bylo zapotřebí nekonečné množství energie, respektive nekonečné množství „paliva“ k urychlení objektu.

