3.6.13 GRAVITAČNÍ POTENCIÁL
Z předchozích kapitol plyne, že gravitační potenciál (V) je stěžejním atributem gravitace a přímo definuje míru pohybu pro „látkové“ objekty a přírůstek či úbytek energie (frekvence) elektromagnetického záření (fotonů). TČ finálně modifikovala vztah pro gravitační potenciál takto:
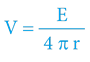 ; bezrozměrná veličina (jednotka: 1)
; bezrozměrná veličina (jednotka: 1)
Co si však máme pod pojmem gravitační potenciál představit? A proč má výšeuvedený vzorec právě takovou podobu?
Odpověď souvisí s matematikou koule, respektive povrchem koule:
Plocha koule S = 4πr2
Již v minulé kapitole jsme zmínili, že povrch „jednotkové koule“ (koule o poloměru r = 1 m) má plochu téměř 13 m2 (4π). Koule o poloměru 10 metrů má plochu 100krát větší (nikoliv 10krát) – plocha koule totiž roste s kvadrátem (druhou mocninou) poloměru!
V reálném světě narážíme na stejný fenomén u všech radiálních „polí“ – jejich intenzita vždy klesá s kvadrátem vzdálenosti stejně tak, jako s onou vzdáleností roste plocha pomyslné „kuloplochy“. Tato závislost platí pro elektrická i magnetická pole, pro elektromagnetické záření (světlo), a dokonce i pro šíření zvuku. Obecně lze říci, že intenzita energie jakéhokoliv centrálního (či bodového) zdroje klesá při svém šíření prostorem dle výšeuvedeného vzorce – důvodem je (se vzdáleností) rostoucí povrch kuloplochy.
Intenzita 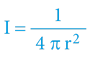
Totéž samozřejmě platí i pro gravitaci a nic na tom nemění skutečnost, že vůbec netušíme mechanismus gravitační interakce: Jaké částice gravitaci zprostředkovávají? Kde se ty záhadné částice v „prázdném“ vakuu berou?
Každý hmotný objekt tak sestává nejen z prostorově ohraničené látky, ale i prostorově neohraničeného gravitačního pole – jehož intenzita klesá se vzdáleností stejně tak, jako roste plocha pomyslné koule a v této rostoucí ploše se „ředí“ intenzita gravitace.
Opět můžeme použít analogii s žárovkou – sebedokonalejším kolektorem o ploše 1 m2 ve vzdálenosti 1 metr od zdroje – dokážeme zachytit maximálně 1/13 emitovaného záření (a emitované energie).
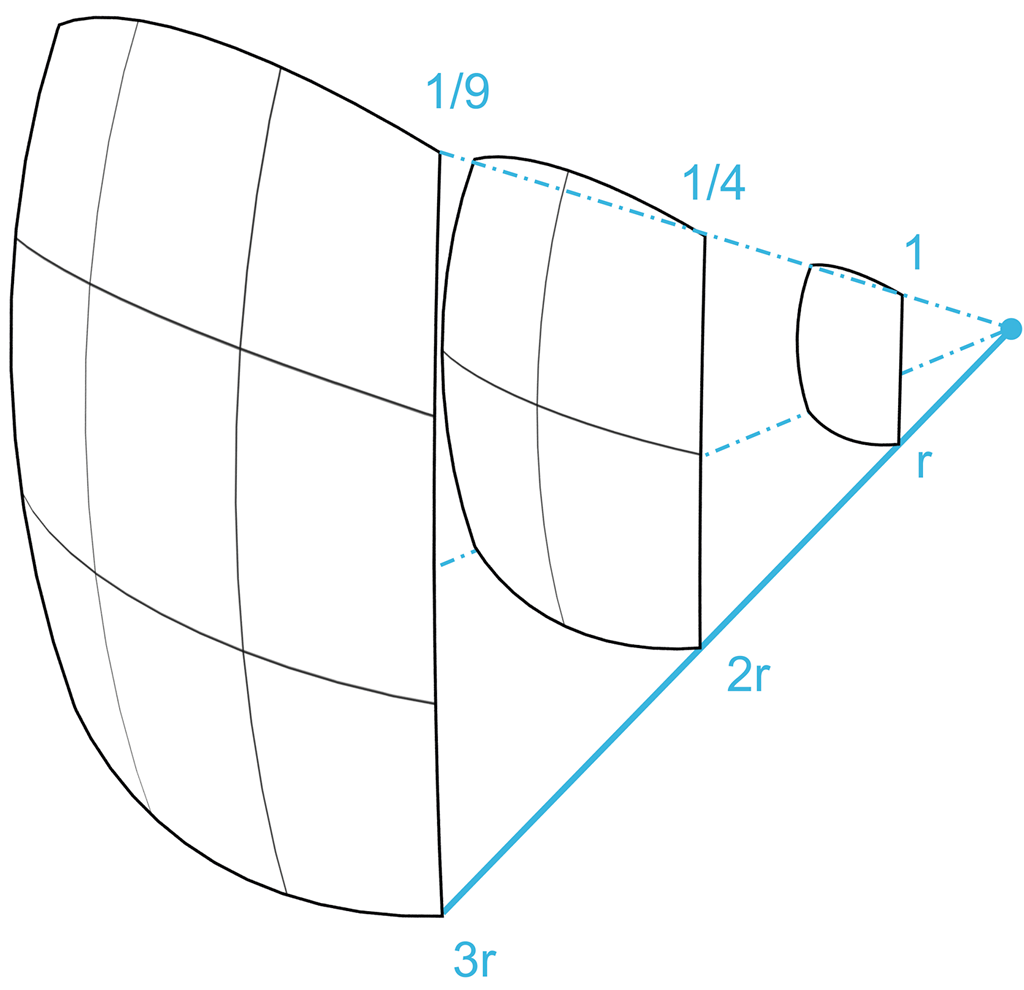
Obrázek 144:
Intenzita klesá s druhou mocninou vzdálenosti.
Proč je však ve vzorci pro gravitační potenciál pouze prvá mocnina vzdálenosti (nikoliv druhá)?
Intenzita gravitačního pole má sice ke gravitačnímu potenciálu velmi blízko, přesto nesmíme tyto dvě veličiny zaměňovat:
Intenzita je údajem „okamžitým“, zatímco potenciál je údajem „průběžným“! Intenzita nám říká, jak silné je gravitační pole v určité konkrétní vzdálenosti, potenciál nám říká, kolik „gravitace“ se mezi dvěma body v součtu nalézá.
Potenciál de facto vyjadřuje celkový „součet intenzit“ mezi dvěma vzdálenostmi (z nichž jedna je zpravidla nekonečno). Pozorný čtenář již asi tuší, že „sčítání“ čehokoliv vede i tentokrát k integrálnímu počtu:
Ano!
Gravitační potenciál je integrálem intenzity gravitace (integrace dle vzdálenosti). Hodnota gravitačního potenciálu tak přímo odpovídá na otázku, kolik energie získá těleso padající z nekonečna (kde je intenzita gravitace limitně nulová) během své cesty do konkrétního místa ve vzdálenosti „r“ od zdroje gravitace.
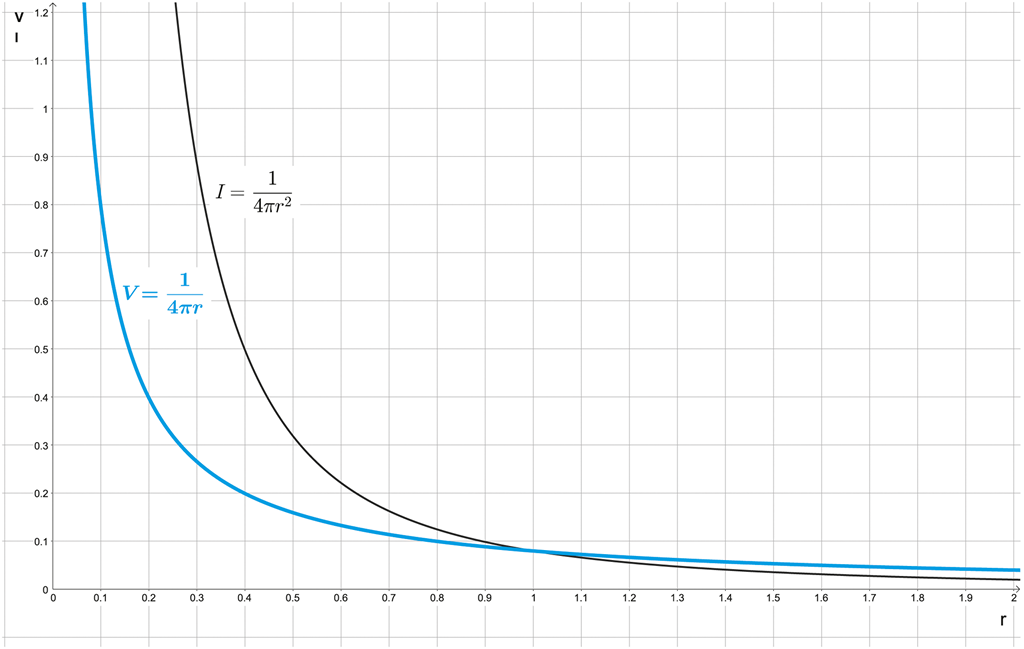
Obrázek 145:
Gravitační potenciál je integrálem intenzity.
A protože integrování funkce 1/x2 vede k funkci 1/x, je výsledný matematický vztah pro výpočet gravitačního potenciálu „jen“ s prvou mocninou vzdálenosti:
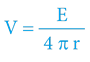
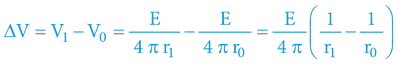
Kde V1 > V0, respektive r0 > r1 tak, aby rozdíl ∆V byl kladný.
Resumé:
Pro názornější pochopení gravitace je dobré vědět, že základem rovnice pro výpočet gravitačního potenciálu je vzorec pro výpočet plochy koule.
Hodnota gravitačního potenciálu na povrchu Slunce (E = 6,19·10‒5 sg; r = 2,32 s) je 2,12·10‒6. Ve vhodně zvolené soustavě jednotek TČ jde o veličinu, která říká, že jakékoliv těleso získá během svého pádu k povrchu Slunce navíc 0,00000212násobek své původní energie (ve formě energie kinetické). Kilogramový etalon tak bude v okamžiku dopadu na Slunce ekvivalentem 1,00000212 kg – bude zde hmota i energie navíc! Dvoukilogramové závaží bude při dopadu ekvivalentem 2,00000424 kg.
Bez ohledu na hmotnost těles – dopadová rychlost „volného pádu“ z nekonečné (či hodně veliké) vzdálenosti je na povrchu Slunce vždy cca 0,002 (618 000 m/s). Rozdíl v měření externí a interní rychlosti bude „jen“ 1 m/s, protože kontrakce času bude „pouhých“ 0,999998.
A co kdyby se Slunce 10× zmenšilo (rozměrově), kdyby se zhroutilo vlastní tíhou a jeho poloměr by klesl na pouhou desetinu? Mělo by to nějaký vliv na výsledek experimentu?
Energie (hmota) Slunce by zůstala nezměněna, a proto by ve vzdálenosti 2,32 s (původní poloměr) byl stále stejný gravitační potenciál. V daném místě trajektorie volného pádu by tudíž mělo každé těleso opět 1,00000212krát větší energii nežli na startu a opět stejnou rychlost 0,002 (618 km/s).
Rozdíl bude jen v tom, že (v daném hypotetickém scénáři) těleso v této části své cesty ještě nenarazí na povrch Slunce, ale jeho „pád“ bude moci pokračovat – s každým dalším metrem bude těleso indukovat více energie (intenzita gravitace roste s kvadrátem klesající vzdálenosti), ještě více tedy poroste přírůstek kinetické energie a s ním i rychlost.
Těleso by tak dopadlo na povrch Slunce rychlostí cca 0,0065 (1 953 km/s), s přírůstkem energie (hmotnosti) 2,12·10‒5.
V závěrečných kapitolách se k podobnému scénáři vrátíme podrobněji – v názorných příkladech.
Pro tuto chvíli bude stačit, když si zopakujeme veledůležitý význam gravitačního potenciálu:
Gravitační potenciál je souhrnná veličina přímo kvantifikující přírůstek energie vůči prvotní energii tělesa, jež se pohybuje mezi jednotlivými hladinami s rozdílnou intenzitou gravitačního pole.
Gravitační potenciál nezávisí na rozměrech (poloměru) objektu, tyto parametry pouze ovlivní, v jaké vzdálenosti (od centra gravitace) volný pád tělesa skončí a těleso vrátí svoji kinetickou energii okolní (látkové) hmotě!

