3.6.15 GRAVITAČNÍ PROBLÉM 2 TĚLES VE 4D ČASOPROSTORU
K vysvětlení okolního světa není třeba ohýbat prostor ani generovat Temnou hmotu. Stačí jediné – Newtonovy gravitační zákony řešit ve 4D časoprostoru a nezapomenout na symetrii pohybu. Newton považoval čas za „univerzální“ a to byl jeden z jeho mylných předpokladů – v časech Newtona však neexistoval jediný experiment, který by nutil Newtona své předpoklady přehodnotit.
Dle jednoduchých principů a jednoduché matematiky TČ – stačí pouze obohatit Newtonovu gravitaci o symetrický pohyb objektů ve 4D euklidovském časoprostoru (ideálně v rámci racionalizovaných jednotek).
Vyřešme tedy (Newtonovu) úlohu 2 těles ve 4D časoprostoru, kde čas je čtvrtým rozměrem (kolmým ke třem délkovým rozměrům) a kde se hmota pohybuje symetricky vůči svému barycentru v důsledku kinetické energie indukované gravitačním potenciálem:
Již v kapitole 3.4.6 jsme si objasnili, že přírůstek kinetické energie je v časoprostorové kružnici vyjadřován funkcí exsecans, jež je (v rámci racionalizace jednotek TČ) přímo definována gravitačním potenciálem. Celkový gravitační potenciál obou těles tudíž musí být mezi tělesa rozdělen takovým způsobem, aby byla zajištěna symetrie pohybu.
Musí tedy platit:
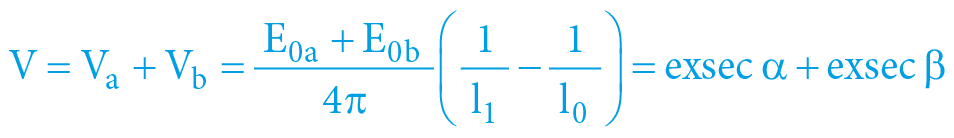
Přičemž energetická (hmotnostní) symetrie pohybu a pythagorovská matematika jednotkové kružnice časoprostoru vyžadují, aby:
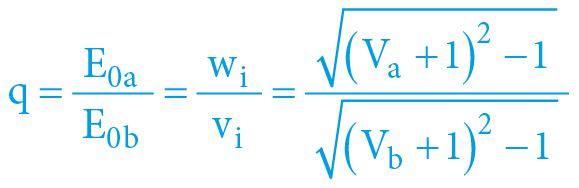
Soustava výšeuvedených rovnic má analytické řešení a lze tedy dojít k výpočtu gravitačních potenciálů jednotlivých objektů, z kterého plyne, že:
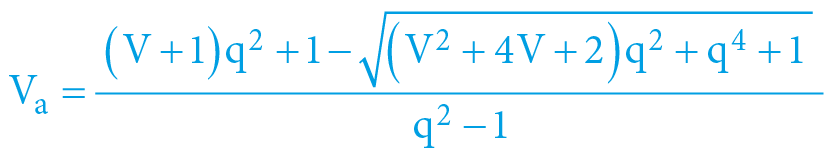
Vb = V – Va
Dopočítat všechny zbývající veličiny je následně (na základě výchozích rovnic) již triviální – dilataci i (reciproční) kontrakci časů, obě rychlosti interní, obě rychlosti externí i „sečtené“ vzájemné rychlosti (tělesa vůči sobě navzájem) – spočteme již snadno na základě zjištěných časoprostorových úhlů – dle matematiky předchozích kapitol:
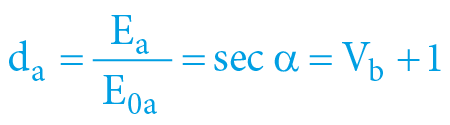
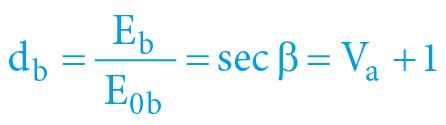
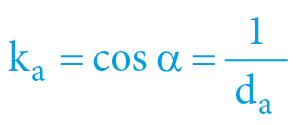
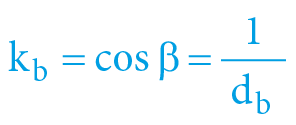
α = arcexsec Vb = arcsec da = arccos ka
β = arcexsec Va = arcsec db = arccos kb
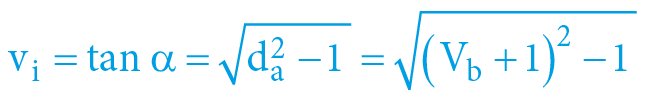
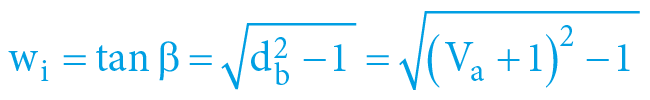
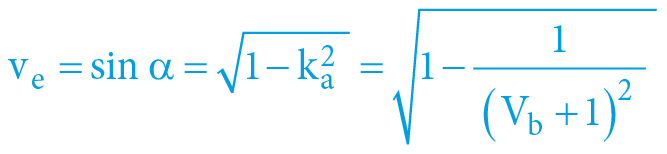
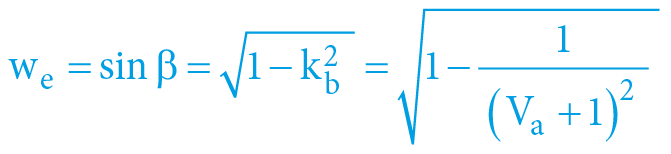
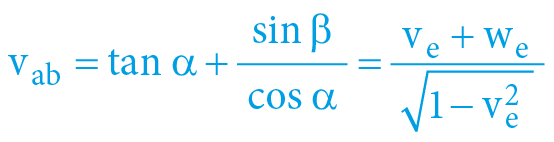
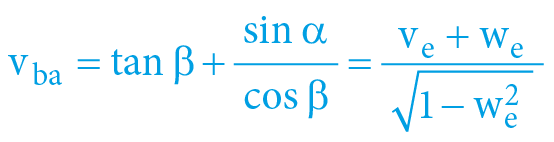
Přičemž:
Vsouhrnný gravitační potenciál obou objektů [1]
Vagravitačního potenciál „budícího“ hmotného objektu A (indukuje objektu B pohyb) [1]
Vbgravitačního potenciál „budícího“ hmotného objektu B (indukuje objektu a pohyb) [1]
E0aprimární energie hmotného objektu A [sg]
E0bprimární energie hmotného objektu B [sg]
q hmotnostní poměr mezi oběma objekty q = E0a/E0b
l0počáteční vzdálenost obou objektů [s]
l1konečná vzdálenost obou objektů [s]
αindukovaný časoprostorový úhel pohybu prvého objektu (vůči barycentru) [rad]
βindukovaný časoprostorový úhel pohybu druhého objektu (vůči barycentru) [rad]
3.5.15.1. LIMITNÍ ZJEDNODUŠENÍ:
Pakliže hmotnost jednoho objektu mnohonásobně (řádově) převládá (např. E0a >>E0a), pak se hmotnostní poměr (q) limitně blíží nule (tedy i Va→0) a celkový gravitační potenciál je definován pouze hmotností dominantního tělesa (V = Vb). V takovémto případě můžeme „zanedbat“ i symetrii pohybu – hmotnostně dominantní těleso můžeme považovat za nehybné (neb samo je de facto barycentrem) a veškerého pohybu se účastní pouze „zanedbatelně hmotné“ těleso. Takovou situaci známe například z nebeské mechaniky a problematiky „kosmických rychlostí“.
V takovém případě se vše zjednoduší na (již známé) vztahy:
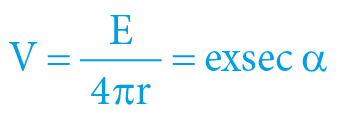
d = sec α = V + 1
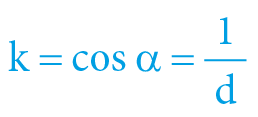
α = arcexsec V = arcsec d = arccos k
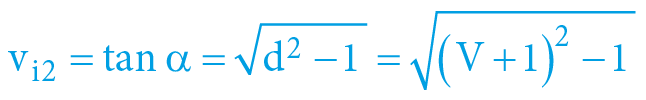
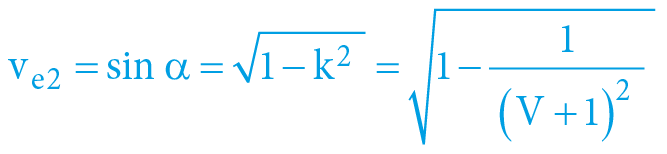
3.5.15.2. LIMITNÍ ZJEDNODUŠENÍ PRO „POMALÉ“ DĚJE:
Pakliže je (navíc k předchozí situaci) gravitační potenciál relativně malý (například v reáliích naší Sluneční soustavy), bude výsledný pohyb „pomalý“ (nesouměřitelný s rychlostí světla) a znovu se tak projeví skutečnost, že pro malé úhly lze časoprostorovou trigonometrii zanedbat, neb pro velmi malá čísla (přibližně) platí:
α ≅ sin α ≅ tan α
![]()
U takto „pomalých“ dějů lze tudíž matematický aparát ještě více zjednodušit – pak je čas pro všechny stejný (dilatace i kontrakce času jsou neměřitelné), i rychlost je analogicky pro všechny stejná a závislost druhé kosmické rychlosti na gravitačním potenciálu lze tedy přibližně popsat (tradičním) vztahem newtonovské gravitace (v rámci racionalizovaných jednotek TČ):
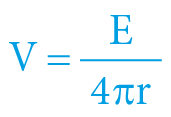
![]()
3.5.15.3. DVA HYPOTETICKÉ OBJEKTY
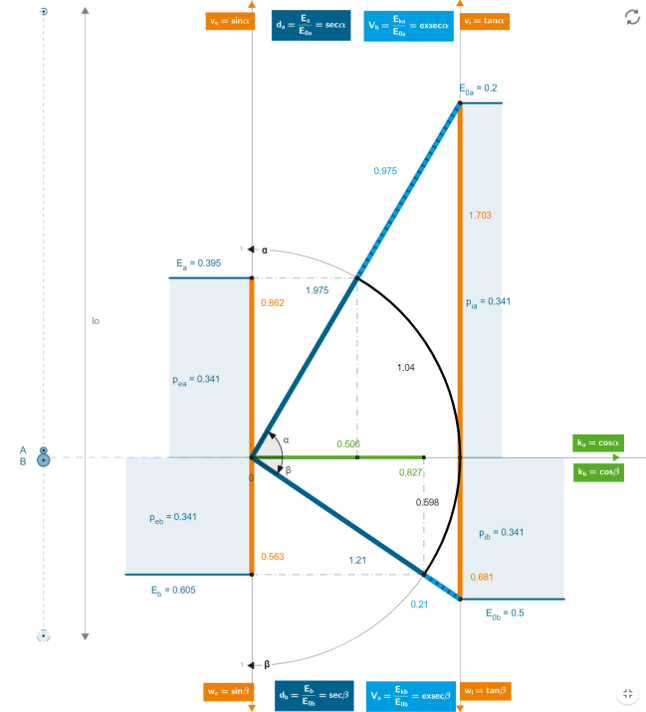
Máme dva hmotné objekty v prostoru o energii (hmotnosti) Ea a Eb; o poloměrech ra a rb; ve vzájemné vzdálenosti l0; které se začnou vlivem gravitace pohybovat směrem k sobě (respektive ke svému společnému barycentru):
E0a = 0,2 sg (6,4E+33 kg); E0b = 0,5 sg (1,6E+34 kg)
ra = 0,0163 s; rb = 0,03 s; l0 = 3 s
Jak bude vypadat dynamika obou objektů při srážce (v okamžiku, kdy se povrchy obou objektů střetnou)?
Následující obrázek graficky popisuje danou situaci, kdy celkový gravitační potenciál (obou těles) přímo určuje dynamiku obou objektů – ve smyslu výšeuvedených matematických vzorců.
Celkový gravitační potenciál těles je společně „sdílen“ tak, aby byla zajištěna symetrie pohybu (Zákon zachování hybnosti), v rámci 4D euklidovského časoprostoru:
Obrázek 145:
ANIMACE
Situace při srážce
(srovnej s obr. 121)
3.5.15.4. VÝPOČET PRO VZOROVÝ PŘÍKLAD
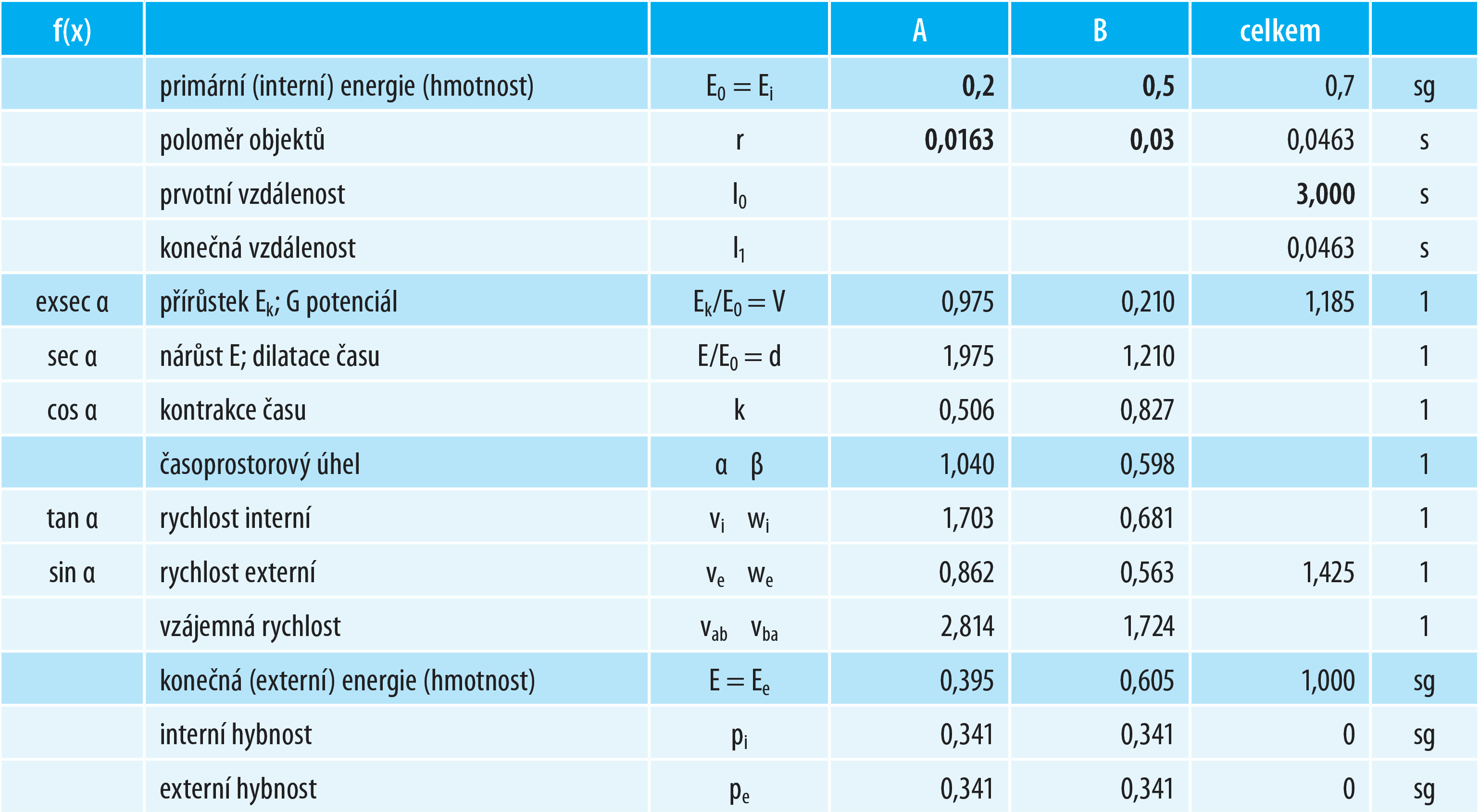
Tabulka 8: Zadání a výsledky
Oba objekty se budou pohybovat poměrně vysokými rychlostmi (neboť oba produkují velmi silný a srovnatelný gravitační potenciál):
V okamžiku srážky bude rychlost objektu A z pohledu externího barycentra rovna 0,862 (2,6·108 m/s), obrácenou perspektivou interního pozorovatele se bude objekt A přibližovat k barycentru rychlostí 1,703 (5,1·108 m/s) – onen rozdíl bude mít příčinu v časových disproporcích (d = 1,975).
V okamžiku srážky bude rychlost objektu B z pohledu externího barycentra 0,563 (1,7·108 m/s), obrácenou perspektivou interního pozorovatele se bude objekt B přibližovat k barycentru rychlostí 0,681 (2·108 m/s) – onen rychlostní rozdíl bude mít příčinu v časových disproporcích (d = 1,21).
Vzájemná rychlost z pozice objektu A vůči objektu B bude 2,814 (8,4·108 m/s). Z opačné perspektivy (B vůči A) bude rychlost rovna 1,724 (5,2·108 m/s).
Zároveň je nutné zdůraznit, že dnešní vesmír je již natolik „zředěný“, že výše popsaná modelová situace v něm de facto nemůže nastat – v blízkém vesmíru nenajdeme natolik hmotné objekty dostatečně blízko sobě. Vesmírné makro-objekty se tudíž nepohybují rychlostmi srovnatelnými s rychlostí „světla“ – v reálném vesmíru proto nedochází k zásadním časovým disproporcím při pohybu nebeských makro-těles!
3.5.15.5. SLUNCE A METEOR
Představme si nehybný meteor (B) o hmotnosti (energii) 3,11·10‒32 sg (1000 kg) a poloměru 3,33·10‒9 s (1 m) na okraji naší SS, ve vzdálenosti jednoho světelného roku (1 LY ≈ 9,5·1015 m ≈ 3,17·107 s) od Slunce. Gravitace Slunce (A) jej začne zvolna přitahovat. Jak bude vypadat situace, když se oba nebeské objekty střetnou?
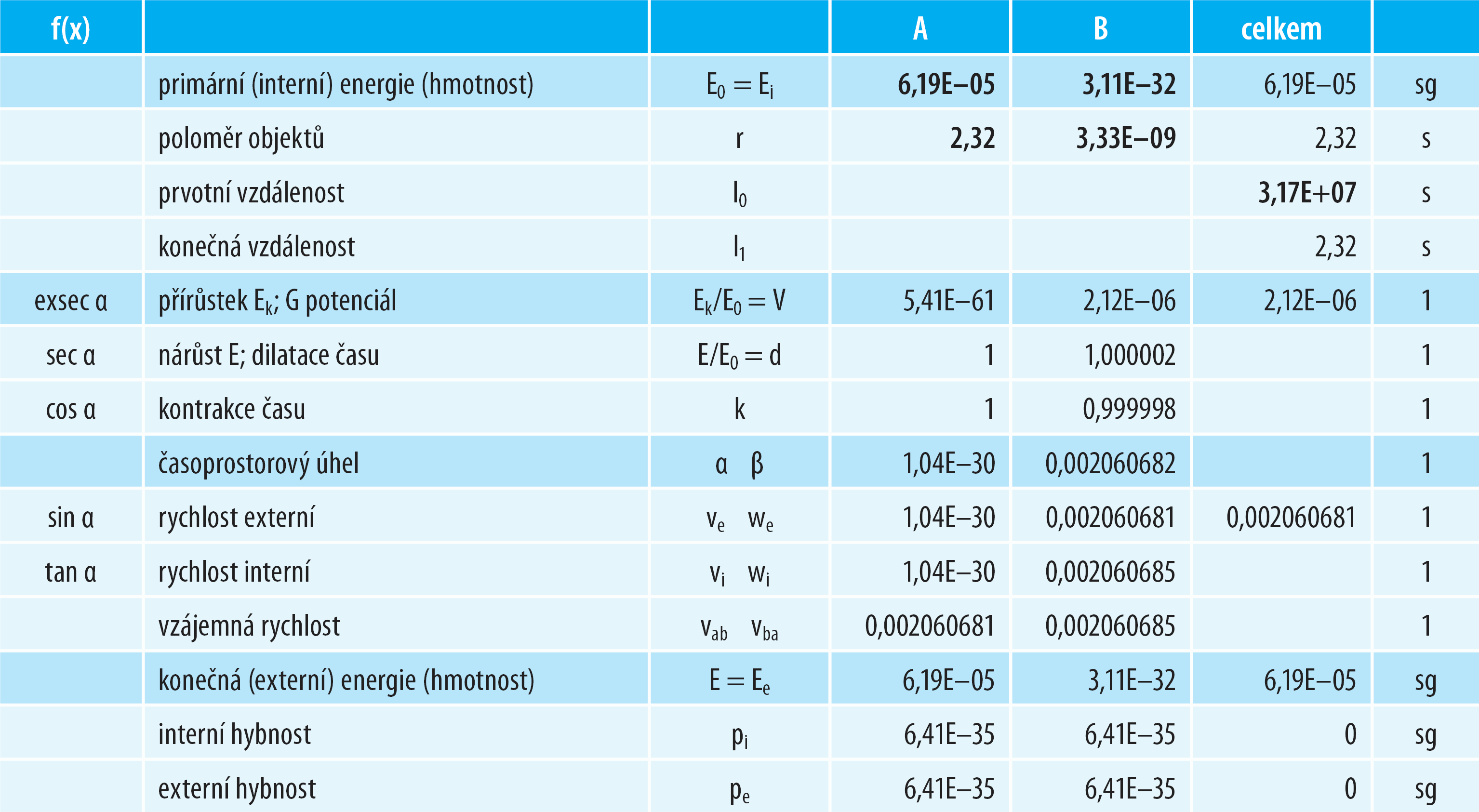
Tabulka 9: Zadání a výsledky
Hmotnostní poměr obou těles je tak obrovský ve prospěch Slunce, že se Slunce de facto nepohne z původního místa v prostoru – jeho rychlost před srážkou tedy bude fakticky nulová (1,04·10‒30 = 3·10‒22 m/s).
Meteor se však srazí se Sluncem rychlostí 0,002060681 (617 776,5 m/s), bude-li rychlost měřena z pohledu Slunce. Vlivem kontrakce času však bude srážková rychlost z pozice meteoru činit 0,002060685 (617 777,8 m/s). V našich „skromných“ poměrech Sluneční soustavy tak časové disproporce 4D prostoru zapříčiní rozdíl v rychlosti pouhých 4·10‒9 (1,3 m/s), neboť čas bude deformován jen velmi nepatrně (d = 1,000002)!
Všimněme si, že vypočítaná rychlost meteoru při dopadu na povrch Slunce (ať již ve či vi) je totožná s druhou kosmickou rychlostí uváděnou pro Slunce (viz Druhá kosmická rychlost), protože „pád“ ke Slunci z tak veliké vzdálenosti je de facto „obráceným“ mechanismem oproti vystřelení tělesa „až za hranice“ gravitace.
Rychlost pádu z „nekonečné vzdálenosti“ je totožná únikové rychlosti, respektive 2. kosmické rychlosti!
Právě proto, že uvedený scénář reprezentuje zcela zásadní hmotnostní dominanci jednoho (ze dvou) těles – lze v tomto případě zanedbat symetrii pohybů (pohyb Slunce) – „problém dvou těles“ můžeme degradovat na „problém jednoho tělesa“ a použít tudíž jednodušší matematiku (viz Limitní zjednodušení).
Dilatace času i obě rychlosti meteoru (interní versus externí) vyjdou i s touto (jednodušší) matematikou totožně.
Taktéž je třeba si uvědomit, že naše „gigantické“ Slunce produkuje jen relativně „slabý“ gravitační potenciál (například v kontextu neutronových hvězd), tělesa v jeho gravitačním poli se tudíž pohybují relativně „pomalými“ rychlostmi, při nichž se časoprostorová trigonometrie projevuje jen velmi málo.
Pro daný příklad lze proto použít i tradiční newtonovské vztahy (viz Limitní zjednodušení pro „pomalé“ děje), které vypočtou dopadovou rychlost meteoru ve velmi podobné hodnotě 0,002060684 (617 777,5 m/s) – rozdíl je v řádu 10‒7 pro interní rychlost a 10‒6 pro rychlost externí.
V naší Sluneční soustavě se tudíž můžeme na Newtona spolehnout s poměrně velmi vysokou přesností (na hranicích dnešních metrologických technologií)!

