3.6.12 KOSMICKÉ RYCHLOSTI 4D ČASOPROSTORU

S ohledem na 4D časoprostor o němž Newton neměl tušení (objevil jej až Minkowski) a interpretaci časoprostoru v rámci TČ – je třeba poupravit vztahy pro výpočet tzv. „kosmických rychlostí“:

Pro výpočet 2. kosmické rychlosti je určující gravitační potenciál, který přímo definuje časoprostorový úhel:

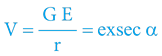
Přičemž máme na paměti, že funkci exsec na kalkulačkách nenajdeme a je praktičtější ji přepočítat na funkci cos, respektive na inverzní funkci arccos:

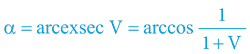
Následně je snadné dopočítat 2. kosmickou rychlost – z pohledu externího pozorovatele v barycentru i z pohledu interního účastníka pohybu:

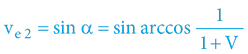
Výšeuvedené lze vyjádřit i jako alternativní (pythagorejské) tvary rovnic:

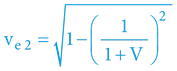
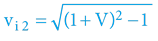
Výpočet 1. kosmické rychlosti (pro interního i externího pozorovatele) snadno dopočítáme – dle obecného principu:

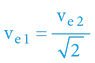
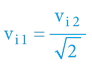
Pro běžné gravitační síly (v blízkém vesmíru) dosahují objekty relativně nízkých rychlostí, respektive nízkých časoprostorových úhlů – kontrakce/dilatace času se zde projevuje téměř neznatelně, respektive teprve v dlouhých časových úsecích se časové disproporce „nasčítají“ tak, aby byly zřetelné.

Jak jsme již vypočítali v předchozím hypotetickém příkladu – meteor z okraje Sluneční soustavy dopadne na Slunce tak „malou“ rychlostí, že rozdíl v měření rychlosti interním a externím pozorovatelem bude „jen“ 1 m/s.

Výšeuvedené taktéž demonstruje, proč jsme se v naší Sluneční soustavě dosud mohli spolehnout na zjednodušené Newtonovy zákony – ani mise Apolla na Měsíc nepotřebovala ke svému úspěchu jakékoliv korekce vzhledem k dilataci času.

V tomto ohledu (v rámci gravitačních sil naší Sluneční soustavy) je Newtonův vzorec pro výpočet kosmických rychlostí taktéž dobře použitelný jako výšeuvedené vzorce – dává de facto stejné výsledky – jeho nepřesnost je v reáliích naší SS poměrně malá.

Newtonův vzorec:

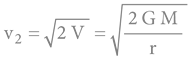
Zde těží vesmírná mechanika blízkého vesmíru opět z faktu, že pro malé úhly jsou sinus, tangenta i oblouková hodnota úhlu v radiánech (arcus) de facto totožné!

Taktéž je třeba zdůraznit – že výšeuvedené vztahy jsou „idealizované“ pro situace, kdy pohybující se těleso má zanedbatelnou hmotnost ve srovnání s centrálním tělesem, k němuž kosmické rychlosti vztahujeme. V takovém případě můžeme zanedbat symetričnost pohybů a pohled „nehybného centrálního“ obra lze považovat za externí optiku, zatímco pohybujícímu tělesu náleží optika interní.

Jakmile by uvedená podmínka neplatila – matematika se začíná komplikovat – pohyb „centrálního“ tělesa již nelze zanedbat a je třeba použít výpočty dle předchozí kapitoly – viz Gravitační problém 2 těles ve 4D časoprostoru.

Taktéž je důležité si připomenout, že matematika 2. kosmické rychlosti pro „únik“ z gravitačního pole je totožná (reciproční) pro situaci, kdy počítáme dopadovou rychlost tělesa padajícího „z nekonečna“!