PŘÍBĚH MIONU …
V předchozích kapitolách jsme užili příklad mionů. Tentokrát se na příběh mionů zaměříme podrobněji – je k tomu dobrý důvod: Příběh mionů je realitou – neustále probíhajícím experimentem přírody, který nám znovu a znovu dává jednoznačný důkaz existence dilatace času (nikoliv však důkaz platnosti TR):
Miony jsou nestabilní elementární částice se záporným nábojem, jejichž poločas rozpadu je v laboratorních podmínkách cca 2,2·10‒6 sekundy, a následně se rozpadají na jiné částice. Uvedený čas je však pouze „poločas rozpadu“ – znamenající, že za tento čas zanikne polovina částic – zbývajících částic za stejný čas opět polovina zanikne, a tak znovu a znovu – jde o logaritmický úbytek. Desetina částic přežije čas 7·10‒6 sekundy, a to je pořád obrovské množství částic pro jejich spolehlivou detekci.
V přírodě vznikají miony neustále v horní vrstvě atmosféry (ve výši cca 15 km) díky proudu slunečního záření, které jim při vzniku zajišťuje téměř rychlost světla 0,995 c ≅ 2,985·108 m/s.
A právě výšeuvedená fakta nám dávají nezvratný důkaz o dilataci času. Dostatečné množství mionů by totiž do detektorů na zemském povrchu nikdy nemohlo doletět, kdyby nebylo dilatace času. Za časový úsek 7·10‒6 sekundy by miony (při rychlosti 2,985·108 m/s) uletěly maximálně 2 km – k zemskému povrchu by nedoletěly!
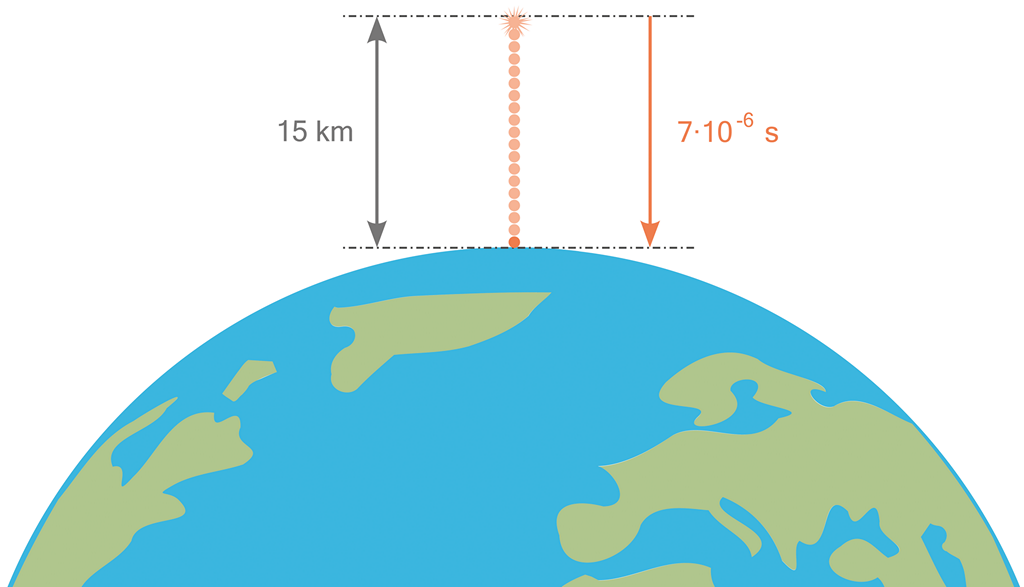
Obrázek 68:
Příběh mionů je neustálým důkazem matky přírody o tom, že dilatace času je objektivní realitou.
My však v pozemských laboratořích detekujeme takové množství mionů, že (z našeho pozemského pohledu) od okamžiku jejich vzniku v atmosféře „přežily“ v dostatečném množství minimálně 70·10‒6 sekundy. Jinými slovy: Při 99% rychlosti světla žijí miony z pohledu externího pozorovatele 10× déle, což jim umožní doletět až k zemskému povrchu (dráhu v délce 15 km). Tento přirozený experiment matky přírody byl již mnohokrát vědecky potvrzen, je neustále zpřesňován a velmi dobře souhlasí s matematikou pro dilataci času.
V minulé kapitole jsme objasnili, že v důsledku 2. postulátu je v TR dilatace času doprovázena svým jednovaječným dvojčetem – kontrakcí délek:
Není totiž pochyb, že z interního pohledu mionu je jeho život stále stejně krátký – mion má jen 10% pravděpodobnost, že se dožije 7·10‒6 sekundy (takový mion je z pohledu ostatních mionů dlouhověký stařík). Jak je tedy možné, že desetina mionů přesto doletí až na povrch Země? To, že mion na Zemi doletěl, je nezpochybnitelný fakt – detektory na zemském povrchu jej zaznamenaly. Jak to lze vysvětlit?
Jsou jen dvě možnosti:
Buď mion letěl desetkrát větší rychlostí 9,95 c ≅ 29,85·108 m/s, nebo se mu vzdálenost z horních vrstev atmosféry na povrch Země desetkrát „scvrkla“ (na pouhých 1,5 km). Který scénář je ten pravý?
TR má jasno:
Rychlosti jsou unifikované a jednotné (stejné z pohledu interního i externího pozorovatele), navíc jsou nadsvětelné rychlosti „zakázány“ – takže volíme kontrakci délek! Pakliže nám experimenty potvrdily, že dilatace času existuje (jedna ze základních veličin mezinárodní soustavy SI se chová bláznivě), tak proč by se bláznivě nemohla chovat i délka? Hlavní je, aby ta vedlejší (odvozená) počitatelná veličina rychlosti v = s/t zůstala stejná (a nepřekročila rychlost světla).
Výšeuvedená argumentace je též důvodem, proč jsou experimenty s miony v mnoha odborných pramenech deklarovány jako „důkaz“ existence kontrakce délek.
Při popisu kinematických jevů tedy popíšou stejný jev dva pozorovatelé rozdílně, v závislosti na jejich pozici vůči pohybujícímu se objektu. Demonstrujme si tvrzení TR na příběhu mionů:
Tvrzení 1:
Pozoruji-li pohybující se mion ze svého pozemského stanoviště, pak veškeré děje pohybujícího se mionu pozoruji zpomalené – čas pohybujícího se mionu plyne pomaleji nežli můj – hodiny pohybujícího se mionu tikají pomaleji vůči mým hodinám. Umím dopočíst rychlost pohybu mionu v = s/t a vždy dopočtu podsvětelnou rychlost (0,99 c).
Tvrzení 2:
Na základě svých pozorování, principů TR a matematiky umím dopočítat, že:
Z pohledu mionu čas plyne stále standardním tempem (hodiny tikají korektně), avšak prostorová délka (dráha) je ve směru pohybu zkrácena vůči mnou naměřené délce – metr je ve směru pohybu pro mion kratší vůči mému standardnímu metru. Dopočtu-li trajektorii, umím taktéž dopočítat rychlost pohybu mionu v = s/t a vždy dopočtu podsvětelnou rychlost – dopočtu shodnou hodnotu rychlosti mionu jako ve svém předchozím tvrzení (0,99 c).
Souhrnně (z pohledu Země):
Čas mionu tiká pomaleji nežli „normální“ čas Země a stejnou měrou je ve směru pohybu mionu vesmír zkrácen vůči „normálním“ vzdálenostem.

