3.6.16 RESUMÉ KE GRAVITACI
Gravitační zákon symetrického pohybu (GZSP):
Hmota objektů není prostorově ohraničená – hmota každého objektu prostupuje ve formě gravitačního pole celým vesmírem.
Hmota generuje v prostoru gravitační potenciál, který klesá nepřímo úměrně vzdálenosti. Tento gravitační potenciál indukuje v okolních hmotných objektech kinetickou energii, respektive indukuje jejich pohyb. Tomuto jevu říkáme gravitace.
V důsledku gravitace se lokálně izolované objekty pohybují 4D Euklidovským prostorem symetricky vůči společnému hmotnému středu, který je zachováván.
Gravitace je záhadný a v mnoha ohledech dosud nepoznaný fenomén – nechápeme gravitaci zcela a leccos nám uniká. Nicméně – mnohé o gravitaci přeci jen víme:
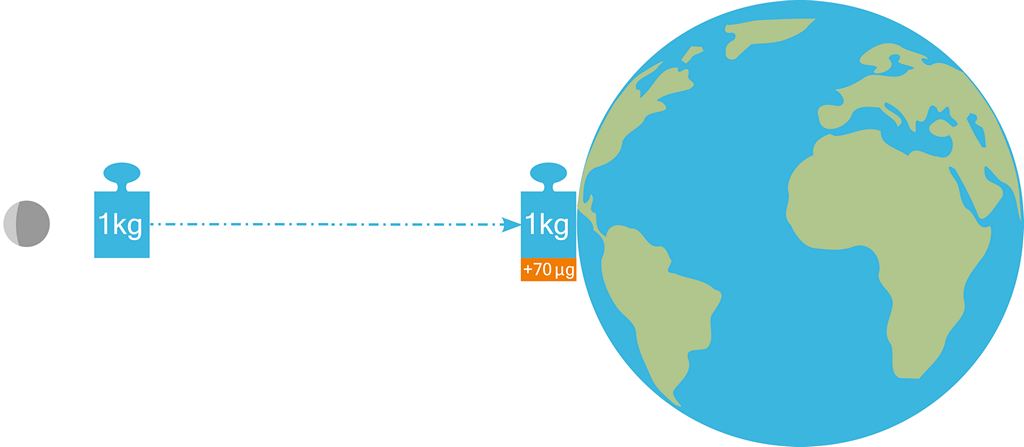
Umístíme-li v „prázdném“ vesmírném vakuu (společného) barycentra Země a Měsíce kilogramové závaží (například si vypůjčíme kilogramový etalon z Paříže) – setrvá po určitou dobu na svém místě v prostoru – nebude padat ani k Zemi, ani k Měsíci.
Na Zemi však takřka neustále dopadá z vesmíru hmota ve formě meteoritů a vesmírného prachu, což časem nepatrně změní gravitační rovnováhu působící na kilogramové závaží – a to započne padat směrem k Zemi.
Ve výsledku dopadne „kilogramové“ závaží na Zemi rychlostí cca 11 km/s (zanedbáme-li odpor atmosféry naší planety), respektive na Zemi dopadne cca 1,0000000007 kg hmoty!
Na Zemi se tak vrátí nejen původní 1 kilogram, ale i 7·10‒10 kg navíc – není problém tuto energii (hmotu) navíc nějak zužitkovat – přeměnit ji při dopadu v teplo či v elektrickou energii.
Oněch nepatrných 70 µg hmoty (energie) přitom předala původnímu závaží vesmírná „prázdnota“ – které naivně říkáme „vakuum“!
Obrázek 146:
Jak mohla prázdnota stvořit hmotu?
V reálném světě (reálném vesmíru) se při pohybu objektů „pustinami“ vesmírného vakua mění energie (tedy hmotnost) těchto objektů v závislosti na gravitačním potenciálu lokálních masivních těles.
Zcela analogicky se též mění energie (hmotnost) elektromagnetického záření (fotonů), respektive frekvence záření – což nazýváme gravitačním rudým (či modrým) posuvem.
Z výšeuvedeného plyne závěr, že vakuum není vakuum – vakuum není nikdy prázdné!
Vesmírné vakuum je médium – je dalším skupenstvím hmoty! V každém místě vesmírného vakua je přítomno gravitační pole (rozdílného potenciálu), jehož energetická „hustota“ definuje pohyb ostatní hmoty (látky i polních částic typu foton).
Fakt, že netušíme vůbec nic o způsobu gravitační interakce (jaké částice předávají onu energii a hmotnost?) – na výšeuvedených faktech nic nemění!
Vesmírné vakuum (éter) je dalším skupenstvím hmoty!
Vesmír je jedním uceleným hmotným objektem – není prázdným prostorem, v němž se pohybuje nespočet „samostatných“ hmotných objektů. Představa nekonečné prázdnoty (vakua), v níž se občas objeví pár atomů, které se časem shlukují do planet a hvězd … je historickým přežitkem!
Tvrdíme, že optickými a radiovými teleskopy mapujeme vesmírnou hmotu – ale ve skutečnosti mapujeme látku a elektromagnetické záření, nikoliv celkovou hmotu – viz Hmota.
Zatímco látka je ve vesmíru přítomna relativně řídce (ve shlucích), hmota je ve vesmíru všudypřítomná a liší se pouze její koncentrace, která ve výsledku určuje souhrnný gravitační potenciál v daném místě vesmíru.
Gravitační pole je „pojivem“, které shluky látky váže pospolu – pojivem, které má svoji energii (a tedy i hmotnost)!
Relace mezi hmotou a gravitací je podobná relaci elektřiny a magnetismu:
Hmota produkuje v okolním prostoru gravitační pole, jehož potenciál klesá nepřímo úměrně vzdálenosti (1/r) – působí do nekonečna (byť s klesající intenzitou). Takový gravitační potenciál však zpětnou vazbou působí na všechnu ostatní hmotu ve vesmíru (nejen na látku) tím, že oné okolní hmotě „indukuje“ pohyb, respektive kinetickou energii (a tedy i hmotnost)!
Energie objektů (a jejich hmotnost) tedy není vlastností objektů samotných!
Hmotnost (energie) objektů je dána souhrnnou „indukcí“ gravitačního potenciálu veškeré vesmírné hmoty. Je-li hmotný objekt v blízkosti jiných masivních objektů (např. centra galaxií) – je v silnějším gravitačním potenciálu (nežli v podmínkách naší SS) a takový objekt bude mít větší energii (větší hmotnost). Přírůstek této energie (hmotnosti) bude dán kinetickou energií – ať již půjde o „pád“ k centru galaxie či orbitální trajektorii, anebo u fotonů (které jsou de facto samy o sobě kvanty „čisté“ kinetické energie) bude takový přírůstek energie přímo zvyšovat primární energii elektromagnetického záření (růst frekvence).
Na tomto místě můžeme pouze konstatovat, že zůstává mnoho nezodpovězeného nad otázkou „Co je to vlastně energie?“. Učebnicové definice mnoho nenapoví a ani TČ nemá v tomto ohledu zcela exaktní názor. V kontextu TČ proto nabízíme pouze opatrnou a skromnou definici: Energie je schopnost měnit pohybový stav hmoty.
Celková energie (respektive celková hmotnost) je u reálných hmotných objektů definována celkovým rozložením hmoty vesmíru. V „hustším“ vesmíru bude energie, respektive hmotnost, respektive pohyb každého objektu větší – v „řídkém“ vesmíru tomu bude naopak.
Nic smysluplnějšího v tuto chvíli o našem vesmíru říci nedokážeme. V každém případě se však musíme rozloučit s představou, že energie či hmotnost „sídlí“ přímo v daném „viditelném“ či „hmatatelném“ objektu.
Hmotnost předmětů nám tak sděluje mnohé o fyzikální podstatě zkoumaného objektu, zároveň nám však sděluje mnohé o našem vesmíru!
Kopneme-li nohou do čehokoliv – registrujeme setrvačnost (setrvačnou hmotnost) – hmotnější předmět odletí do kratší vzdálenosti a nás bude více bolet palec u nohy. Zvedáme-li břemeno ze země – registrujeme tíhu (tíhovou hmotnost) – hmotnější předmět nás vyčerpá více.
V obou případech jde však o projev téhož – souhrnné gravitační působení všech objektů ve vesmíru (jejich gravitační potenciál) definuje energii (hmotnost) všech objektů (děje se účastnících), a tím pádem definuje i energii, kterou je nutné vynaložit, chceme-li změnit pohybový stav těchto objektů (ať již jde o setrvačnost, či tíhu).
Nikdy tudíž nepohneme pouze jedním hmotným objektem – pohyb je vždy energeticky (hmotnostně) symetrický:
Vystřelíme-li z pušky – zpětný ráz eliminuje pohyb kulky – těžiště uskupení (střelec + puška + náboj) se nezmění. Zvedneme-li činku – část našeho těla a část země (na níž stojíme) se pohne opačným směrem takovým způsobem, že těžiště zeměkoule se opět nezmění.
V obou případech je ona energie se změnou spojená (odpor, který tělesa kladou změně svého pohybového stavu v prostoru) definovaná celkovou „hustotou“ gravitačního potenciálu v daném místě vesmíru – v hustší části vesmíru bude „odpor“ silnější – což budeme interpretovat jako vyšší hmotnost. Vše výšeuvedené je přitom poněkud zjednodušené – reálně je vše propojené se vším:
Zvedáme-li činku, pohybujeme ve skutečnosti všemi objekty vesmíru!
Pouze barycentrum (hmotný střed) vesmíru zůstává neměnné – protože veškerá hmota vesmíru je propojená gravitačním polem (prostřednictvím vakua) – jde o jeden objekt!
S pohybem činky se opačným směrem nepatrně přesune těžiště vzpěrače i těžiště Země – a tím se ještě nepatrněji pohne těžiště Slunce – a tím ještě nepatrněji těžiště naší galaxie – a tak dále, a tak dále … protože rozložení hmoty ve vesmíru je vždy symetrické a „vyvážené“.
A protože gravitační potenciál klesá nepřímo úměrně vzdálenosti – je „odpor“ hmoty proti změně jejího pohybového stavu (setrvačnost) definován poměrem hmoty vesmíru a objemu vesmíru (za předpokladu homogenního rozložení hmoty ve vesmíru, což nám snad potvrzuje naše zkušenost, že setrvačnost není směrově závislá).
Energetická hustota současného vesmíru tedy definuje odpor proti změně pohybového stavu – definuje setrvačnost – definuje energii (a tedy i hmotnost) všech objektů ve vesmíru!
Mohli bychom jít v těchto úvahách ještě dál – ale již bychom se dostali za hranice vědeckého myšlení – šlo by o spekulace a fantazírování.
Netušíme téměř nic o rozměrech a celkové energii vesmíru (tušíme jen hrubé údaje o viditelné části vesmíru) – nemůžeme dělat v tomto ohledu jakékoliv výpočty. Principálně však musíme přijmout fakt, že energie (hmotnost) těles je definována gravitačním působením všech ostatních těles vesmíru, přičemž působení lokálních hmotných uskupení ovlivňuje energii těles sekundárně (a opět úměrně vzdálenosti).
Proto mají planety blíže ke Slunci větší orbitální rychlost – a tudíž větší energii (a tudíž větší hmotnost). Proto má paprsek světla letící směrem ke Slunci více energie (foton větší hmotnost), respektive vyšší frekvenci. Proto pozorujeme gravitační rudý posuv, refrakci (ohyb) světla i efekt „gravitační čočky“.
Gravitace je projevem Zákona symetrického pohybu ve 4D prostoru za situace, kdy hmotné objekty nejsou prostorově ohraničené, jejich energie (hmotnost) sahá do nekonečna (potenciál klesá nepřímo se vzdáleností) a zároveň je tato energie sdílena ostatními hmotnými objekty!
Musíme přestat zjednodušovat:
Vesmír není tvořen hmotnými body ani hmotnými koulemi!
Vesmír je tvořen jedinou společnou sdílenou hmotou, která je vzájemně energeticky (hmotnostně) propojená a která při svém neustálém pohybu respektuje GZSP tak, aby „těžiště“ vesmíru zůstalo vyvážené.
Možná je celý náš vesmír jen „malou“ plovoucí kuličkou na hladině v Petriho misce a nějaký „ufounský“ učitel na ní právě demonstruje žákům Zákon zachování hybnosti, respektive Zákon symetrického pohybu.
Kdo ví?
Ono známé „vše souvisí se vším“ je možná nejpřesnější vyjádření podoby našeho vesmíru:
V reálném světě – kde vakuum v každém koutě vesmíru zprostředkovává hmotným předmětům indukci energie, a tedy i hmotnosti – tělesa se (bez působení síly) pohybují daným prostorem po křivkách, jejichž trajektorie je definována lokálním gravitačním potenciálem všech okolních těles – a to tak, aby pozice hmotného středu lokálního uskupení objektů zůstala neměnná (v rámci množiny lokálně izolovaných hmotných objektů – vhodně zvolených s vědomím, že vliv ostatních hmot ve vesmíru není možné nikdy zcela eliminovat).
V důsledku gravitace – se tedy objekty v reálném světě nikdy nepohybují „rovnoměrným přímočarým pohybem“ ani po dokonalých kuželosečkách – svůj přirozený pohyb podřizují principu symetrie – aby „těžiště“ lokálního uskupení objektů zůstalo ve vesmíru zachováno!
Výšeuvedené (mimo jiné) též znamená, že „model“ naší Sluneční soustavy není ani geocentrický, ani heliocentrický! V reálném světě je pohyb vždy symetrický (nikdy se nepohybuje pouze jeden objekt osamoceně), a protože mírou pohybu je hybnost – touto perspektivou můžeme prohlásit:
• Geocentrický model SS je z 99,5 % mylný!
• Heliocentrický model SS je z 50 % mylný (z 50 % je korektní)!
• Model naší SS je barycentrický!
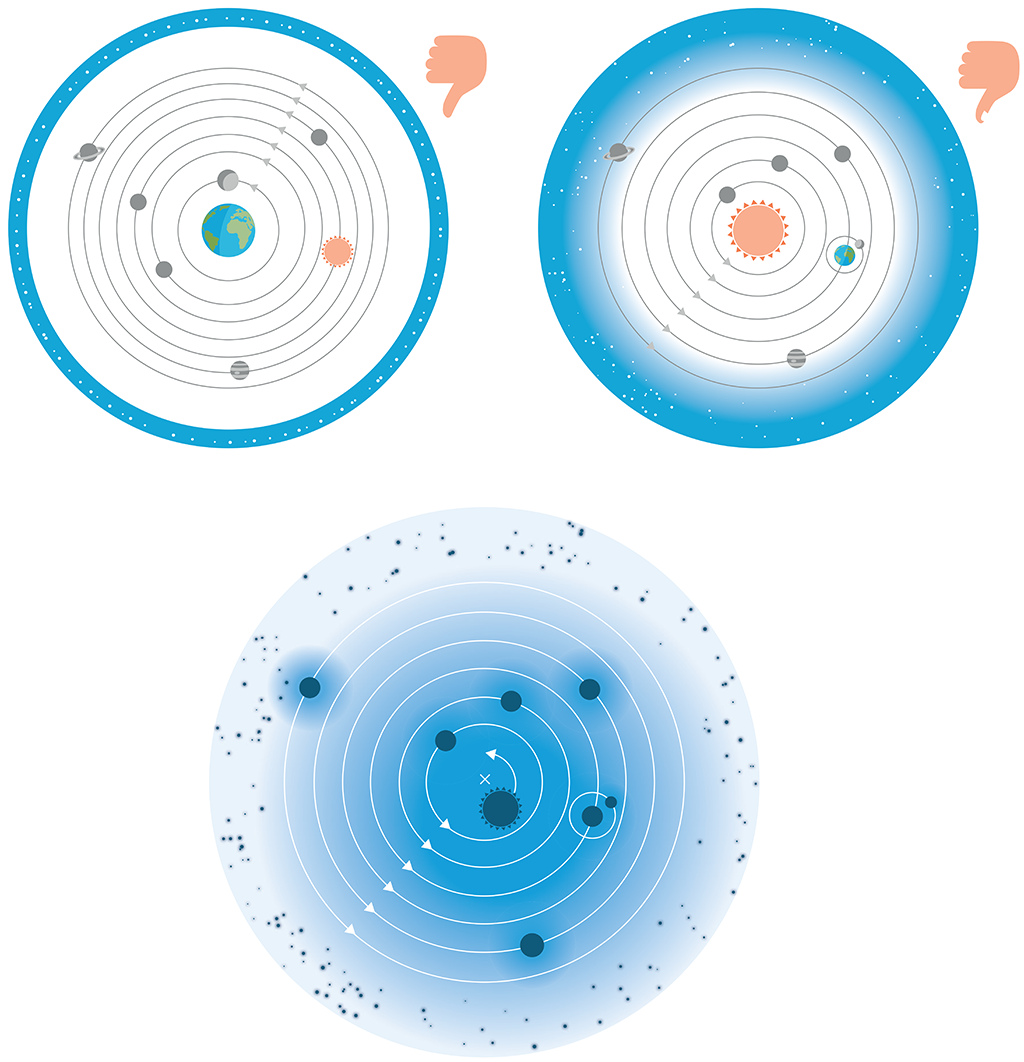
Obrázek 147:
Naše Sluneční soustava je barycentrická!
Co lze tedy souhrnně říci o gravitaci?
Globální (souhrnná) úroveň gravitačního potenciálu (v kontextu energetické hustoty vesmíru) definuje primární energii (hmotnost) objektů.
Tato energie objektů však není prostorově ohraničená – s klesající intenzitou sahá do nekonečna a lokálně indukuje pohyb všem dalším okolním objektům – tomuto jevu říkáme GRAVITACE!
Vlivem gravitace se hmota ve vesmíru shlukuje do lokálního uskupení objektů, jež (dle výšeuvedeného principu) vytváří lokální radiální gravitační potenciál, který je přímo úměrný energii onoho hmotného uskupení a nepřímo úměrný vzdálenosti.
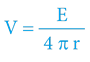
Rozdílné hladiny tohoto lokálního (radiálního) potenciálu indukují pohyb okolních objektů, respektive definují exsekantu časoprostorového úhlu, respektive rychlost pohybu objektů vůči barycentru hmotného uskupení objektů (ať již optikou pohybujícího se objektu, anebo optikou nehybného barycentra – vzhledem k Zákonu 4D prostoru).

ve = sin α
vi = tan α
Lokální rozdíl gravitačního potenciálu hmotnostně dominujícího tělesa tak přímo definuje přírůstek/úbytek kinetické energie okolních objektů, respektive Ek/E0.
I toto působení je samozřejmě vzájemné (dle Zákona symetrického pohybu), u hmotnostně dominantního tělesa lze jeho pohyb (více/méně) zanedbat.
Základem vztahu pro výpočet gravitačního potenciálu je vzorec pro výpočet plochy koule!
Gravitační potenciál je souhrnná veličina – přímo kvantifikující přírůstek energie vůči prvotní energii tělesa, jež se pohybuje mezi jednotlivými hladinami s rozdílnou intenzitou gravitačního pole. Jde o bezrozměrnou veličinu!
Celkový gravitační potenciál tak přímo definuje (mimo jiné) i 2. kosmickou rychlost, respektive časoprostorový úhel pohybu, který je nutný k trvalému vymanění se z gravitačního vlivu daného objektu – obrácenou perspektivou definuje míru pohybu při dopadu tělesa „z nekonečné výšky“.
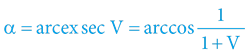
Sloučením s předchozími vztahy pak dostaneme rozličné tvary rovnic pro 2. kosmickou rychlost (KR) „osamoceného“ (hmotnostně dominujícího a centrálně symetrického) objektu:
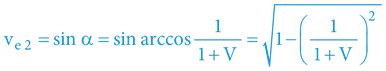

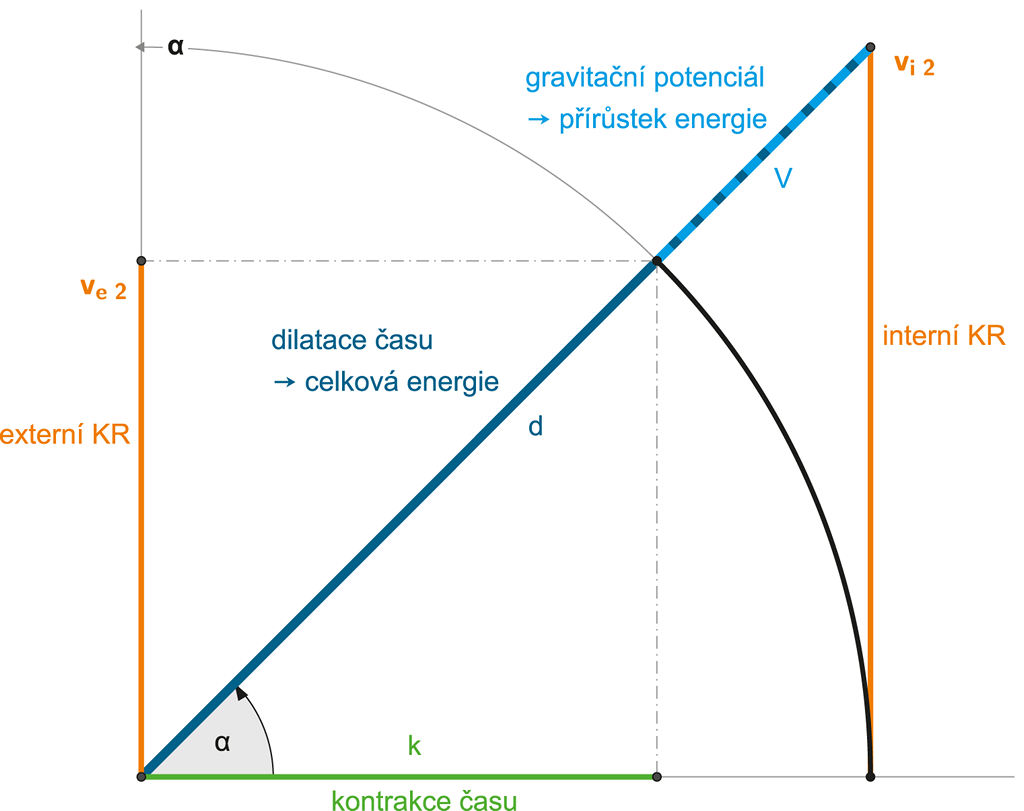
Obrázek 148:
Gravitační potenciál definuje kosmické rychlosti.
Výpočet 1. kosmické rychlosti, respektive rychlost stabilní kruhové orbity „osamoceného“ (hmotnostně dominujícího a centrálně symetrického) objektu snadno dopočítáme – dle obecného principu:
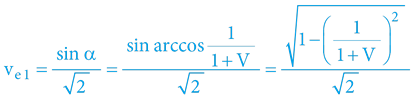
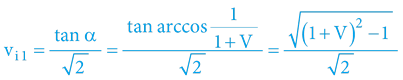
Analogicky lze odvodit i vtahy pro výpočet oběžné doby stabilní kruhové orbity, jejíž obvod vyjádříme jako O = 2πr externí i interní optikou:
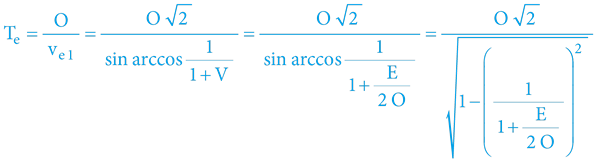
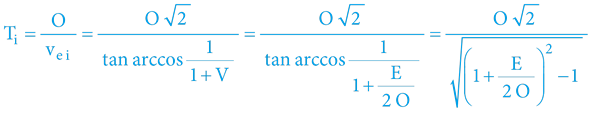
Zjednodušený Newton/Keplerovský vzorec
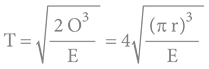
bude platit jen přibližně a jen pro malé rychlosti, respektive jen pro slabá gravitační pole!
Výšeuvedená matematika „kosmických rychlostí“ se vztahuje na „běžné“ hmotné objekty, mající „látkový“ charakter, jejichž hmotnost je vůči hmotnosti centrálně symetrického hmotného tělesa zanedbatelná!
Elektromagnetické záření (světlo) podléhá jiné matematice:
Fotony jsou kvanty „čisté“ (kinetické) energie, prostorem se fakticky pohybují nekonečnou rychlostí (jednotkovou rychlostí z externího pohledu). V jejich případě tudíž gravitační potenciál okolních těles nemění rychlost pohybu, ale přímo ovlivňuje primární energii záření, respektive jeho frekvenci. Projevem tohoto fenoménu je Gravitační rudý posuv či Gravitační modrý posuv:
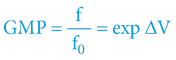
Je-li ΔV kladné (záření směřuje do barycentra), pak jde o GMP (frekvence a energie záření roste), je-li ΔV záporné (záření směřuje od barycentra), pak jde o GRP (frekvence a energie záření klesá).
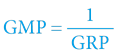
GRP či GMP je tedy přímo definován exponenciálou gravitačního potenciálu. Inverzně mohou tuto závislost použít astrofyzikové – a dle naměřeného posuvu (GRP) určit hodnotu gravitačního potenciálu vzdáleného objektu, z něhož světelné záření pochází. V takovýchto situacích můžeme gravitační potenciál v místě pozorování (Země) považovat za nulový a použít rovnici:
V = ln (GRP)
Pro veškerou hmotu samozřejmě platí, že objekty se pohybují (i vlivem gravitace) vždy tak, že se zachovává společné barycentrum všech objektů – vzhledem k Zákonu symetrického pohybu.
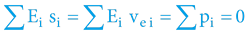
Lokální distribuce hmoty v „blízkém“ vesmíru tedy určuje trajektorii pohybu těles (vůči lokálnímu barycentru). Taktéž určuje částečně změny v celkové energii (hmotnosti) těles, respektive změny ve frekvenci elektromagnetického záření.
Přestože mnohé o gravitaci zůstává utajeno (mechanismus gravitační interakce, velikost i energie vesmíru, …) – výšeuvedené spolehlivě popisuje pozorovanou podobu vesmíru – nic víc není třeba, respektive vše navíc pouze komplikuje poznání podstaty gravitace:
Zakřivení časoprostoru, Černé díry i Temná hmota jsou pouhými nepodloženými spekulacemi, jež jsou možná přínosné pro vědecko-fantastickou literaturu – vědecký pokrok však brzdí a vědecké myšlení „zatemňují“.

