3.6.7 STÁČENÍ MERKUROVA PERIHELIA
„Co si myslíme, že víme, nám znemožňuje se něco naučit!“
Claude Bernard
Již v předchozích kapitolách jsme zmínili matematika jménem Urbain Le Verrier, který na základě anomálií dráhy Uranu předpověděl existenci planety Neptun. Tento vynikající vědec následně pokračoval v hledání dalších „nesrovnalostí“ trajektorií planet a objevil je u první planety – Merkur. Verrier je zpočátku opět přisuzoval existenci dosud neobjevené planety (dostala virtuální jméno Vulkan), avšak tentokrát se mýlil – žádná další planeta objevena nebyla.
Problém je znám pod názvem „Stáčení (precese) Merkurova perihelia“.
Oběh Merkuru, jehož dráha je značně excentrická (a proto se poměrně dobře stanovuje perihelium), vykazuje největší odchylky od trajektorie dokonalé elipsy.
Elipsa Merkuru se zřetelně stáčí (po směru jeho orbity) – a to více, nežli uměl Verrier objasnit svými „poruchovými vzorci“.
Verrier provedl své výpočty „planetárních odchylek“, respektive „poruchových funkcí planet“ – započetl vliv vlastní trajektorie Země (odkud Merkurovu trajektorii pozorujeme) i vliv gravitace ostatních planet.
Verrier dokázal svými vzorci objasnit naprostou většinu pozorované precese (99,3 % pozorované odchylky), avšak 0,7 % precesního pohybu zůstalo nevysvětlitelnou „chybou“.
Ve výsledku se tak Verrier dopočítal k chybě Merkurovy precese v hodnotě 38“/100 let a později (1895) matematik Simon Newcomb jeho odchylku „přepočítal“ na 43“/100 let.
Právě tato hodnota odchylky je v neměnné výši udávaná v odborné literatuře dodnes jako fenomén zakřivení časoprostoru. Proč?
Na počátku 20. století Einstein představil světu svou TR a mimo jiné předložil matematický vzorec, který přesně zapadl do chybějících čísel a plně „pokryl“ onu odchylku 43“ – viz kapitola Stáčení perihelia v první části této knihy.
Teoretickým fundamentem Einsteinova vzorce byla jeho OTR, respektive zakřivení časoprostoru – jež je (dle OTR) v blízkosti masivního Slunce již natolik veliké, že „přibližná“ Newtonova gravitace zde již nemůže být použita – řešením je pouze TR, jež je (údajně) řešením obecným. Ve zbytku SS je nicméně gravitace „normální“, a proto zde můžeme spolehlivě používat Newtonovskou fyziku.
V tomto duchu lze velmi stručně (a velmi zjednodušeně) charakterizovat Einsteinovo „řešení“ Merkurovy precese.
Co dodat?
Že řešení OTR je účelovým řešením „ad hoc“ – daný problém je totiž nepoměrně složitější:
• Reálné stáčení perihelia je astronomicky obtížně a nepřesně měřitelné, respektive kolísá v čase. Z principu TR (zakřivení časoprostoru) by přitom měla být precese konstantní.
• V kontextu dnešních astronomických dat činí průměrná (dlouhodobá) odchylka spíše 40“/století.
• Výpočet zcela ignoruje trajektorii Slunce – na Slunce hledí „heliocentricky“, považuje jej za nehybné a nikterak nezohledňuje měnící se polohu Slunce – ignoruje SIM – ignoruje tedy 50 % pohybu v naší SS.
• Výpočet ignoruje zploštění Slunce – považuje gravitační pole Slunce za radiálně homogenní, respektive rotační zploštění hmoty Slunce považuje za zanedbatelné.
• Výpočet ignoruje slapové síly z centra naší galaxie.
Mimochodem – totožný vzorec (jako TR) pro „objasnění“ Merkurovy precese vyprodukoval 17 let před Einsteinem německý učitel fyziky Paul Gerber, a to bez „zakřivení časoprostoru“ (v tomto ohledu bývá Einstein dokonce někdy napadán za plagiátorství). Bez ohledu na to, kdo koho kopíroval, se však nejspíš mýlili oba!
Na základě výšeuvedeného je zřejmé, že „potvrzení platnosti TR“ je v případě anomálie precese Merkurova perihelia teoreticky i empiricky neopodstatněné!
Již samotná existence pohybů Slunce (prvně kvantifikovaná 1965) činí výpočet „poruchových funkcí“ všech Einsteinových předchůdců i současníků prakticky nefunkčním.
V reáliích naší Sluneční soustavy se v důsledku nezanedbatelného pohybu Slunce rozchází s teorií nejen skutečná vzdálenost Merkuru od Slunce, ale i vzdálenost ostatních planet od Slunce (především Jupitera a Saturnu), které taktéž stáčejí svou gravitací Merkurovu „elipsu“. Jde o matematickou multizávislost, která není řešitelná analyticky – pomocí (relativně) jednoduchých „poruchových funkcí“ založených na zjednodušených eliptických orbitách (ježto jsou založeny na nehybném Slunci a zanedbávání dalších vlivů).
Korektně lze proto reálnou situaci v naší SS řešit pouze numericky (hrubou výpočetní silou počítačů) s použitím Gravitačního zákona symetrického pohybu – reflektujícího pohyb všech těles – s nutností ignorovat „středověké“ představy o centrálním nehybném Slunci a o „dokonalosti“ eliptických trajektorií.
Primárním problémem kauzy „Stáčení Merkurova perihelia“ je však problém „systémový“ – rezignace na jednotné a ucelené vědecké myšlení:
Ačkoliv „poruchy“ (rozpory s naším teoretickým matematickým modelem) v oběžných trajektoriích nebeských těles nám ve skutečnosti sdělují informace o distribuci (rozložení) hmoty v našem vesmíru, věda tyto informace ignoruje a raději je interpretuje jako „zakřivení časoprostoru“, a když ani to nepomáhá, pak jako přítomnost „Temné hmoty“.
V případě Merkuru bychom se na základě přesného sledování jeho trajektorie mohli dozvědět více o Slunci – jeho skutečném (hmotnostním) tvaru, eventuálním zploštění a blíže bychom mohli analyzovat pohyby Slunce (SIM) kolem barycentra SS.
Jak jinak může lidstvo poznat skutečnou orbitu, podobu a tvar Slunce?
Právě odchylky orbitálních drah (planet či umělých satelitních družic) by nám mohly dát odpověď …
Je přitom pozoruhodné (a úsměvné), že v případě naší vlastní planety Země se věda chová smysluplně a vědecky. Umíme totiž použít „poruchy“ satelitů na orbitě Země ke zjištění nerovnoměrného rozložení hmoty Země:
Protože veškeré výpočty nebeské mechaniky jsou založeny na idealizovaném předpokladu (centrální hmotné těleso je dokonalá koule produkující homogenní radiální gravitační potenciál) – odchylky reálné trajektorie na orbitě Země od jejich teoretického předpokladu chápeme jako šanci ke zjištění reálných proporcí naší planety (jež samozřejmě není ani kulatá, ani se neskládá z unifikovaného (stejně hustého) materiálu – a tudíž neprodukuje homogenní radiální gravitační pole). Tyto nepravidelnosti jsou výraznější na nižších oběžných drahách satelitů, se stoupající vzdáleností se snižují – související vesmírné programy proto používají družice na těch nejnižších orbitálních drahách Země (viz podobnost s Merkurem).
Tohoto vědeckého programu se účastní především projekty ESSP (Earth System Science Pathfinder) a GRACE (Gravity Recovery And Climate Experiment) v kooperaci USA (NASA) a Německa. Evropská agentura ESA přispívá svým projektem GOCE.
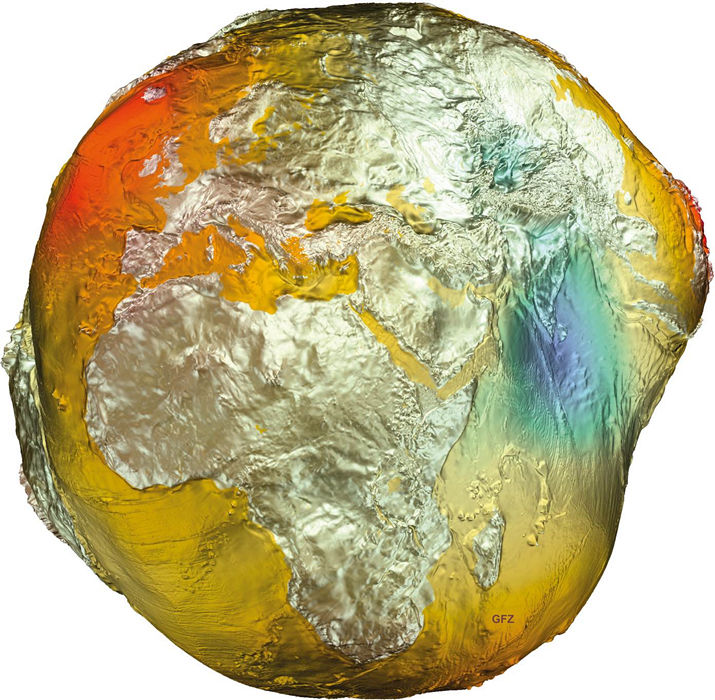
Obrázek 133:
Zemské gravitační pole – není vůbec kulaté! (zdroj: GFZ)
Na Zemi nám vědecké myšlení pomohlo interpretovat poruchy orbitálních trajektorií jako nové informace o zploštění Země (vlivem rotace), deformaci Země (vlivem slapových sil Měsíce a Slunce), tvaru zvlnění povrchu (pohoří, údolí, kanály, kaňony, …), hustotě rozložení hmoty (umíme předpovídat složení hornin), síle přílivu a odlivu (sledujeme globální stěhování vody na planetě), dynamice tání ledu v polárních oblastech, a dokonce umíme zaznamenat i poruchy orbity v důsledku největších staveb vytvořených člověkem!
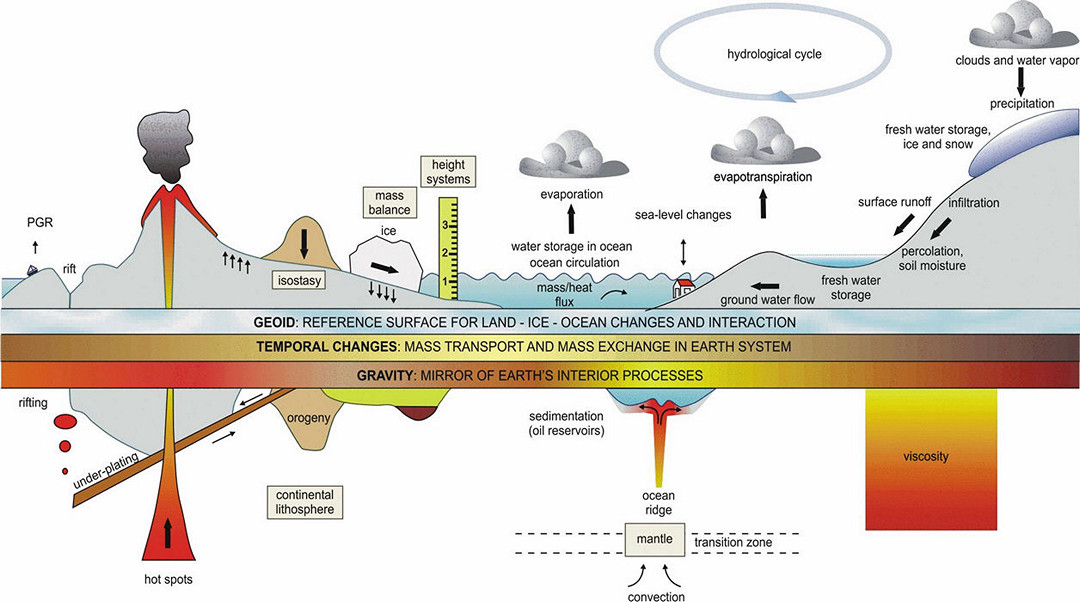
Obrázek 134:
Znázornění vzájemných vtahů a souvislostí – ovlivňujících gravitační pole Země.
(zdroj: GGOS)
Na Zemi umíme skvěle využít sílu lidského intelektu! Super-přesně určujeme trajektorii měřicích satelitů na orbitě Země a „poruchy“ jejich drah nám pomohly získat více informací o naší planetě:
I kdyby byla naše planeta navěky zahalena neproniknutelnou atmosférou – pouze na základě poruch orbit těchto satelitů bychom uměli zjistit mnoho informací o podobě a složení planety Země – umíme totiž „skenovat“ gravitační pole Země a následně určit rozložení hmoty. Jde o brilantní výsledek vědeckého myšlení a technologického pokroku.
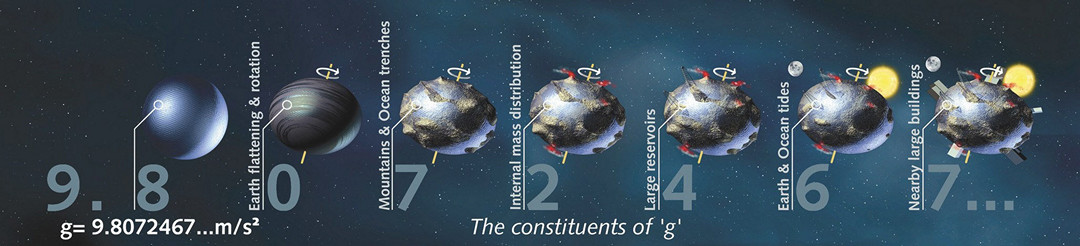
Obrázek 135:
Zjednodušené vyjádření, co vše determinuje hodnotu gravitačního zrychlení na povrchu Země.
(zdroj: ESA-AOES Medialab)
V případě Slunce však lidský intelekt selhává a zcela stejný fenomén (poruchy orbit satelitů obíhajících centrální těleso) neumíme použít stejným způsobem – neumíme naměřené poruchy využít tak, abychom se dozvěděli něco nového o skutečném tvaru, rotaci a distribuci hmoty uvnitř Slunce.
Raději v blízkosti Slunce uvěříme v tajuplný mysteriózní jev (zakřivení časoprostoru), kterým si vysvětlíme všechny naměřené rozdíly, a Slunce prohlásíme za zcela homogenní kouli, jejíž gravitační potenciál je všesměrově naprosto rovnoměrný – za dokonalé a statické božstvo, které nehybně trůní v centru naší SS.
Přestože naše vlastní planeta vykazuje velmi podstatné zploštění, tvarové anomálie, hmotnostní nehomogenity – přestože totéž nacházíme u všech planet Sluneční soustavy – přestože ještě mnohem větší a závažnější deformace deklarujeme u mnoha pozorovaných hvězd – naši vlastní centrální hvězdu postulujeme za dokonale kulovou, zcela homogenní a nehybnou …
… a naměřené poruchy orbit „objasňujeme“ teorií zakřiveného časoprostoru (OTR), či dokonce i v naší SS postulujeme ložiska Temné hmoty (nedávno se objevila „nevysvětlitelná“ precese i u Saturnu).
Vědecké poznání gravitace tak zůstává nadále schizofrenní – fenomenální úspěchy na jedné straně a fatální selhání na straně druhé!
Abychom i nadále vykazovali progres v poznání blízkého i vzdáleného vesmíru, musí se věda rozhodnout, zda bude spíše vědou, anebo spíše náboženstvím – hájícím zbožňovanou Teorii relativity a posvátný heliocentrický model (dokonalá nehybná koule v centru veškerého pohybu).
Vzhledem ke složitosti mechaniky naší SS jde samozřejmě o mezioborový multidisciplinární problém, v jehož centru budou numerické (počítačové) modely všech hmotnostně významných objektů v blízkém vesmíru a Newtonova gravitace v rámci Zákona symetrického pohybu se započtením faktů, že událost (čas) se šíří v rámci pravoúhlého 4D prostoru!
Nic víc není třeba!
Obecná rovnice pohybu lokálně izolované skupiny objektů:


Přičemž vektor rychlosti každého objektu je definován souhrnem gravitačního potenciálu (respektive rozdílem potenciálu) indukovaným všemi ostatními objekty, respektive výsledným časoprostorovým úhlem:
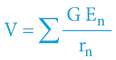
exsec α i = ∆V
ve i = sin αi
C hmotný střed skupiny objektů (barycentrum)
Ei; Enenergie (hmotnost) objektu
sivektor polohy (i-tého) objektu vůči C (délková vzdálenost objektu od hmotného středu)
ve ivektor rychlosti vůči C (měřeno externě z pozice hmotného středu)
pivektor hybnosti vůči C (měřeno externě z pozice hmotného středu)
Vsouhrnný gravitační potenciál
Ggravitační konstanta
rnvzdálenost sledovaného objektu od jiného (n-tého) objektu
Zadáme-li do výkonných počítačů data všech významných objektů v naší SS a numericky budeme řešit výšeuvedené rovnice – výsledkem bude korektní model pohybu nebeských objektů v naší SS (včetně Slunce!) vůči společnému barycentru (C).
Nebude třeba ani zakřiveného časoprostoru, ani Temné hmoty!

