3.4.4 GEOMETRIE ČASOPROSTORU
3.4.4.1 STARÁ ÚLOHA V NOVÉM KABÁTĚ
Vraťme se nyní k osvědčenému příkladu, ale tentokrát již s využitím nově dohodnuté terminologie. Sekundy, minuty a hodiny použijme nejen k vyjdáření časů, ale i k vyjádření délkové vzdálenosti:
Z planety A na planetu B, vzdálených od sebe 2 hodiny, vyletí raketa v čase 00:00:00, rychlostí ve = 1/3. Čas se šíří kolmo k dráze pohybu rychlostí ce = 1. Zakresleme takovou situaci a vypočtěme cílový čas:
Jde o první případ úlohy zadané novou terminologií, takže pro jistotu uvádíme i zadání se „starými“ jednotkami (v závorkách):
Z planety A na planetu B, vzdálených od sebe 2 hodiny (2 160 000 000 km), vyletí raketa v čase 00:00:00, rychlostí ve = 1/3 (100 000 km/s). Čas se šíří kolmo na dráhu pohybu (4. prostorem) rychlostí ce = 1 (300 000 km/s). Zakresleme takovou situaci a vypočtěme cílový čas:
V tuto chvíli si pouze povšimněme, že údaj o rychlosti je bezrozměrný, respektive bez jednotek. Měříme-li vzdálenost v sekundách – jednotky nejsou třeba
sekunda / sekunda = 1.
Věnujme se grafickému vyjádření „staré situace“ novým pohledem:
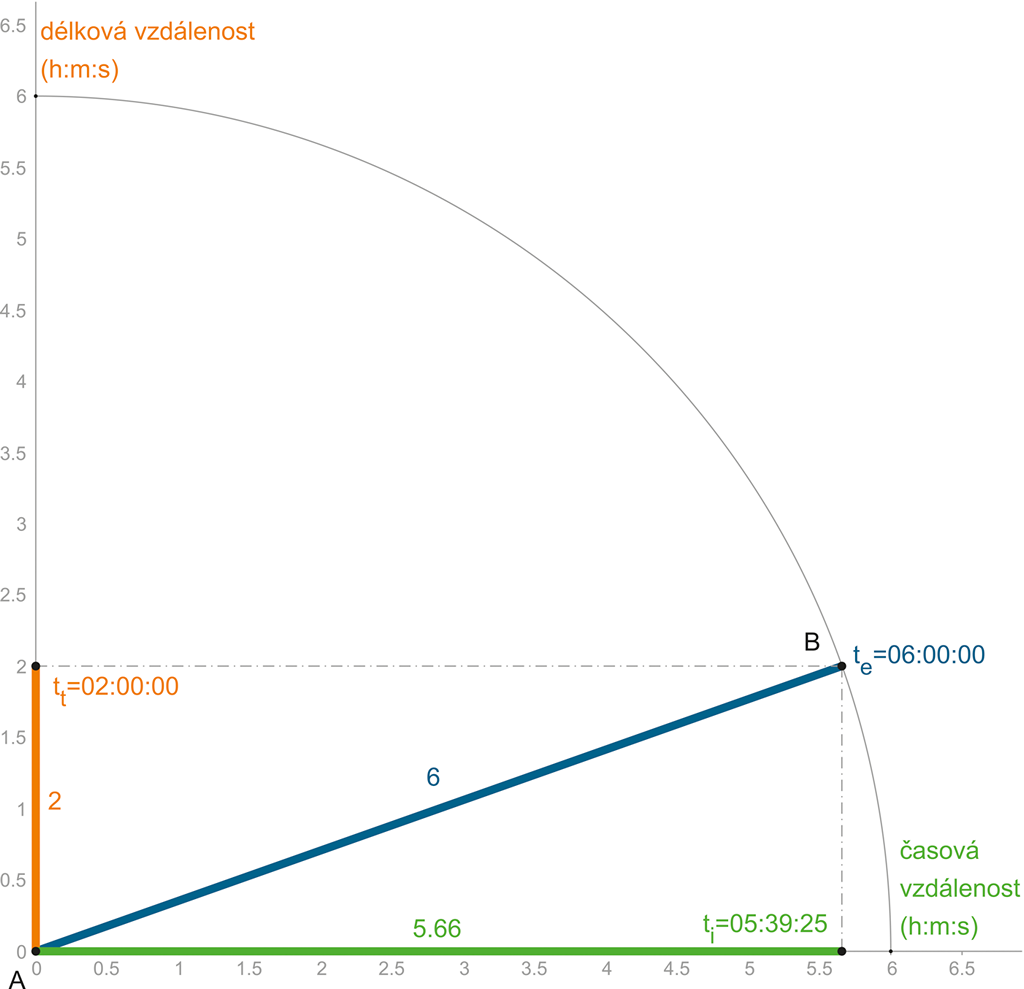
Situace je nyní o mnoho jednodušší a názornější:
Zatímco se kosmická loď přemístila v čase (z pohledu externího pozorovatele) do časové vzdálenosti 6 hodin (te), v délkové vzdálenosti se přesunula pouze do vzdálenosti odpovídající 2 hodinám (tt) – délková vzdálenost odpovídá době (trvání), za kterou cílovou vzdálenost urazí „světlo“, respektive čas.
Takový časoprostorový trojúhelník má jen jedno řešení. Matematický výpočet je snadný (Pythagorova věta):
![]() = cca 5,66 hodiny = cílový čas 05:39:25
= cca 5,66 hodiny = cílový čas 05:39:25
Zatímco z pohledu externího pozorovatele trval celý děj 6 hodin, let byl z pohledu posádky (interního pozorovatele) o 20 minut a 35 vteřin kratší, tedy téměř o 6 %!
Vyjádřeme obecný vztah pro transformaci časů:
![]()
tičas děje měřený interním účastníkem děje
tečas děje měřený externím pozorovatelem děje
verychlost pohybujícího se objektu, z pohledu externího pozorovatele
Čas z pohledu interního účastníka je vůči času externího pozorovatele zkrácen koeficientem „k“:

Důvodem tohoto jevu (bez obav jej nazveme kontrakcí času – jde o dilataci času z perspektivy recipročního pozorovatele) není nic magického ani tajemného. Jde o základní zákony geometrie (Euklidovské geometrie) a bazální matematiky. Je-li čas čtvrtým rozměrem našeho světa – úloha v takovém případě nemůže mít jiné řešení!
Analogické situace běžně nacházíme v našem světě, i když se nepohybujeme „vesmírnými“ rychlostmi:
Budeme-li mít dva plavce v řece, jejíž proud teče rychlostí 9 km/h, a první plavec se nechá nehybně unášet proudem, zatímco druhý popluje kolmo vůči proudu rychlostí 3 km/h – budeme řešit analogickou úlohu, pouze s tím rozdílem, že nejde o řeku času. Geometrie a matematika pravoúhlého trojúhelníka bude totožná!
V každém okamžiku takové situace bude mít za sebou druhý plavec o 6 % větší vzdálenost nežli ten první. A bude-li cílem experimentu uplavat konkrétní prostorovou vzdálenost, ten druhý plavec ji urazí v čase o 6 % kratším!
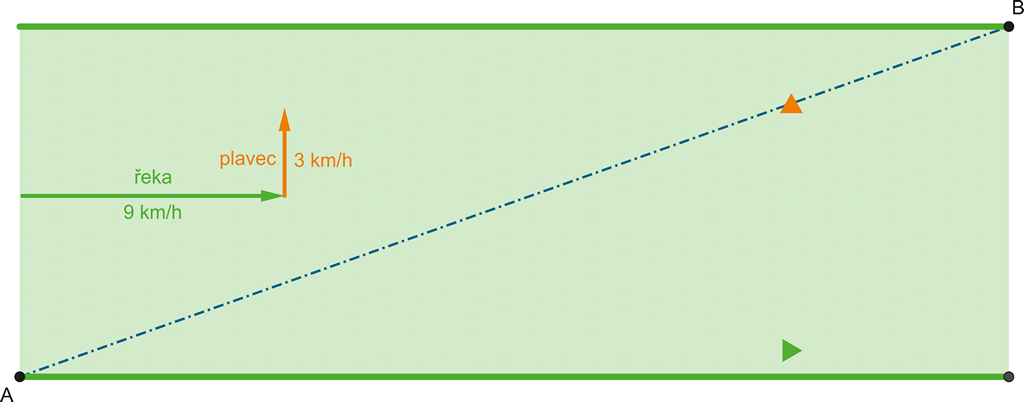
Obrázek 95 + ANIMACE:
Kolmo plující plavec je trvale o 6 % vzdálenější a rychlejší!
ANO – lze cestovat v čase! A také všichni v čase cestujeme:
My všichni (celé lidstvo, včetně kosmonautů v nejrychlejších strojích, co kdy lidstvo sestrojilo) jsme unášeni řekou času. Jsme v situaci onoho prvního plavce, který je pasivně unášen. I ti nejrychlejší z nás jsou vůči rychlosti toku řeky času de facto nehybní – jsme příliš pomalí – lidé dosud nikdy „na vlastní kůži“ nezaznamenali významné „časové disproporce“. Náš časoprostorový trojúhelník je natolik „úzký“, že běžnými chronometry nemůžeme naměřit žádné rozdíly. Budeme muset vynalézt rychlejší dopravní prostředky, abychom jednou mohli alespoň částečně (pouze jednosměrně) vyzrát nad časem a „cestovat“ do budoucnosti.
Vědecké experimenty v částicové fyzice však umožnily lidstvu alespoň nepřímo (externě) sledovat objekty, jejichž rychlost se s rychlostí řeky času již může měřit. V těchto vědeckých experimentech již jsou časové disproporce zcela evidentní – a odpovídají výšeuvedené geometrii, odpovídají Pythagorově větě.
Přesné atomové chronometry dnes dokonce dilataci času prokazují i v laboratorních podmínkách pro objekty běžného makrosvěta a pro běžné rychlosti.
Experimenty prokazují naprosto spolehlivě, že „hypotetická úloha pro základní školy“ (z předchozích kapitol) není v případě času použitelná – čas se nešíří žádným z běžných rozměrů našeho 3D světa – čas má svůj „vlastní“ rozměr a je reálným čtvrtým rozměrem časoprostoru, který lze (nejlépe) povšechně poměřovat a vyjadřovat v sekundách!
Čtvrtá (časová) rovina je vždy kolmá ke všem (tradičním) třem známým rovinám – a tomu odpovídá i související matematika, respektive Pythagorova věta, respektive trigonometrie.
Mnohé napoví následující obrázek:
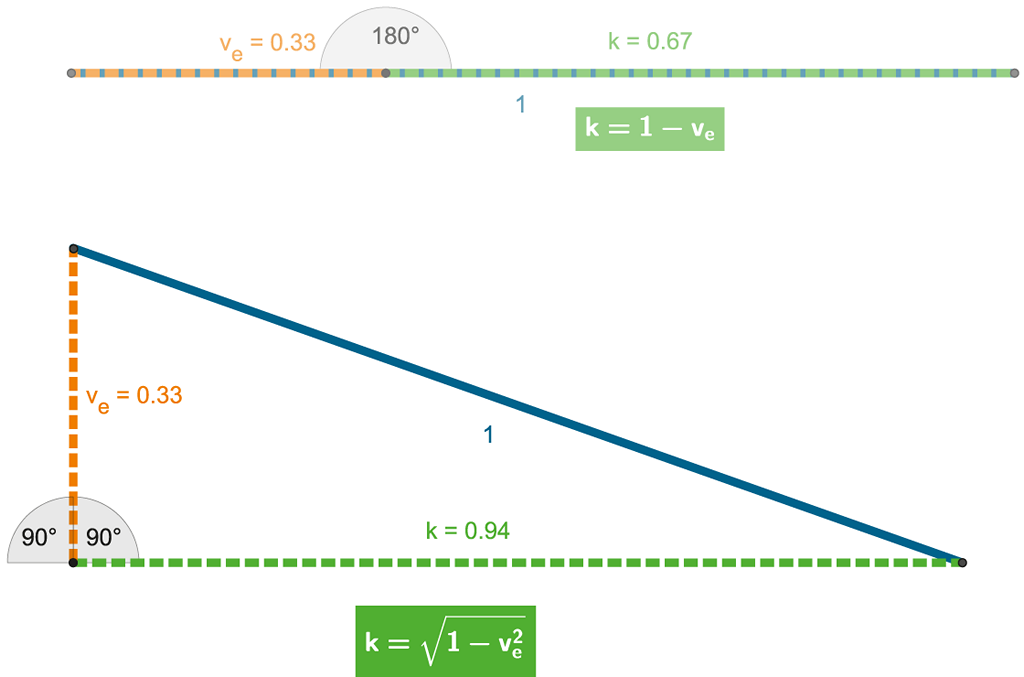
Obrázek 96 + ANIMACE:
Čas se „vyklonil“ z našeho 3D prostoru v pravém úhlu a tomu odpovídá i matematika 4D prostoru.
Věnujme se však hlouběji vlastnostem časosprostoru:
Byť pro primární myšlenku TČ vystačíme s matematikou základních škol (Pyhagorova věta), bude přínosné osvěžit si i matematiku střední školy, respektive trigonometrii – chceme-li spatřit celou „vnitřní krásu“ architektury časoprostoru.

