ROZVOJ TRIGONOMETRIE
Jak již bylo uvedeno výše – o významný rozvoj trigonometrie se zasloužili především indičtí a arabští učenci:
Ve snaze o určení délek pravoúhlého trojúhelníku vepsaného v jednotkové kružnici definovali (cca roku 500) funkce sin a cos.
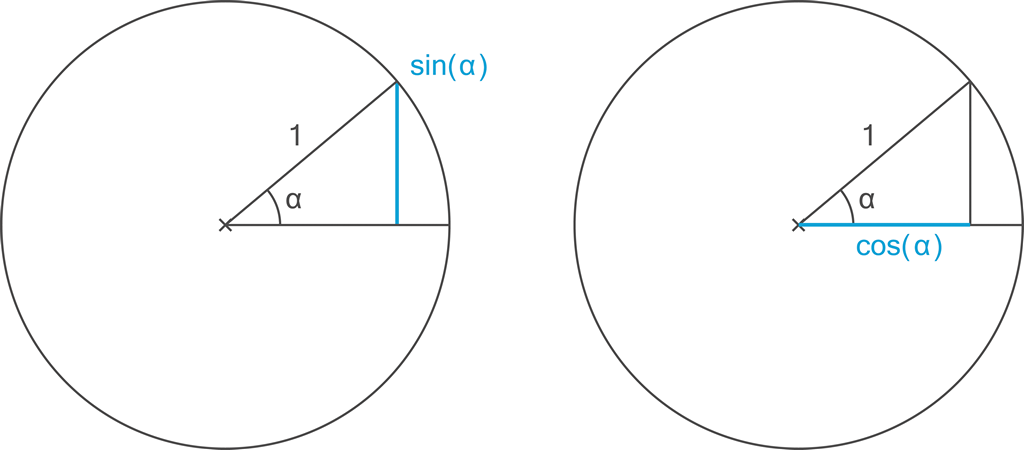
Obrázek 16:
Svět poznal sinus a cosinus.
Dalším jejich zájmem bylo určení délky stínů (i všech ostatních délek) v problematice slunečních hodin (gnómonika). Takto byly odhaleny (cca roku 1000) funkce tan, cotan, sec, cosec:
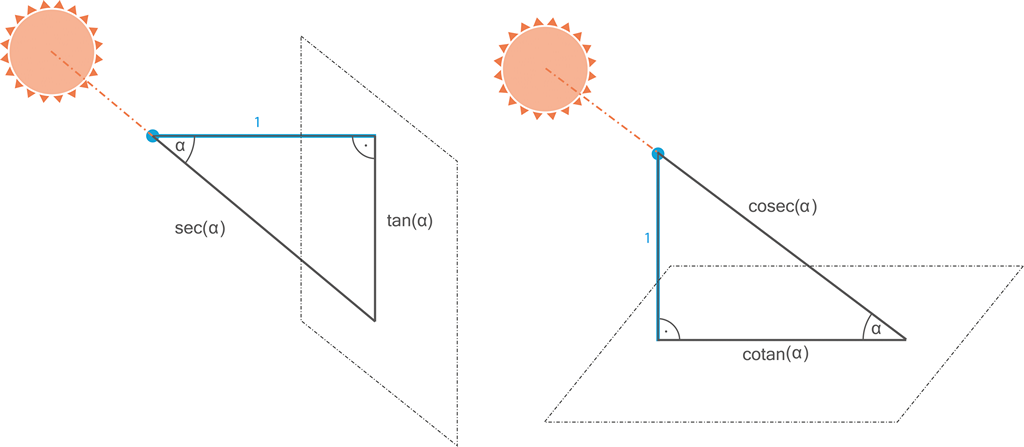
Obrázek 17:
Brzy následovaly funkce tangens, cotangens, secans a cosecans.
Abu l-Wafa (cca 980) již popisuje všechny hlavní trigonometrické funkce jako délky související s kružnicí – tedy dnešní perspektivou!
Al-Birúní (ten, který přesně změřil velikost Země) následně zpracoval tabulky těchto funkcí v jednotkové kružnici. Evropské učence tak předběhl o celá staletí!
Kolem roku 1000 tak dosáhla znalost trigonometrických funkcí asijských učenců de facto absolutoria. Dnešní středoškolská matematika zpravidla neučí studenty o nic víc!
Na tomto místě je proto vhodné si připomenout matematiku jednotkové kružnice:
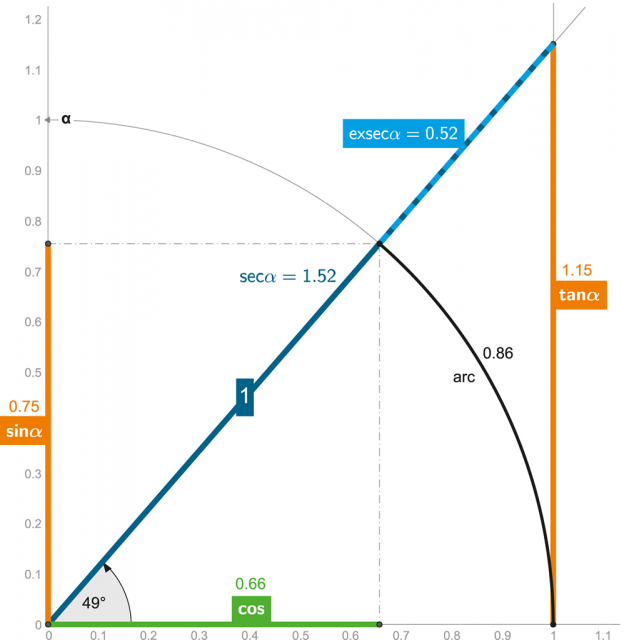
Obrázek 18 + ANIMACE:
Vše důležité v jednotkové kružnici = trigonometrie (klasické zobrazení).
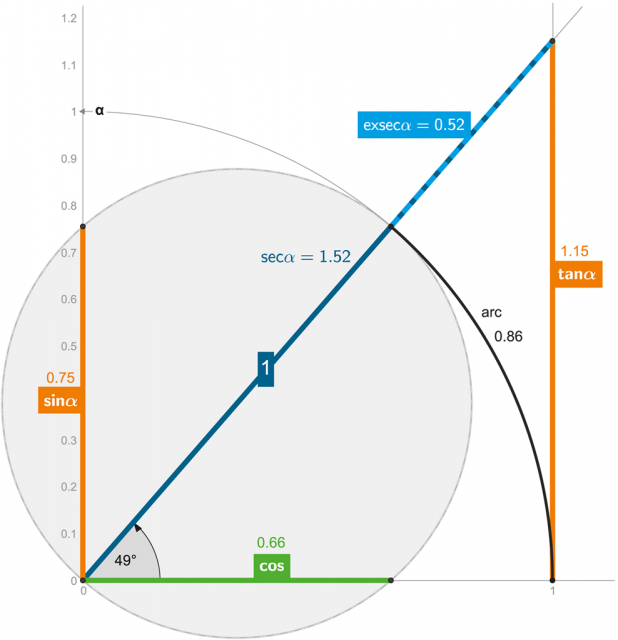
Obrázek 19 + ANIMACE:
Stejná trigonometrie v názornějším „kulatém“ zobrazení.
Obrázek 19 je velmi názorný proto, že trigonometrické funkce lze snadno demonstrovat rotací kružnice (s jednotkovým průměrem) kolem ústředního bodu [0;0]: Na obou osách (x; y) bude průnik takovéto kružnice přímo vytyčovat funkce sinus a cosinus, přičemž osa kružnice nám vytyčí tangentu a délka úsečky na této ose definuje secans.
V obou zobrazeních jsme také vyznačili „historickou“ funkci exsecans (exsec), která není ničím jiným nežli sekantou poníženou o jedničku (poloměr jednotkové kružnice je 1!) – funkce exsecans se nám bude hodit v dalších kapitolách, neb má přímou interpretaci v astronomii i souvisejících vědách.
Také je třeba si objasnit význam pojmu „arcus“ (arc):
Ze školy jsme většinou navyklí vyznačovat úhel ve vnitřním rohu daného trojúhelníku … a učitelé nám často zapomněli objasnit, že primárně hodnota úhlu vyjadřuje délku jednotkového oblouku!
Právě proto fyzikové a matematikové vyjadřují úhly nejraději v (těch podivných) radiánech – kde pravý úhel není 90°, ale π/2 (tedy cca 1,57). Vyjadřujeme-li úhly v radiánech, pak je ve výšeuvedených diagramech vše proporcionálně úměrné – hodnota úhlu (rad) pak přímo vyjadřuje délku obvodu kruhové výseče daným úhlem vytyčené.
A protože „kruhový oblouk“ (část obvodu kružnice) je historicky označován pojmem „arcus“ (arc) – lze pojem „arcus“ interpretovat jako „úhel“:
Ve výsledku si stačí zapamatovat, že úhel vyjadřuje primárně délku oblouku – proto se nelze v geometrii obejít bez radiánů – stejně tak, jako se nelze při výpočtu obvodu kružnice obejít bez magického čísla π – vše spolu velmi úzce souvisí!
Suma sumárum:
Radiány jsou mnohem lepší nežli stupně!
Pravý úhel se rovná π/2, protože obvod kružnice jednotkové délky je roven 2π – čtvrtina kruhu má tudíž délku π/2, šestina kruhu (úhel 60°) má tudíž délku π/3 atd.
Teprve (a pouze) když udáváme hodnotu úhlů v radiánech – nacházíme v trigonometrických funkcích jejich „vnitřní krásu“ a hlubší smysl Euklidovské geometrie.
Byť většina dnešních studentů nedoceňuje význam trigonometrických funkcí – jsou bez nadsázky stěžejní oblastí matematiky i reálného světa.
Klesá-li v zimě teplota (oproti létu) – důvodem je klesající sinus úhlu, pod nímž paprsky Slunce dopadají do naší krajiny. Navzdory rozšířenému omylu je zeměkoule v zimě (paradoxně) blíže Slunci, nikoliv dále – vzájemná vzdálenost je totiž téměř konstantní a nesouvisí s ročními obdobími – teplotu počasí řídí sinus úhlu dopadající sluneční energie.
Budeme-li tlačit nepojízdné vozidlo po silnici – efektivita našeho snažení bude naopak přímoúměrná cosinu úhlu, pod nímž budeme na vozidlo působit silou.
Bez pochopení trigonometrických funkcí bychom nevěděli nic o okolním vesmíru, nefungovaly by mechanické ani elektrické stroje a o rozhlasovém či televizním vysílání bychom si mohli nechat pouze zdát.
Bez trigonometrických funkcí by nikdy nevznikly mapy našeho světa (a vesmíru), námořní lodě by náhodně bloudily po moři – netušíce, jakým směrem mají plout za svým cílem.
Znalost trigonometrických funkcí byla dále rozšířena zejména událostmi:
• Kartograf Gerhard Mercator (1569) poprvé integruje (zatím pouze numericky) trigonometrickou funkci ∫ sec α, když vytváří první mapu světa, která korektně převádí 3D situaci zemského globu do 2D roviny a přitom zachovává vzájemné směry (úhly), zatímco pokřivuje vzdálenosti a tvar kontinentů. Od té doby byla mořeplavba mnohem bezpečnější a námořní navigace o hodně snazší!
• John Napier (1614) objevil logaritmy ve snaze převést součin trigonometrických členů na jejich součet.
• Leibniz (1670) a Newton (1671) definovali základní trigonometrické funkce jako řešení specifických diferenciálních rovnic (například funkce sinus i cosinus jsou řešením rovnice ÿ = –y). Jimi objevený integrální počet navíc umožnil analyticky (přesně) řešit integrály trigonometrických funkcí (třeba Mercatorovu úlohu).
• Leonhard Euler (1748) definoval matematické řady, kterými lze spojitě matematicky vypočítat trigonometrické funkce. Do té doby bylo totiž nutné používat nespojité (více či méně nepřesné) tabulky a chybějící hodnoty nějak přibližně interpolovat.
1.16.1 ZA VŠÍM HLEDEJ TROJÚHELNÍK …
… a občas i ženu !
Kolem roku 1000 (našeho letopočtu) již lidstvo umělo zdárně používat všechny stěžejní trigonometrické funkce a od asijských učenců tyto znalosti přebírala postupně (během několika staletí) i Evropa a zbytek světa. Trigonometrické tabulky zprostředkovávaly tehdejším učencům a „inženýrům“ podobnou službu, jakou dnes poskytují vědecké kalkulačky. Stavitelům, zeměměřičům i astronomům tak již nic nestálo v cestě za poznáním.
Díky ovládnuté matematice trojúhelníku mohlo lidstvo poprvé začít přesně a exaktně „mapovat“ nejen náš svět (zeměkouli), ale i naše místo ve vesmíru a finálně i samotný vesmír. A ať již v této souvislosti narazíme na pojmy trigonometrie, triangulace, trilaterace či paralaxa – vždy jde de facto o totéž – o výpočet všech (zprvu neznámých) parametrů trojúhelníku na základě parametrů známých.
Na výšeuvedeném principu se za uplynulých tisíc let nic nezměnilo – a stejný mechanismus bude dozajista fungovat i za další tisíciletí. V tomto ohledu je, například, způsob práce dnešních zeměměřičů úplně stejný jako v přední Asii roku 1000:
Ideální zeměměřičský tým sestává ze dvou osob a jedné tyče o známé délce. Tyč je vždy „etalonem“ délky, respektive „jednotkovou“ mírou, a proto je lhostejno, zda je tyč „metrová“ či „palcová“ – výsledek měření totiž bude vždy ve shodných jednotkách.
Pro zjednodušení si však v následujícím scénáři představme, že zeměměřiči sebou vláčejí tyč o délce jeden metr.
Většina čtenářů již asi někdy viděla zeměměřiče – způsob práce je zpravidla takovýto scénář (č. 1):
Vrchní zeměměřič stojí na místě s měřicí „trojnožkou“ (s optickým úhloměrem), zatímco podřízený pobíhá s jednotkovou tyčí po terénu, který je třeba přeměřit. Chce-li zeměměřič určit vzdálenost nějakého konkrétního místa v prostoru – pak se v dané lokaci podřízený pracovník s tyčí zastaví, aby vrchní zeměměřič mohl provést své (trigonometrické) měření.
Většinou je praktičtější etalonovou tyč v daném místě vztyčit vertikálně (aby byla lépe vidět) – měření však bude stejně validní a přesné i v situaci, kdy bude tyč ležet horizontálně – z důvodu názornosti bude horizontální scénář použit i v následujících vyobrazeních:
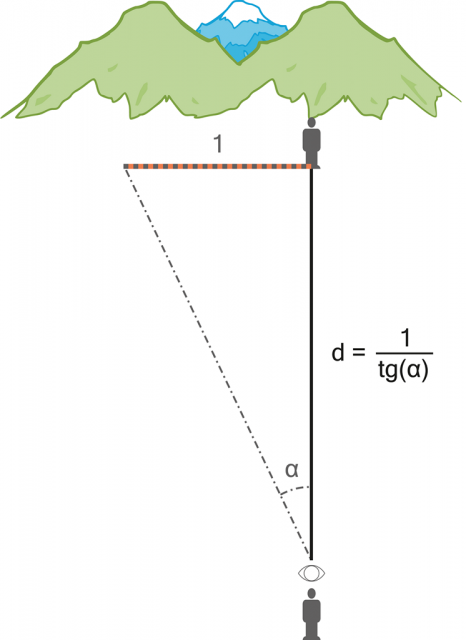
Obrázek 20:
Cílem je změřit úhel, pod nímž se bude jevit metrová (jednotková) tyč.
Jakmile vrchní zeměměřič změří úhel, pod kterým se mu bude jevit „jednotková“ tyč – je již snadné (na základě trigonometrických funkcí) dopočítat vzdálenost, respektive určit kolikrát je měřená vzdálenost delší nežli „jednotkový“ tyčový etalon.
K měření vzdáleností je taktéž možné použít alternativní scénář (č. 2):
Představme si situaci, kdy se (sklerotický) pomocný zeměměřič vydá na určenou „kótu“ a zapomene sebou vzít měřicí tyč … na vzdáleném místě v terénu tím pádem pouze gestikuluje a mává na svého šéfa. Takováto situace je jen zdánlivě nepříznivá a vrchní zeměměřič se nenechá vyvést z míry:
Zkušený profesionál v takové situaci změří úhel (azimut), pod kterým vidí svého podřízeného. Následně vedle sebe položí měřicí tyč a provede druhé měření z „posunutého“ místa, které je od (místa původního) vzdálené o etalonovou „jednotkovou“ délku. Naměří, že jeho kolega se tentokráte jeví pod poněkud jiným úhlem (azimutem). Tento úhlový posun je opět hledaným úhlem (α)!
Vzdálenost lze následně opět určit snadno – dle výšeuvedeného vztahu.
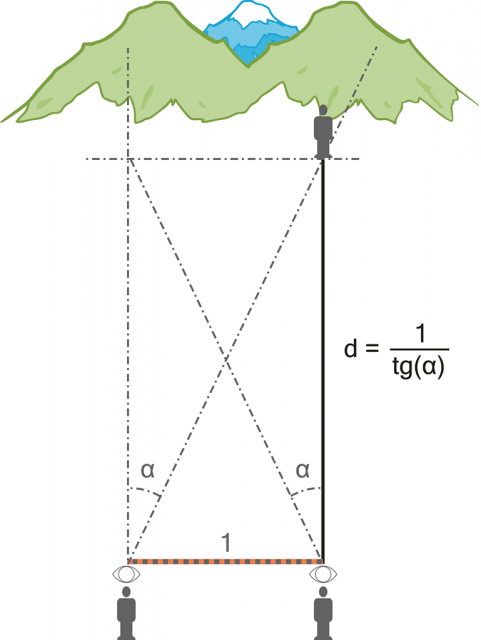
Obrázek 21:
Oba měřicí scénáře měří shodný úhel!
Pozorný čtenář již možná pochopil, že druhý zeměměřičský scénář je typickým určením tzv. „paralaxy“ – na stejném principu (mimochodem) určuje vzdálenost předmětů i náš mozek, porovnáním obrazu levého a pravého oka.
První a druhý scénář mají mnoho společného, a přesto jsou tyto scénáře rozdílné:
Společným jmenovatelem je trigonometrie – Euklidem položené základy obohacené o trigonometrické funkce (sin, cos, tan, …) umožňují spočítat všechny parametry „hledaného“ trojúhelníku, a tím přesně určit vzdálenosti a rozměry v našem světě. Ať již postupujeme první či druhou metodou – vždy je výsledkem shodný trojúhelník, a tedy i shodné výsledky!
Druhý scénář má však tu výhodu, že do cíle měření nemusíme nikoho posílat s jednotkovou tyčí ani jakýmkoliv jiným měřidlem – stačí přemístit měřicí aparaturu o konkrétní délku a na základě pozorovaného úhlového posunu umíme exaktně určit vzdálenost jakéhokoliv předmětu!
Druhý scénář (měření paralaxy) je tudíž nepostradatelný například v astronomii. Na druhé nám nejbližší hvězdě (Proxima Centauri) nemusel nikdo nikdy stát s měřicí tyčí.
Protože se Země během roku pohybuje na své orbitě kolem Slunce (a díky jiným trigonometrickým měřením známe rozměry této orbity), umíme změřit paralaxu (úhlový posun) této hvězdy ze dvou „krajních“ poloh zemské orbity … a následně je již triviální určit vzdálenost Proximy Centauri (cca 4·1016 metrů ≈ 4,2 světelného roku) – opět jde „jen“ o výpočet tangenty!
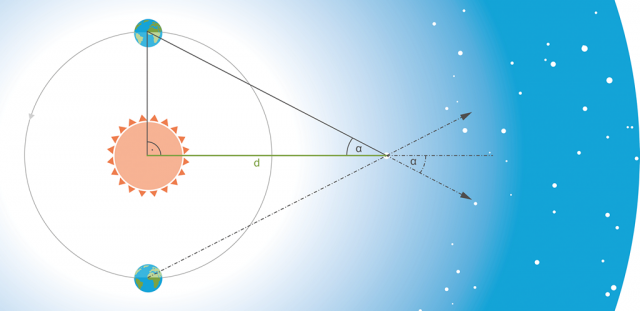
Obrázek 22:
Tisíc let starý princip nám pomáhá měřit vesmír.
Co dodat?
Trigonometrie je základem téměř veškerého našeho vědění!
Díky matematice trojúhelníku umíme změřit rozměry pozemku, vzdálenost kontinentu i vzdálenost nebeského tělesa, … a když radary zjišťují polohu letadla, když navádíme kosmickou sondu, když navigace v mobilním telefonu určuje vaši polohu – vždy je nejhlubším základem všeho trojúhelník a základní trigonometrické funkce!
Za vším hledej trojúhelník!

