3.4.9 RESUMÉ K ZÁKONU 4D PROSTORU
Z4DP:
Vše existuje v Euklidovském čtyřrozměrném prostoru, který je tvořen třemi délkovými rozměry a jedním rozměrem časovým.
Zákon 4D prostoru (Z4DP) vyjadřuje geometrii světa, v němž reálně žijeme, respektive geometrii časoprostoru.
Jde o synergické spojení obou kategorií – času (kauzální pořadí a trvání dějů) a prostoru (poloha a trajektorie dějů) – v kategorii jedinou. Jde o evoluci myšlenek Minkowského 4D prostoru.
Pochopíme-li myšlenkovou konstrukci Z4DP, pomůže nám to mnohem lépe uchopit fyzikální kategorii „čas“:
Samotná existence 4D prostoru – kde čas je čtvrtým (kolmým) rozměrem ke třem rozměrům délkovým – je soběstačným vysvětlením „mezní“ rychlosti „světla“ i prokázaných fenoménů souvisejících s dilatací času. Nic víc není třeba!
Nemusíme nic dalšího postulovat – a časoprostorová kružnice (respektive pravoúhlý trojúhelník v této kružnici) dají odpovědi na všechny „podivné“ jevy, které zaznamenala fyzika v posledních dvou stoletích.
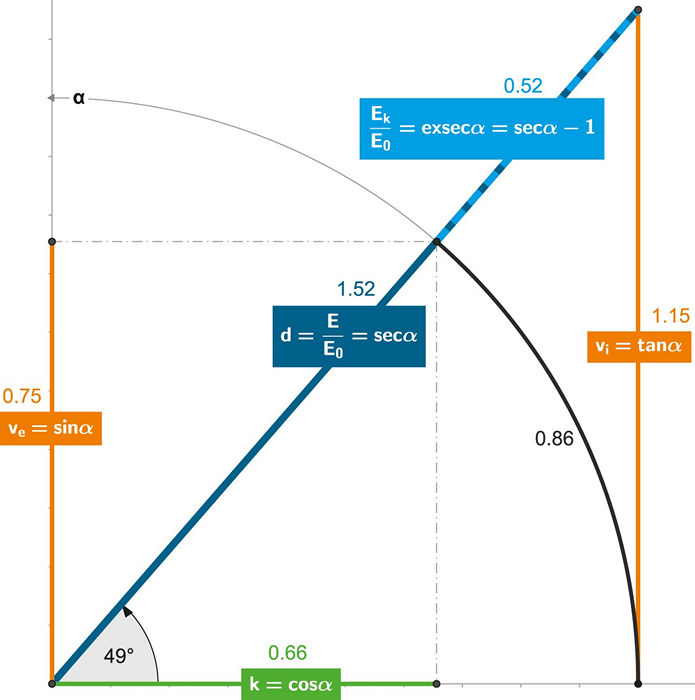
Obrázek 115:
Klíčem k pochopení 4D časoprostoru je matematika jednotkové kružnice.
Z oné jednoduché geometrie plyne vše:
Objasňuje, proč jsme dosud (v roli externích pozorovatelů) vždy zaznamenali jistou „mezní“ rychlost šíření hmoty (a šíření informace). Objasňuje, že tento jev je přímým důsledkem existence 4D časoprostoru. Ona mezní „rychlost světla“ není faktickým fyzikálním omezením – je zdánlivým projevem skutečnosti, že čas je 4. rozměrem našeho světa – je důsledkem 4D časoprostoru.
externí rychlostve = sin α
Rychlost pohybu hmoty není nikterak omezená! To, že vnímáme rychlost šíření světla jako omezenou, je důsledkem geometrie časoprostoru – optikou externího pozorovatele (který se neúčastní samotného pohybu). Existence času ve 4D časoprostoru se externímu pozorovateli projevuje zdánlivou omezeností rychlosti pohybu. Pro samotný pohybující se objekt (optikou interního pozorovatele) však rychlost pohybu není jakkoliv omezena.
interní rychlostvi = tan α
Z4DP nás přiblížil pochopení času, byť ne zcela:
I navzdory TČ nevíme o čase zdaleka vše – je příliš imaginární kategorií. Nicméně – naše finální stanovisko vyvozuje, že „čas“ ve skutečnosti „zapisuje“ pořadí změn (délkové) polohy objektů v prostoru. Hodinami měříme pořadí změn, které se v prostoru dějí – rozeznáváme tímto mechanismem kauzalitu, tedy příčinu a následek – a říkáme tomu čas!
Délkovou i časovou vzdálenost vzájemné polohy objektů v časoprostoru měříme stejnou prostorovou jednotkou! V rámci TČ je touto jednotkou sekunda. Vzdálenost ze Země na Měsíc je tedy cca 1,25 sekundy.
Ať již se pohybujeme, anebo naopak tvrdíme, že jsme v klidu – vždy se pohybujeme prostorem (časoprostorem)! Rozdíl je vždy jen v mixu toho, z čeho každá sekunda našeho bytí sestává. Jsme-li v klidu, je celá naše sekunda tvořena pouze sekundou časovou – pohybujeme-li se, jde o mix sekundy časové a délkové takovým způsobem, že jejich „pythagorský“ součet je vždy roven jedné. Dosáhneme-li „rychlosti světla“, zůstává již pouze délková sekunda a její časová část je nulová – respektive rychlost pohybu je nekonečná a za sebemenší časový okamžik lze procestovat třeba celý vesmír (interní optikou).
Externí optikou je rychlost světla (času) 1! Tak to vždy bylo, je a bude – v celém vesmíru. Je to ona magická, úžasná a veledůležitá jednička (c=1)!
Matematika pravoúhlého trojúhelníku (jednotkové kružnice) je velmi jednoduchá a lidstvu známá již po tisíciletí. Stačí si ji jen připomenout – nic víc není třeba. Není třeba kontrakce délek – není třeba, aby se vesmír zkracoval ve směru pohybu pro každý vesmírný objekt – není třeba, aby metrová tyč při pohybu zkracovala svoji délku. Vzdálenost ze Země na Měsíc může zůstat na hodnotě 1,25 sekundy pro každého.
Matematika 4D časoprostoru způsobuje proměnný „tok“ času, respektive rozdílné vnímání rychlostí. Délky však zůstávají pro každého stejné!
Dilataci času spoluprovází kontrakce času! Záleží na tom, kdo činí ono časové porovnání. Interní účastník děje zaznamenává (v důsledku existence 4D časoprostoru) kontrakci svého času vůči externímu času, externí pozorovatel naměří naopak dilataci svého času vůči internímu času. Spolu s tím zaznamená interní účastník vyšší rychlost (teoreticky principálně neomezenou), zatímco externí účastník naměří zpomalování rychlosti, jež se limitně bude blížit „rychlosti času“ (c=1).
kontrakce časuk = ti/te = cos α
dilatace časud = te/ti = sec α
Stejná matematika i objasňuje výpočet kinetické energie, respektive celkové energie, respektive objasňuje ono známé E = m c2 (jež jsme si v rámci TČ zjednodušili na E = m).
nárůst celkové energieE/E0 = sec α = d
poměr kinetické energieEk/E0 = exsec α = sec α –1
V neposlední řadě nám tato jednoduchá matematika (na základě jednoduché geometrie) dala odpovědi na naléhavé otázky cestování ke hvězdám – fantaskní předpovědi TR bylo třeba zreálnit.
Externí čas rovnoměrně zrychleného pohybu
 ; kde vi = a ti
; kde vi = a ti
Především však Z4DP jednou provždy odmítl „princip relativity“:
Pohyb není relativní – časové posuny nejsou relativní – rozdíly v rychlostech ani přírůstky hmotností v důsledku kinetické energie nejsou relativní:
Ten, kdo naměří větší rychlost …
ten, komu plyne pomaleji čas …
ten, kdo musí platit větší „účet za energii“ …
… je tím, kdo má objektivně více pohybu!
A jaké je tedy ono objektivní místo v prostoru, vůči němuž se pohyb odehrává?
Odpoví následující zákon:

