3.5.5 PROSTOROVÁ KRUŽNICE DVOU OBJEKTŮ
I v případě dvou (a více) objektů zůstává v platnosti Zákon 4D prostoru – časoprostorová kružnice se vztahuje na všechny objekty, které se účastní daného pohybového děje. Pro jednoduchost si představme dva objekty jediného pohybového děje a všechny konsekvence:
Newton kdysi demonstroval svoji myšlenku gravitace na příkladu „supervýkonného“ děla (střílejícího horizontálně své projektily až na oběžnou dráhu Země). Proč si od velikána fyziky nevypůjčit takovýto scénář? Pojďme jej mírně modifikovat:
Představme si „speciální“ dělo – které má dvě hlavně, proti sobě postavené, a jednu společnou „spalovací komoru“ s náloží obrovské „čisté“ energie a dva projektily v obou hlavních. Pro názornost celého scénáře předpokládejme i několik zjednodušujících podmínek, jež jsou pouze technologickým (nikoliv principiálním) problémem:
• Dělo je umístěno v hlubokém vesmíru mimo dosah gravitačních polí (vše splňuje podmínku lokálně izolovaných objektů).
• Dělo je vyrobené z ultralehkých materiálů a jeho hmotnost je zanedbatelná v porovnání s hmotnostmi projektilů a nálože (výpočty budou názornější a jednodušší).
• Součástí děla bude i měřicí aparatura, která po výstřelu zprostředkuje měření celého pohybového děje – optikou externího pozorovatele (v barycentru „C“).
• Součástí každého projektilu bude taktéž měřicí aparatura, která po výstřelu zprostředkuje měření celého pohybového děje – optikou obou interních pozorovatelů.
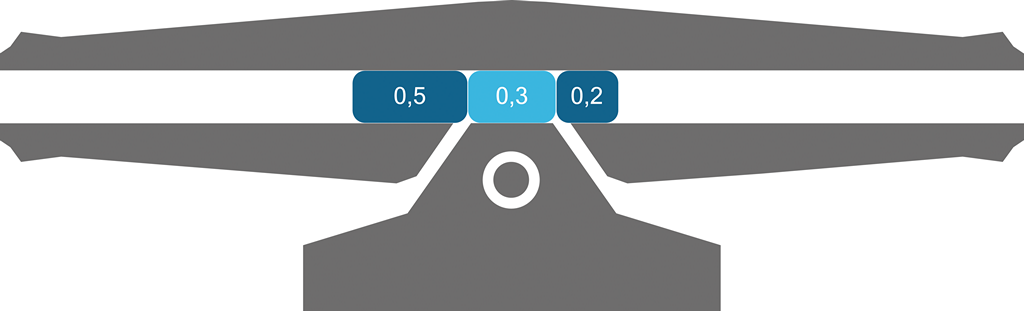
Obrázek 118:
Idealizované, dvouhlavňové dělo s čistou energií ve spalovací komoře.
Nechť:
• Projektil (A) má primární energii (klidovou hmotnost) E0a = 0,2 kg.
• Projektil (B) má primární energii (klidovou hmotnost) E0b = 0,5 kg.
• Nálož je ve formě „čisté energie“ (anihilace hmoty a antihmoty), která uvolní kinetickou energii Ek = 0,3 kg (2,7·1016 J).
Na počátku experimentu tak máme v hlubokém vesmíru lokálně izolovanou skupinu objektů o celkové energii E∑ = 1 kg (9·1016 J).
Počáteční polohu děla v prostoru označme polohou C (centrum = barycentrum).
Znajíce skutečnost, že energie je ekvivalentem hmotnosti, nebudeme se v rámci tohoto scénáře již nadále zabývat přepočtem kilogramů na energii a budeme v textu vyjadřovat i energii v kilogramech (komu to nebude vyhovovat, nechť si náš údaj vynásobí hodnotou 9·1016).
Opět budeme rychlost (v) uvádět jednotkovou (podílem k rychlosti světla, respektive času), stejně tak dráhu (prostorovou délku) budeme vyjadřovat v sekundách, jak jsme již definovali u jednotkové kružnice v předchozích kapitolách – všechna čísla tak budou přehlednější.
Rychlost projektilu A budeme vyjadřovat jako v a časoprostorový úhel jako α.
Rychlost projektilu B budeme vyjadřovat jako w a časoprostorový úhel jako β, alternativně budeme rychlost označovat obecně se dvěma indexy (příklad: vab ≈ objekt A měří rychlost objektu B).
3.5.6 SITUACE PŘED VÝSTŘELEM
Před výstřelem jde o situaci „klidu“ – žádná hmota se vůči lokálnímu hmotnému středu nepohybuje – časoprostorový úhel pohybu obou objektů je nulový, všechny rychlosti jsou nulové a hybnosti jsou taktéž nulové.
α = 0; β = 0
vca = ve = 0; vac = vi = 0
wca = we = 0; wac = wi = 0
E0a = 0,2 kg; E0b = 0,5 kg; Ek = 0,3 kg; E = E∑ = 1 kg
p = 0 kg
Obrázek 119:
Před výstřelem jsou všechny dynamické parametry nulové.
3.5.7 SITUACE PO VÝSTŘELU
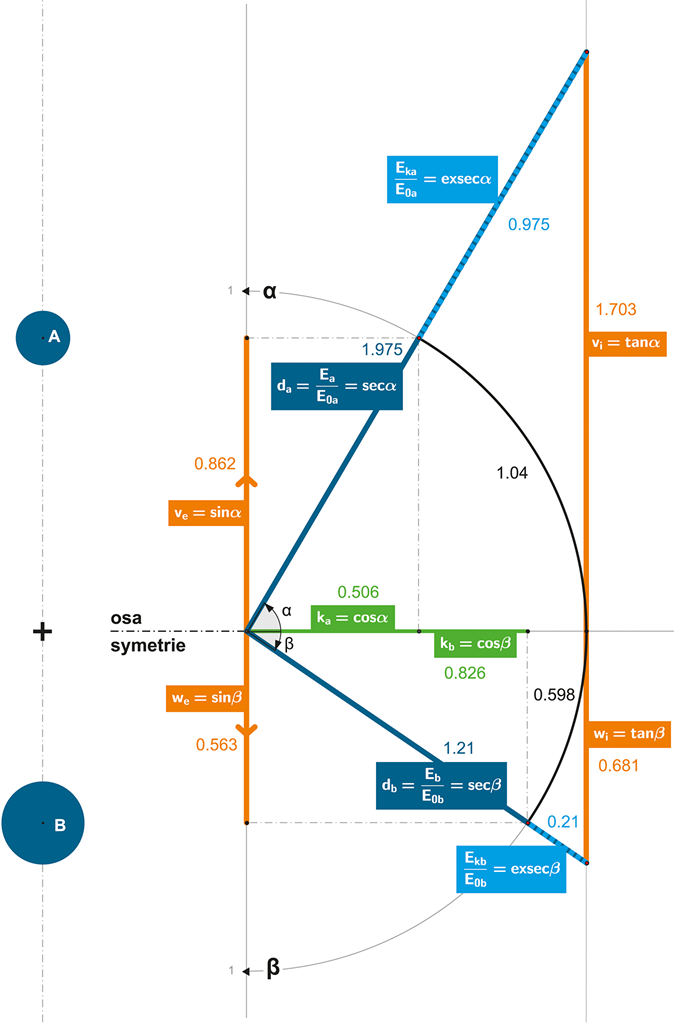
Obrázek 120 + ANIMACE:
Situace po výstřelu.
Situace po výstřelu musí vyhovovat Zákonu symetrického pohybu (a samozřejmě i Zákonu zachování energie/hmoty). Rozložení hmoty v prostoru po výstřelu musí být neustále délkově symetrické, respektive „vyvážené“ – vůči hmotnému středu (bod C), který je fakticky oním objektivním a primárním místem prostoru, vůči němuž pohybový děj probíhá.
3.5.7.1 ENERGETICKÁ SITUACE
Zde samozřejmě platí obecné vztahy jednotkové kružnice a celková energie těles roste spolu s funkcí secans úhlu, respektive dle (nám již známé) matematiky z předchozích kapitol:
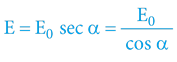
Energie nálože v hlavni (0,3 kg) se po výstřelu proměnila v čistou kinetickou energii, která se rozdělila mezi oba objekty takovým způsobem, aby celkový součet energie soustavy zůstal zachován a aby přitom oba objekty byly neustále hmotnostně symetricky rozmístěny v prostoru (vůči svému hmotnému středu „C“).
Odvozením vzorců nebudeme čtenáře obtěžovat – výsledkem jsou vztahy:
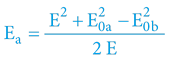
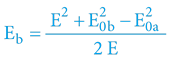
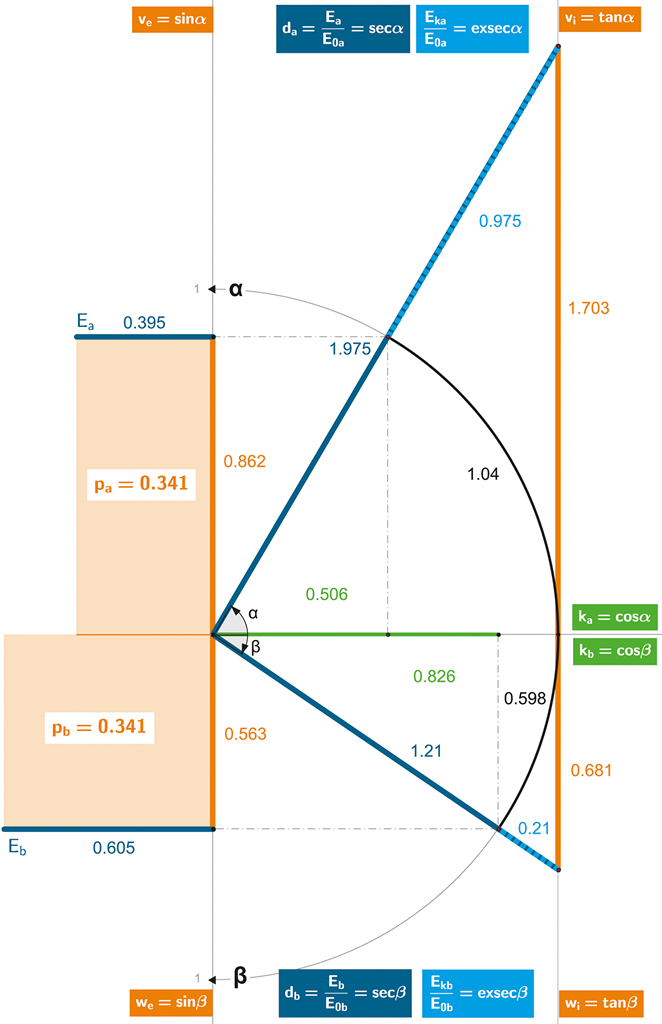
Tyto matematické vztahy generují pro náš vzorový příklad hodnoty:
Ea = 0,395 kg
Eb = 0,605 kg
E = E∑ = 1 kg
3.5.7.2 POHYB TĚLESA A
Známe-li na základě předchozí kapitoly nárůst celkové energie obou objektů (A, B), známe tak de facto časoprostorový úhel, protože:
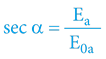; tedy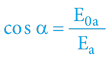 
Dopočtení všeho zbývajícího je již snadné (dle vzorců jednotkové kružnice):
vca = ve = sin α
vac = vi = tan α
Výšeuvedené vztahy generují pro náš vzorový příklad hodnoty:
α = 1,04 rad (59,58°)
vca = ve = 0,862
vac = vi = 1,703
3.5.7.3 POHYB TĚLESA B
Dopočíst rychlosti objektu B je analogicky stejně snadné:
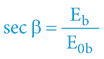; tedy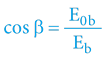 
Dopočtení všeho zbývajícího je již snadné (dle vzorců jednotkové kružnice):
vcb = we = sin β
vbc = wi = tan β
Výšeuvedené vztahy generují pro náš vzorový příklad hodnoty:
β = 0,598 rad (34,265°)
wcb = we = 0,563
wbc = wi = 0,681
3.5.7.4 OBECNĚ
Budeme-li danou situaci kalkulovat perspektivou jednoho (ze dvou) účastníků pohybového děje, bude obecně platit nížeuvedená matematika:
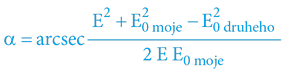
3.5.7.5 HYBNOST
Skutečnost hmotnostně-symetrického rozmístění hmoty v prostoru zajišťuje shodný součin rychlosti a energie (hmotnosti) na obou stranách – v každém okamžiku (před i po výstřelu z děla) tak bude situace energeticky (hmotnostně) „vyvážená“ – na pomyslných vahách vždy dosáhneme rovnovážného stavu:
Vynásobíme-li délku ramene „váhy“ energií (hmotností) tělesa – výsledek bude na obou stranách vždy tentýž!
Na našem grafu se tento fakt projeví skutečností, že virtuální „plocha“ obdélníku hybnosti E · v je u obou těles totožná – sumární hybnost celé soustavy těles zůstává tudíž nulová (jako před výstřelem):
Obrázek 121:
Pomyslná „váha“ hybnosti (plocha) musí být vždy vyvážená.
Ve fyzikální terminologii je výše popsaný stav důsledkem Zákona zachování hybnosti:
p = 0,341‒0,341 = 0 kg
Protože se obě tělesa pohybují opačným směrem – celková hybnost soustavy zůstává po výstřelu neměnná, respektive nulová – důsledek Zákona symetrického pohybu.
3.5.7.6 REKAPITULACE
Měřicí přístroje v barycentru (C) zůstanou po výstřelu na svém původním místě v prostoru, nebudou se účastnit pohybového děje a zůstává jim pouze role externího pozorovatele (a role hmotného středu soustavy objektů). Z této pozice naměří přístroje méně hmotnému objektu A rychlost 0,862 a hmotnějšímu objektu B rychlost 0,563.
Samotné pohybující se objekty však vlivem kontrakce času (dle prostorové kružnice) naměří samy sobě rychlosti vyšší – objekt A si naměří rychlost 1,703 (tedy 1,975násobek) a objekt B si naměří rychlost 0,681 (tedy 1,21násobek).
I po výstřelu funguje energetická bilance:
Původních 0,3 kg čisté energie uvolněné při výstřelu se rozdělilo mezi oba objekty tak, že objekt A získal 0,195 kg 0,2 · 0,975 = 0,195 kinetické energie a hmotnější objekt B získal „jen“ 0,105 kg 0,5 · 0,21 = 0,105 kinetické energie.
Celková souhrnná energie (hmota) celé soustavy je i po výstřelu rovna 1 kg!
Funguje zde i další zákon – Zákon symetrického pohybu, respektive Zákon zachování hybnosti:
Před výstřelem byla celková hybnost (p) nulová. Po výstřelu se hybnost objektu A rovná 0,341 pa = 0,395 · 0,862 = 0,341 a hybnost objektu B taktéž 0,341 pb = 0,605 · 0,563 = 0,341. Protože musíme na hybnost nahlížet „vektorově“ (má směr svého působení) a oba objekty se pohybují opačnými směry, je výsledná hybnost soustavy i po výstřelu nulová!
Celý děj tak respektuje zákony zachování energie i zachování hmotného středu!
Zde si můžete vytvořit obsah, který bude použit v rámci modulu.