3.5.8 SKLÁDÁNÍ RYCHLOSTÍ
Známe již rychlosti obou těles z interního (A, B) i externího (C) pohledu. Stále však nevíme, jakou rychlost naměří těleso A vůči tělesu B, stejně tak netušíme výsledek recipročního měření.
Obě tělesa se sice pohybují opačným směrem, ale vzhledem ke specifické geometrii časoprostoru nelze použít obyčejné sčítání.
Na tomto místě je třeba ujasnit, že problematika „sčítání“ rychlostí obecně zahrnuje dva zcela rozdílné pohybové stavy:
• Objekty se vzdalují od společného hmotného středu:
Scénář – dva vlaky se vzdalují od nádraží dvěma opačnými směry; výstřel z děla dle předchozí kapitoly atd.
• Objekty se pohybují kaskádovitě:
Scénář – po chodbičce pohybujícího se vlaku se pohybuje druhý malý vláček; po jedoucím transportním pásu na letišti běží člověk atd.
Situace jsou principiálně odlišné, a proto je popisují jiné matematické vztahy:
3.5.8.1 OBJEKTY SE VZDALUJÍ PŘÍMOČAŘE OD BARYCENTRA
V minulé kapitole jsme objasnili prostorovou kružnici dvou objektů vzdalujících se od společného hmotného středu – po shodné přímočaré linii. A právě v této pohybové situaci nás poprvé bude zajímat otázka „sčítání“ rychlostí. Prostorová kružnice nám ukázala, jaké rychlosti oběma objektům naměří externí pozorovatel (v bodě C) i jaké rychlosti naměří interně subjekty samy vůči barycentru (C), vyvstala však otázka, jakou rychlost naměří oba objekty (A, B) vůči sobě navzájem?
Pro vyřešení této úlohy je nejlepší si představit, že oba projektily za sebou odvíjí tenké srolované „měřidlo“, které v barycentru C objektivně rozhoduje, jakou vzdálenost urazily oba objekty v každém okamžiku. Technologická proveditelnost zde opět nehraje roli – je třeba pouze umět si tento experiment „vizualizovat“ – je jedno, zda si představíte navíjecí pásmo, provázek či tenké molekuly grafenu poskládané za sebe.
Začneme například určením rychlosti, kterou naměří přístroje A objektu B:
Objekt A se pohybuje z pohledu svého interního času rychlostí vac = 1,703 (za jednu sekundu urazí vzdálenost 1,703). Z pohledu externího pozorovatele v barycentru C však běží čas jiným tempem (z jeho pohledu se objekt A pohybuje pomaleji) a objektu A naměří odvíjející se měřidlo vzdálenost 1,703 až v čase 1,976 sekundy 1/0,506 = 1,976. Zároveň (v čase 1,976 sekund) naměří měřidlo v barycentru C druhému objektu B vzdálenost 1,113 sekundy 1,976 · 0,563 = 1,113.
Pro určení výsledné rychlosti A vůči B stačí délky obou měřidel sečíst, tedy:
vab = 1,703 + 1/0,506 · 0,563 = 1,703 + 1,976 · 0,563 = 2,815
Určit obecný vztah je snadné:
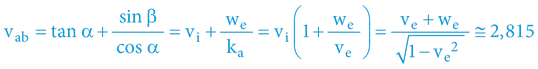
Známe-li obecný vztah, hravě určíme analogicky i rychlost, kterou naměří přístroje B objektu A:
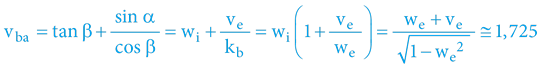
Vše opět nejlépe objasní diagram:
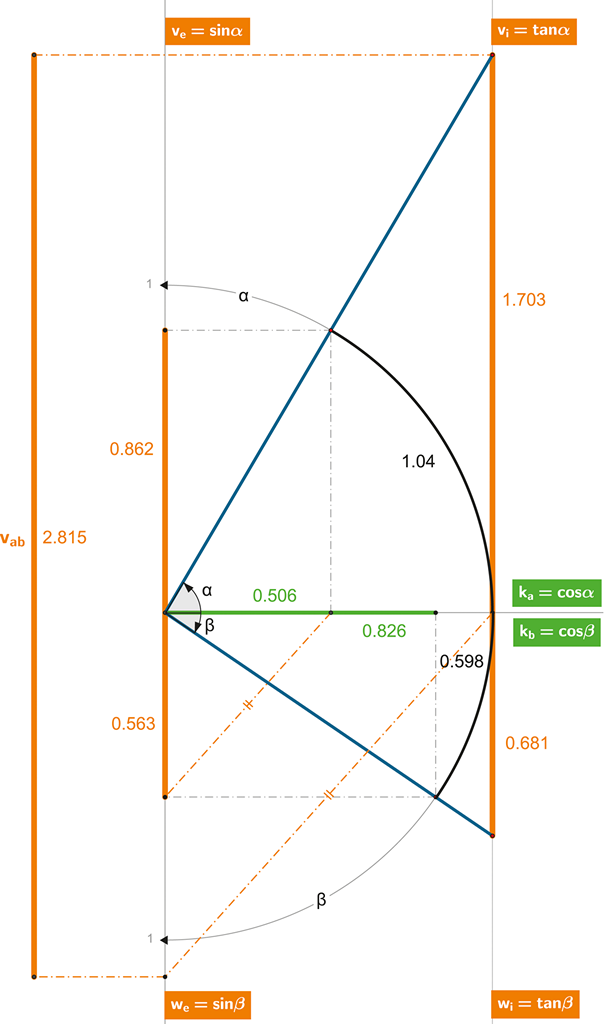
Obrázek 122 + ANIMACE:
Sčítání rychlostí lze provést i geometricky – s pomocí pravítka a rovnoběžek. Graf zobrazuje kvůli přehlednosti pouze konstrukci vab.
3.5.8.2 OBJEKTY SE POHYBUJÍ KASKÁDOVITĚ PŘÍMOČAŘE
V kapitole Sčítání rychlostí jsme (v rámci TR) pracovali s představou dvoustupňové kosmické lodi, jejíž první stupeň (A) dosáhne rychlosti 2·108 m/s (0,67 c) vůči pozemskému řídicímu centru (C), a následně z něj odstartuje druhý stupeň (B), který poletí ve stejném přímočarém směru a dosáhne téže rychlosti, tentokráte však vůči prvnímu stupni kosmické lodi (A). Jaká bude rychlost druhého stupně (B) vůči pozemskému řídicímu centru (C)?
Jednoduché sčítání rychlostí zde samozřejmě nemůžeme použít, korektní v této situaci není ani Einsteinův vzorec pro sčítání rychlostí – výsledná rychlost 0,92 c (276 923 km/s) není správný výsledek!
Situaci opět nejlépe objasní časoprostorová kružnice:
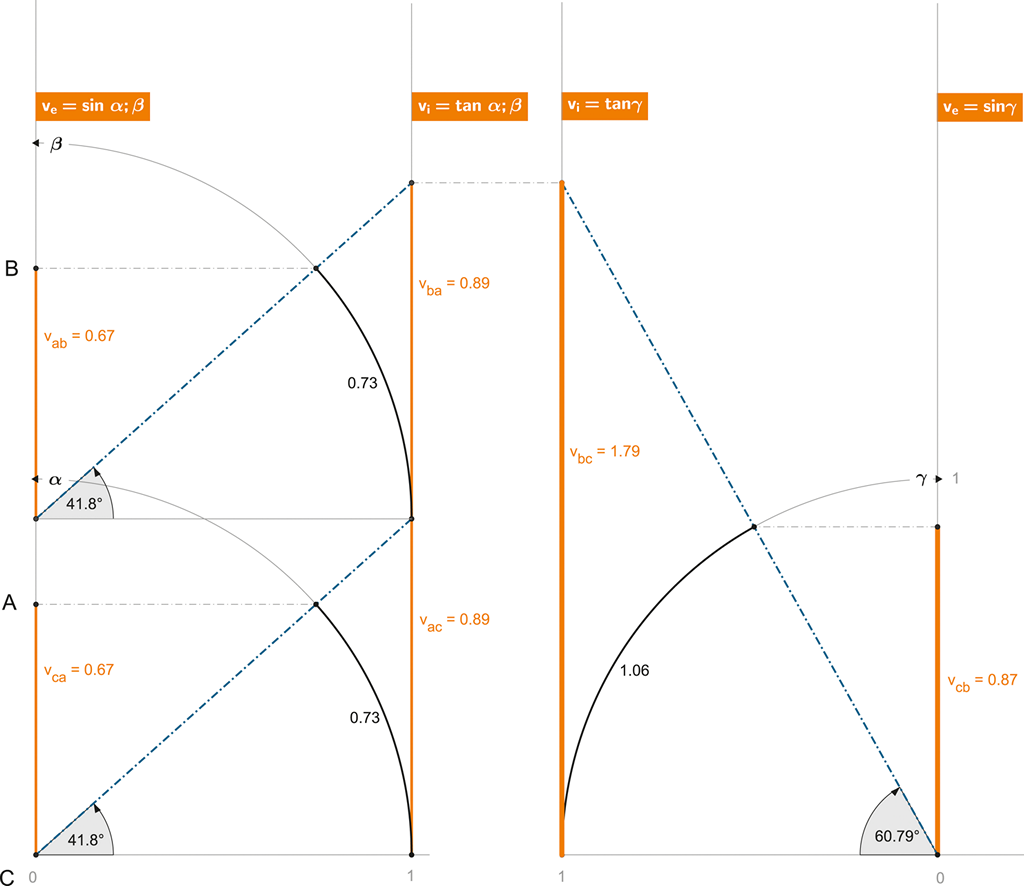
Obrázek 123 + ANIMACE:
Obě dílčí tangenty se prostě sečtou a výsledek převedeme zpět na sinus (externího pozorovatele).
Ve výsledku naměří interní účastník B svou rychlost vůči C v hodnotě 1,79 (5,4·108 m/s), zatímco externímu pozemskému řídicímu centru (C) se bude rychlost objetu B jevit v hodnotě 0,87 (261 860 km/s).
vbc = tan γ = vac + vba = tan α + tan β ≅ 1,79
vcb = sin γ = sin (arctan (tan α + tan β)) ≅ 0,87
3.5.8.3 PROČ JE RYCHLOST SVĚTLA LIMITOVANÁ?
Výšeuvedený princip „kaskádovitého“ skládání rychlostí je (mimo jiné) i dalším odůvodněním, proč se rychlost světla jeví (externím) pozorovatelům jako omezená (na hodnotě 3·108 m/s):
Neexistují žádná rychlostní omezení pro pohyb hmoty – jednorázovým pohybem či kaskádovitým skládáním pohybů se může hmotný objekt pohybovat neomezenou, respektive „nadsvětelnou“ rychlostí a transformuje-li se do elektromagnetického vlnění, pak se bude pohybovat rychlostí nekonečnou. Z pohledu externího pozorovatele se však bude taková rychlost jevit jako omezená (vlivem existence času, respektive vlivem existence 4D prostoru)!
Skutečnost, že čas je 4. rozměrem našeho prostoru, je důvodem, proč se rychlost pohybu jeví externím pozorovatelům jako omezená.

