FAKTA O SYSTÉMU GPS
Navigační systém GPS byl prvním satelitním navigačním systémem v historii a zaznamenal fenomenální technologický i obchodní rozvoj. S jeho pomocí dnes umí svoji zeměpisnou polohu určit nejen běžný automobil, ale i každý lepší telefon a často i váš fotoaparát; a to s přesností v řádu metrů. Vojenské či záchranářské aplikace GPS pak umí určit polohu s přesností desítek centimetrů. Jde o bravurní důkaz lidské vynalézavosti a vědeckého pokroku.
Samozřejmě si nesmíme myslet, že původní pohnutkou vývoje tohoto systému byly civilní aplikace:
Po druhé světové válce USA analyzovaly efektivitu svých zbraňových systémů:
Spojenci svrhli během 2. světové války na Německo cca 2 miliony tun bomb, které měly na svědomí skoro 1 milion civilistů! Většina bomb byla shazována z výšky cca 10 km – „přesnost“ bombardování byla proto velmi problematická a fakticky bylo nemožné ničit pouze průmyslové objekty.
Generalita USA proto začala záhy po válce pracovat na spolehlivém systému navigace, který by mohl být dostupný pro každou „bombu“ i každou „raketu“ … následoval vývoj systému GPS.
Existují odhady, že kdyby byl systém GPS dostupný v boji proti nacistům, stejného ničivého efektu (na německý průmysl) by bylo dosaženo pouze s 60 tisíci tun munice a civilní oběti by byly „pouze“ v řádu 5 000 osob!
Systém GPS začal pracovat pro armádu USA v roce 1973, postupně byl zdokonalován a v roce 1994 byl uvolněn i pro civilní použití. Dnes je GPS nepostradatelným pomocníkem v každodenních civilních situacích, v průmyslu i službách.
Základní funkčnost systému jsme popsali již v kapitole Jak funguje GPS, přesto je vhodné se ponořit poněkud hlouběji, a to s ohledem na proklamovanou tezi „GPS jako důkaz relativistických jevů“:
Je pravdou, že v matematickém aparátu systému GPS jsou skutečně používané tzv. „relativistické korekce“ – je však třeba porozumět jejich významu (na celkovou funkčnost systému) a jejich faktické fyzikální interpretaci:
Tzv. primární relativistická korekce je prostá frekvenční kompenzace – aplikovaná přímo na frekvenci atomových hodin na palubě satelitů. Pozemské řídicí centrum pracuje s frekvencí radiového signálu 10,23 MHz a primární „relativistická“ korekce spočívá ve zpomalení (frekvenční offset) atomových hodin satelitu o 4,5·10‒10 na 10,229999995 MHz. Toto „rozladění“ probíhá ještě před vypuštěním satelitu na oběžnou dráhu.
Po umístění satelitu na oběžné dráze navíc vždy probíhá „jemné doladění“ této frekvence tak, aby signál přijímaný na Zemi přesně odpovídal požadované pozemské frekvenci (10,23 MHz).
Primárně je touto „relativistickou“ korekcí tedy zajištěno, že vysílací anténa (satelitu) i přijímací anténa (Země) spolu komunikují na stejné frekvenci:
O něco málo nižší frekvence záření ze satelitu totiž vlivem „pádu“ v gravitačním poli Země získává energii (od gravitačního potenciálu Země), a protože frekvence záření je přímo úměrná jeho energii – má takovéto (původně zpomalené) záření při dopadu na Zemi přesně takovou frekvenci, jakou řídicí centrum Země požaduje.
Vysílání signálu ze Země na satelit probíhá analogicky opačně – signál ze Země je vysílán v nominální frekvenci, výstupem v gravitačním poli tento signál ztratí nepatrnou část své energie a při dopadu na anténu satelitu je tak jeho frekvence o stejně nepatrný zlomek menší.
V kapitole Pound-Rebka experiment jsme již objasnili, že uvedený jev je především důkazem Zákona zachování energie, nikoliv důkazem TR či „gravitační dilatace času“. V následující kapitole bude okomentováno podrobněji.
Tzv. sekundární relativistická korekce je (u systému GPS) propočtena přímo ve vašem GPS navigačním přístroji. Fakticky (principiálně) jde o korekci (mírně) eliptické trajektorie satelitu, respektive o korekci orbitální excentricity. Navzdory svému názvu je tato sekundární „relativistická“ korekce především zohledněním Dopplerova jevu!
Reálně pracují všechny navigační systémy s několika dalšími matematickými korekcemi, které jsou pro funkčnost systému mnohem důležitější. Kdyby se měl systém GPS spolehnout pouze na relativistické korekce (a nepoužíval jiné kompenzační mechanismy) – byl by nepoužitelný!
Kontinuálně tak složité výpočetní mechanismy systému GPS řeší například vliv ionosféry (na šíření elektromagnetického signálu), trajektorii satelitu mírně deformuje i pozice Slunce (nejspíš jde o slapové jevy) i solární vítr.
Pro velmi přesnou navigaci je třeba dokonce zohlednit (kompenzovat) i poziční rozdíl mezi umístěním antény satelitu a faktického hmotného středu satelitu (po vypočtené orbitě totiž fakticky krouží hmotný střed sondy, který je od antény vzdálen v řádu desítek centimetrů!). Tato kompenzace je však reálně jen těžko realizovatelná – vhledem ke stabilizačním pohybům sond (pro zajištění potřebného natočení solárních panelů sondy ke Slunci). Zjednodušeně řečeno – rozměry satelitů budou vždy jednou z příčin nepřesností systému GPS. Řešením do budoucna bude zmenšování satelitů či taková konstrukce satelitů, aby umístění komunikačních antén bylo přímo v „těžišti“ satelitů.
Fundamentální princip satelitních navigačních systémů je nicméně (navzdory výšeuvedenému) velmi jednoduchý a nikterak nesouvisí s pozemním časem – funkčnost spočívá v relativním porovnání rozdílu časů přijímaných ze satelitů, nikoliv na absolutní časové hodnotě!
Stačí, aby všechny satelity byly vzájemně synchronizovány – GPS přijímač nepotřebuje nic jiného ke korektnímu určení vaší zeměpisné polohy. I kdyby měly všechny satelity na orbitě posunutý čas o dvě hodiny – GPS přijímač ve vašem autě bude fungovat správně, pouze bude ukazovat o dvě hodiny jiný časový údaj!
Reálně je samozřejmě lepší, aby GPS satelity pracovaly s naším pozemským časem (UTC, TAI), neboť pak mohou sekundárně sloužit i jako zdroj velmi přesného (téměř atomového) času, a to kdekoliv na planetě.
Primárním požadavkem na funkčnost GPS je tudíž co nejpřesnější synchronizace všech satelitů na orbitě – a v této úloze nehrají „relativistické korekce“ žádnou roli, respektive časy satelitů se postupem času „rozcházejí“ závislostí, kterou sice umíme kvantifikovat, ale nemáme pro ni fyzikální interpretaci – máme pouze přibližné matematické metody, kterými umíme tento syndrom částečně „léčit“.
Na zeměkouli je dnes rozmístěno 20 monitorovacích stanic (IGS) takovým způsobem, že každý satelit je vždy viditelný alespoň z jedné stanice. Data z monitorovacích stanic pak proudí do Hlavní kontrolní stanice (MCS) v Coloradu.
Protože zeměpisná poloha všech 20 monitorovacích stanic je přesně známa, MCS kontinuálně porovnává údaje GPS přijímačů ve všech stanicích s realitou a v reálném čase tak analyzuje okamžitou chybovost celé technologie.
Systém tak neustále určuje reálné chyby v parametrech orbit a je-li zapotřebí (chyba je přílišná), posílá satelitům „navigační zprávu“. Součástí takové navigační zprávy jsou data pro zpřesnění faktické polohy satelitů (efemeridy), parametry ionosféry a korekční koeficienty pro atomový čas satelitů.
Korekční metodologie systému se přitom de facto neustále zdokonaluje, počítačové programy analyzují stále větší objemy dat – výsledkem jsou stále dokonalejší (avšak složitější) korekční výpočty.
Korekční časové koeficienty jsou založené na kombinaci lineárního a periodického matematického modelu časové chyby atomových hodin satelitů. Na základě vyhodnocování reálné chyby (porovnání s pozemním časovým standardem) jsou tyto koeficienty pravidelně upgradovány (přepočítávány) a odvysílány na satelit.
Atomové hodiny na palubách satelitů jsou tak tímto mechanismem pravidelně „seřizovány“.
Navzdory tomuto složitému algoritmu – inženýři dodnes hledají „reálný“ matematicko-fyzikální model, který by (v mezidobí mezi synchronizacemi) zajistil lepší přesnost hodin na palubách satelitů – čas na jejich palubách totiž neustále vykazuje lineární, periodické i náhodné anomálie!
Představa vyznavačů TR, že známe fyzikálně-matematický vzorec, který zajišťuje synchronizaci času satelitů vůči pozemskému času, je fiktivní a iluzorní – to jediné, co umíme, je měřit časové disproporce a následně vytvořit matematický model, který tyto disproporce (lépe či hůře) kompenzuje.
Čas od času někdo navrhne dokonalejší (a složitější) kompenzační mechanismus – na jehož základě GPS satelity zmenší svou vzájemnou časovou chybu – fyzika však v tomto procesu dnes již hraje pouze marginální roli – prim hraje matematická statistika a metody matematické analýzy dat.
Navzdory naivním a velmi zjednodušujícím představám – GPS není statický systém s přednastavenými parametry „z výroby“, nýbrž dynamický a multi-korekční mechanismus s vícečetnou zpětnou vazbou, který „sám sebe“ reguluje (v rámci implementovaných korelačních vzorců a matematických konstrukcí).
Pro příklad:
V dnešní době je chyba v určení orbity satelitů systému Glonass (Rusko) cca 20 cm a chyba v určení času cca 0,4 ns. Starší a „vychytanější“ systém GPS (USA) je na tom lépe – jeho chybovost je cca poloviční. V době míru spolu oba systémy kooperují, sdílí data a moderní navigační přijímače tak pracují s kombinací obou systémů na ještě přesnějším určení pozice.
Fyzikálním principem celého systému je metoda triangulace, respektive trilaterace – fundamentem jsou matematické funkce, které mají základ ve výpočtu trojúhelníku – jde o trigonometrii!
Sama trigonometrie je založená na principu pravoúhlého trojúhelníku, respektive na Euklidovském prostoru (pravoúhlém časoprostoru).
99 % všech výpočtů v systému GPS se spoléhá na „rovnou“ Euklidovskou matematiku, a proto je funkčnost celého systému důkazem „tradičního“ pravoúhlého prostoru, nikoliv prostoru jakkoliv zakřiveného!
V neposlední řadě je nutné zmínit ještě jeden opomíjený fenomén:
Příznivci TR proklamují, že systém GPS dokazuje, že relativní pohyb jedněch hodin vůči druhým způsobuje objektivní časové posuny (Ano – již v tomto tvrzení se skrývá paradox).
Na orbitě GPS se však pohybuje celkem 24 satelitů, každý po jiné trajektorii (některé satelity si letí naproti, jiné se od sebe vzdalují), a tudíž s rozdílnými rychlostmi „relativně“ vůči sobě navzájem.
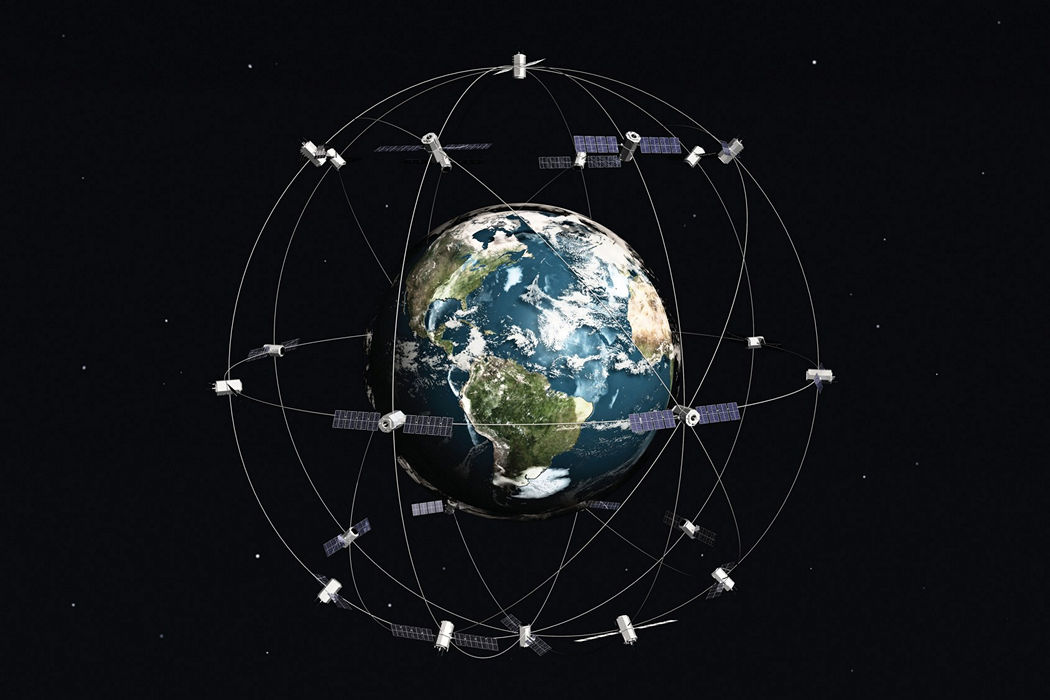
Obrázek 151:
Satelity na orbitě se „relativně“ pohybují vůči sobě velmi rozdílnými rychlostmi.
(zdroj: Wikimedia)
Jak je možné, že interní čas všech těchto satelitů se daří udržet celkem velmi dobře synchronizován? Vždyť se tyto satelity pohybují vůči sobě zcela rozdílnými rychlostmi?!
Jde o další „paradox“ TR, respektive o dva paradoxy v jednom jediném tvrzení!

