3.6.4 GRAVITACE DLE NEWTONA
Newton ve své mysli přemítal nad velmi složitými problémy a scénáři – v tomto ohledu překonal nejen všechny své předchůdce, ale (zdá se) i všechny své následovníky – spojením geniálního fyzikálního a geniálního matematického myšlení v synergickém efektu.
3.6.4.1 TEORETICKÉ ÚVAHY NEWTONOVA GÉNIA
Problém gravitace objasnil Newton mimo jiné i pomocí své slavné úvahy o děle střílejícím projektily až na oběžnou dráhu Země. Newton však brilantně vyřešil i mnohem komplikovanější úlohy – jež dodnes dokládají hloubku Newtonových úvah a jsou věčnou inspirací na cestě k pochopení gravitace:
1. Newton si například kladl otázku, jak by probíhal pád předmětu do „studny“, která by vedla kolmo skrz celou zeměkouli? Pomocí integrálního počtu spočítal všechny fáze letu – počáteční rovnoměrně zrychlený pád, následné zpomalování po průletu středem Země, vše „končící“ plným zastavením pádu předmětu na úrovni protilehlého ústí studny – načež ihned následuje opačný pohybový proces.
Newton pochopil, že pohyb předmětu by byl v takovémto scénáři analogický kmitavému pohybu na pružině a zcela exaktně spočetl časovou délku jedné periody (tam a zpět).
2. Stejně tak si Newton kladl otázku, jak bude probíhat pohyb, když nepůjde o kolmou studnu, ale pouze o šikmý tunel, který by vedl skrze část zeměkoule. Takovým tunelem by bylo možno vybudovat „vlakové spojení“, které by fungovalo „zdarma“ – pohybovalo by se pouze silou gravitace (zanedbáme-li odpor prostředí).
Pohybem po nakloněné rovině by vlak zrychloval, v polovině tunelu by jel konstantní rychlostí a následně by jej gravitace opět brzdila tak, aby na druhém konci tunelu vlak sám zcela zastavil, načež by začal couvat.
Newton opět provedl své výpočty a opět určil zcela exaktně časovou délku jedné periody (tam a zpět).
3. Třetím bravurním „kouskem“ Newtona bylo specifické řešení jeho scénáře s dělem:
Při určité konkrétní rychlosti výstřelu lze navést střelu na oběžnou dráhu kolem Země – v bezprostřední blízkosti jejího povrchu (opět musíme zanedbat odpor atmosféry, anebo použít malou planetku bez atmosféry). Takový projektil pak bude věčně obíhat planetu těsně u povrchu – přitažlivá síla se přesně vyrovná se silou odstředivou, respektive v každém okamžiku projektil „spadne“ o přesně takovou vzdálenost, o jakou se od povrchu vzdálí.
Newton opět vypočetl potřebnou rychlost pohybu i časovou délku periody jednoho oběhu kolem planety.
A nyní to nejlepší:
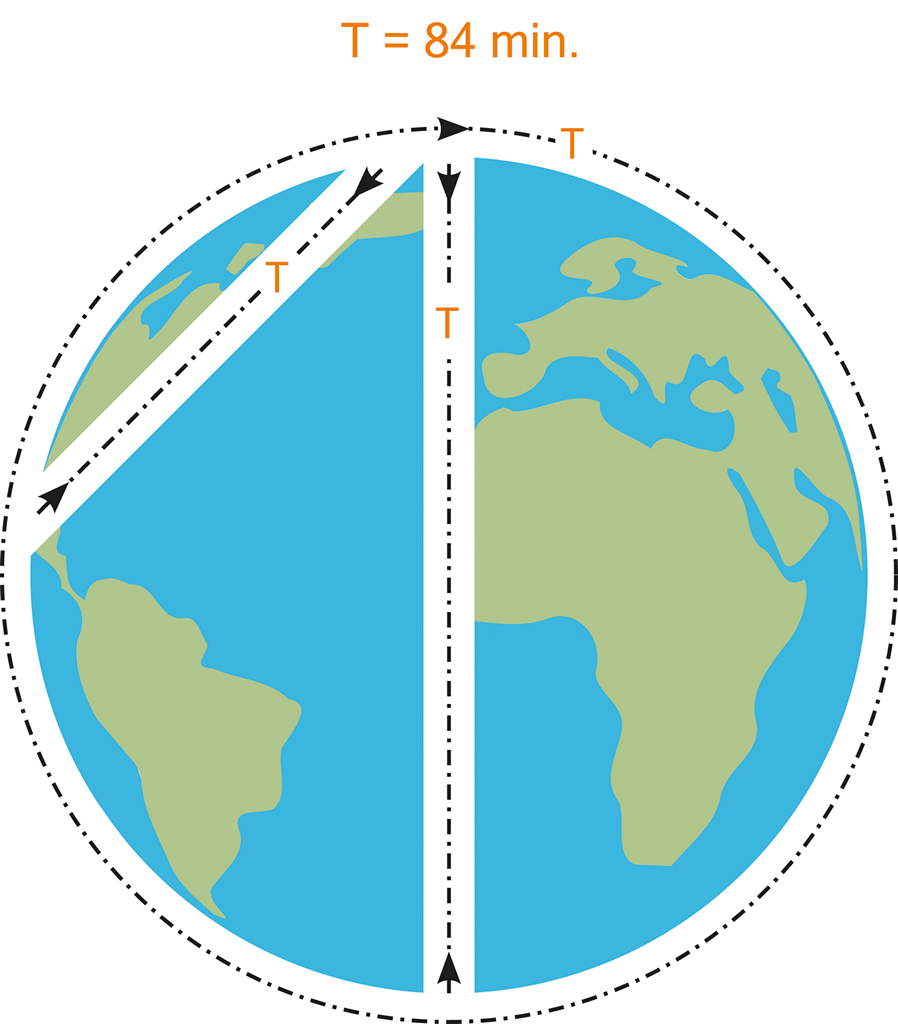
Obrázek 127:
Princip Newtonových geniálních úvah.
Newton analyticky dokázal, že ve všech třech výšeuvedených scénářích – bude časová délka jedné periody totožná!!!
Nezáleží na úhlu, pod kterým šikmo provrtáme zeměkouli pro gravitační vlakový spoj, nezáleží na hmotnosti kamene vhozeného do „studny“, na hmotnosti vlaku či na hmotnosti vystřeleného projektilu:
Celá perioda bude ve všech třech scénářích trvat stejně dlouho, a to 84 minut!
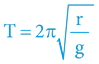
rpoloměr Země
gtíhové zrychlení planety
Je lhostejno, zda skočíte do kolmé studny, vydáte se pod libovolným úhlem po šikmé ploše gravitačním vlakem, anebo naskočíte na satelit kroužící kolem Země – ve všech třech případech budete cestovat „zdarma“ (bez jakéhokoliv pohonu) – a ve všech třech případech se vrátíte do výchozího místa za stejnou dobu (84 minut v případě Země).
Tak dokonalá je gravitace – tak geniální jsou postřehy Newtona!
Znovu a znovu musíme vzdávat hold člověku, který takto komplexně pochopil gravitaci. Newton formuloval fyzikální principy i odvodil potřebné matematické vztahy. Kladl si otázky jako nikdo před ním a téměř ihned na ně nacházel odpovědi.
Myšlenky na pohyb tělesa uvnitř provrtané zeměkoule můžeme najít již u Leonarda da Vinciho, Newton však tuto problematiku popsal nejen teoreticky, ale zcela exaktně i matematicky – a to vše v roce 1687!
Zdá se pravděpodobné (navzdory soudobé nadutosti), že dodnes lidstvo neví o gravitaci tolik, jako věděl Isaac Newton!
3.6.4.2 ZÁKLADNÍ PRINCIPY GRAVITACE DLE NEWTONA
Newton formuloval, že dvě tělesa se přitahují silou, která směřuje do těžiště těles, je přímo úměrná součinu hmotností a klesá s kvadrátem vzdálenosti.
Newton tak (mimo jiné) objasnil, že ono Galileem naměřené pozemské tíhové zrychlení (g) není faktickou konstantou, ale závisí na hmotnosti Země a vzdálenosti od jejího těžiště (středu). Naše znalosti o gravitaci se tak díky Newtonovi velmi rozšířily, a navíc získaly zcela exaktní formulaci a matematický tvar.
Velmi zjednodušeně formulováno, nám Newton zanechal ke gravitaci tento odkaz:
F = m g
Gravitační potenciál (značíme jej V a v rámci TČ je definován kladně, nikoliv záporně!) je velmi důležitý pojem, který je dobré si zapamatovat:
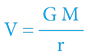
Mimo jiné nám používání gravitačního potenciálu zjednoduší mnoho vzorců:
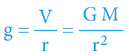
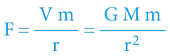
Rychlost volného pádu tak nově od dob Newtona již nebyla závislá pouze na čase, nýbrž je závislá na vzdálenosti od Země, respektive na rozdílu gravitačního potenciálu, v němž se pád (z výšky „h“) odehrává:
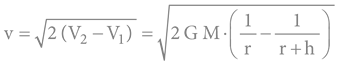
V teoretickém případě volného pádu z nekonečna (zatoulaný meteorit) se uvedený vzorec zjednoduší na tvar:
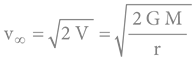
Mhmotnost Země (6·1024 kg)
Ggravitační konstanta (6,67·10‒11 N·m2/kg2)
rpoloměr Země (6,4·106 m je i vzdáleností k jejímu těžišti)
Vgravitační potenciál (V = GM/r)
hvýška volného pádu
Poznámka:
Na obrovském Newtonově přínosu pochopení gravitace nemění nic ani skutečnost, že hmotnost Země a velikost Gravitační konstanty experimentálně určil až jeho nástupce Cavendish – učinil tak právě na základě Newtonových zákonů gravitace!
Newtonovi taktéž vděčíme za matematiku „kosmických rychlostí“ (dále i KR):
3.6.4.3 PRVNÍ KOSMICKÁ RYCHLOST
První KR je rychlost, kterou potřebuje těleso dosáhnout, aby obíhalo po kruhové dráze kolem planety (těsně nad povrchem planety). Na Zemi tato rychlost činí cca 7,9 km/s.
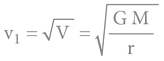
3.6.4.4 DRUHÁ KOSMICKÁ RYCHLOST
Druhá KR je minimální úniková rychlost z povrchu planety pro překonání její gravitace (aby se těleso trvale vymanilo z gravitačního vlivu planety). Pro Zemi je tato hodnota cca 11,2 km/s; pro Měsíc 2,3 km/s; pro Jupiter 59,6 km/s; pro Slunce 618 km/s.
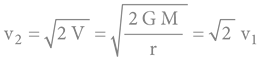
Druhá KR je totožná dopadové rychlosti objektu, který padá z „nekonečna“ (z natolik vzdálených míst vesmíru, kde je gravitace zanedbatelná) za předpokladu, že objekt byl na počátku pádu v klidu.
Všechny výšeuvedené vzorce Newtonovské fyziky popisují sice korektně náš „běžný“ svět – při velkých rychlostech (a energiích) však přestávají fungovat – v důsledku provázanosti 4D prostoru je nutné použít jinou matematiku!
3.6.4.5 OMEZENÍ KEPLEROVÝCH ZÁKONŮ
„Ve vědě, podobně jako v umění, musíme vědět, co smíme zanedbat.“
Igor Pomerančuk
Newton objasnil a dokázal, na jakém fundamentálním základě platí poznatky jeho předchůdců:
Jeho génius osvětlil, co určuje hodnotu gravitačního zrychlení (prvně změřené Galileem) i proč platí Keplerovy zákony nebeské mechaniky – proč se trajektorie nebeských těles tak nápadně přibližuje kuželosečkám (kružnice, elipsy, hyperboly, paraboly).
Vše přímo souvisí s tím, že gravitační síla klesá s druhou mocninou vzdálenosti, respektive gravitační potenciál klesá s její první mocninou (obě tvrzení jsou totožná).
Newton silou svého intelektu „od stolu“ exaktně (analyticky) objasnil vzorce, k nimž Kepler došel na základě dlouholetých astronomických pozorování tak trochu „ad hoc“. V tomto ohledu se zde naplno projevila skutečnost, že Newton byl nejen největším fyzikem své doby, ale zároveň i největším matematikem (snad jen Leibniz se mohl ve své době postavit Newtonovi v matematice)!
Newton si byl taktéž vědom faktu, že matematika nikdy nebude schopna analyticky (zcela přesně) postihnout reálný pohyb nebeských těles – protože těles je ve vesmíru více nežli dvě a nikdy nejsou dokonale kulatá a dokonale homogenní!
Kdyby byla v prázdném vesmíru pouze dvě tělesa (dokonale kulatá a hmotnostně homogenní) – pak by byla nebeská mechanika zcela a dokonale předpověditelná. Newtonova matematika totiž dokázala, že tato dvě tělesa by kolem sebe vzájemně obíhala (vůči sobě navzájem, nikoliv však vůči společnému barycentru) po kuželosečkách, respektive po elipsách (nejčastější varianta kuželosečky ve vesmíru). Takováto trajektorie by byla pravidelná, neměnná a věčná!
Newton však věděl, že reálný vesmír se bude „dokonalým“ kuželosečkám vždy pouze blížit (více či méně), neboť těles je ve vesmíru mnoho, a navíc nejde o dokonalé homogenní koule. Autor Zákona akce a reakce taktéž chápal, že nejen lehká tělesa obíhají ta těžká, nýbrž částečně je tomu i naopak – že pohyb je vždy symetrický!
Například přitažlivost Slunce tak sice hraje primární vliv na trajektorii Země (snažíc se vytyčit téměř dokonalou elipsu), ale ostatní planety se taktéž snaží svou silou přitáhnout si Zemi (a Země se snaží přitáhnout si ostatní planety) – takže výsledkem je lehce pokřivená elipsa, která se navíc s každým oběhem Země kolem Slunce trochu pootočí (ve směru oběhu). Stáčení elipsy je v astrofyzice známým fenoménem a odborně je označováno jako stáčení perihelia či precese perihelia (perihelium ≈ místo eliptické trajektorie, ve kterém je planeta Slunci nejblíže).
Kromě stáčení eliptických drah vykazuje trajektorie planet i další nepravidelnosti a odchylky od matematiky kuželoseček. Newton si byl samozřejmě tohoto faktu vědom a stejně tak chápal, že důvodem těchto poruch není chyba v gravitačním zákoně, ale skutečnost, že reálný hmotný vesmír je natolik komplikovaný a provázaný, že jej naše matematické znalosti neumí analyticky (přesně) popsat, respektive – že je to matematicky nemožné!
V tomto ohledu neučinila matematika od dob Newtona de facto žádný pokrok. Studium pohybu více nebeských těles se označuje jako „problém n-těles“. Tento problém již není analyticky řešitelný ani v případě pouhých 3 objektů. V naší Sluneční soustavě je přitom minimálně 10 velmi hmotných těles (v řádu alespoň 1022 kg) plus tisíce menších (nikoliv však zanedbatelných) asteroidů, planetek a komet!
Jediným možným řešením výpočtu nebeské mechaniky je tak přibližná „kombinovaná“ metoda zjednodušování, zanedbávání a separování (novodobě v kombinaci s výpočetní silou výkonných počítačů):
Analyticky popíšeme pohyb planety vůči nejtěžšímu objektu (Slunci), tím dostaneme rovnici kuželosečky a následně se pokusíme spočítat všechny korekce trajektorie tím, že najdeme matematickou funkci, která s co nejmenší chybou určí „poruchovou“ funkci každého nebeského objektu, jenž gravitačně ovlivňuje pohyb planety. Takových objektů je samozřejmě mnoho – a tak se zpravidla do výpočtu zahrnou jen ty nejbližší a nejtěžší objekty, protože si nějak dokážeme spočítat, že ty ostatní již mají „zanedbatelný“ vliv.
Matematicky uvažujícímu člověku je zřejmé, že v tomto ohledu je astrofyzika ve velkých potížích – neznámých je v této rovnici mnohem více nežli známých. Úloha je „řešitelná“ pouze s velkými kompromisy a mnoha předpoklady (z nichž mnohé mohou být zcela mylné):
Snažíce se spočítat odchylky od eliptické dráhy pro konkrétní planetu, musíte kalkulovat s tím, že dráhy ostatních (ovlivňujících) těles eliptické jsou (víte, že nejsou). Počítáte s tím, že nebeská tělesa jsou dokonale kulatá a hmotnostně homogenní (víte, že nejsou). Počítáte s tím, že zploštění rotačního elipsoidu Slunce je „zanedbatelné“ (víte, že o tom nic nevíte). Počítáte se „Slunečním větrem“, s vlivem nehomogenního pásu asteroidů, zanedbáváte slapové síly, … děláte, co můžete!
V tomto ohledu je potřebná určitá pokora v případech, kdy hodláte interpretovat výsledky svých výpočtů – musíte si být vědomi onoho příliš velikého množství předpokladů a příliš mnoha „zanedbávání“.
Mimochodem – kde zjistíte „skutečné“ hmotnosti nebeských objektů?
Nejsou vypsány v žádném „lexikonu“. Lze je pouze vypočítat. Jak?
Na základě Newtonova gravitačního zákona samozřejmě! Na základě oběžných drah okolních nebeských těles (jejichž hmotnost jste vypočítali sledováním jiných okolních těles, jejichž hmotnost jste vypočítali sledováním jiných okolních těles, jejichž hmotnost jste vypočítali sledováním jiných okolních těles atd. atd).
Z těchto důvodů se taktéž v čase měnily (a mění) udávané hmotnosti těles v naší Sluneční soustavě s tím, jak dalece jsme dokázali zpřesňovat naši přibližnou a zjednodušenou matematiku.
Ano – žijeme sice v době počítačů – ale počítač je jen stroj, který nepřemýšlí a výpočty dokáže provádět pouze na základě algoritmů, které mu sdělil astrofyzik. Počítač počítá jen s takovými rovnicemi a čísly, které do něj zadáme – respektive vždy počítá pouze s přibližnými hodnotami a idealizovanými fyzikálními algoritmy.
Výšeuvedenému navzdory – dal Newton svým následovníkům do ruky zákon, který evidentně funguje korektně a jediným praktickým omezením našich znalostí je složitá provázanost nebeské mechaniky a z toho plynoucí omezení matematického řešení.
Postupem času se tak chyba našeho zjednodušeného matematického modelu stále zmenšuje – čím dál více se tak můžeme na jeho „předpovědi“ spolehnout. Pohyby velkých hmot postihuje náš matematický model úspěšně, a tak jsme díky matematickým výpočtům časem objevili nová kosmická tělesa či zpřesnili údaje o hmotnosti (a vzdálenosti) těch již známých.
S každým dalším objevem se následně náš matematický model vylepšuje (chyba zmenšuje) – a díky tomu astrofyzika během dvou století zaznamenala obrovské pokroky (z velké části i díky technické revoluci – rozvoji elektrotechniky, kosmonautiky a počítačů).
Například kolem roku 1840 astronomové zaznamenali, že Uran (v té době poslední známá planeta SS) se při svém pohybu poněkud odchyluje od vypočtené trajektorie. V takových chvílích věda vždy znovu a znovu inklinuje k témuž scénáři:
„Newton se mýlil! Je třeba provést nějaké matematické korekce jeho zákona, aby naše výpočty souhlasily s pozorováním.“
Podobný postoj opakuje vědecká obec napříč historií poměrně pravidelně.
Časem se však vždy ukáže, že pozorovanou anomálii může vysvětlit právě a jen Newtonův zákon gravitace – že pozorovaná anomálie není jeho vyvrácením, ale naopak je jeho potvrzením!
I v případě „poruch“ dráhy Uranu nebylo důvodem ani zakřivení časoprostoru, ani Temná hmota (kupodivu):
Časem vyšlo najevo, že abnormální chování Uranu lze plně vysvětlit gravitačním působením ještě vzdálenější (dosud neobjevené) planety. Tato teoreticky předpovězená planeta byla zakrátko skutečně objevena – svět objevil Neptun – respektive jej objevil Urbain Le Verrier. Tento (francouzský) matematik roku 1846 vypočetl existenci a polohu planety Neptun a jeho předpověď byla záhy astronomicky potvrzena.
Málokdy si uvědomujeme, že nešlo ani tak o úspěch astronomie, ale především o úspěch Newtonovské fyziky!
Dnes známe svůj „domov“ již poměrně dobře a následující tabulka nám připomene jeho základní parametry tak, jak jsou známé v této době (2016):
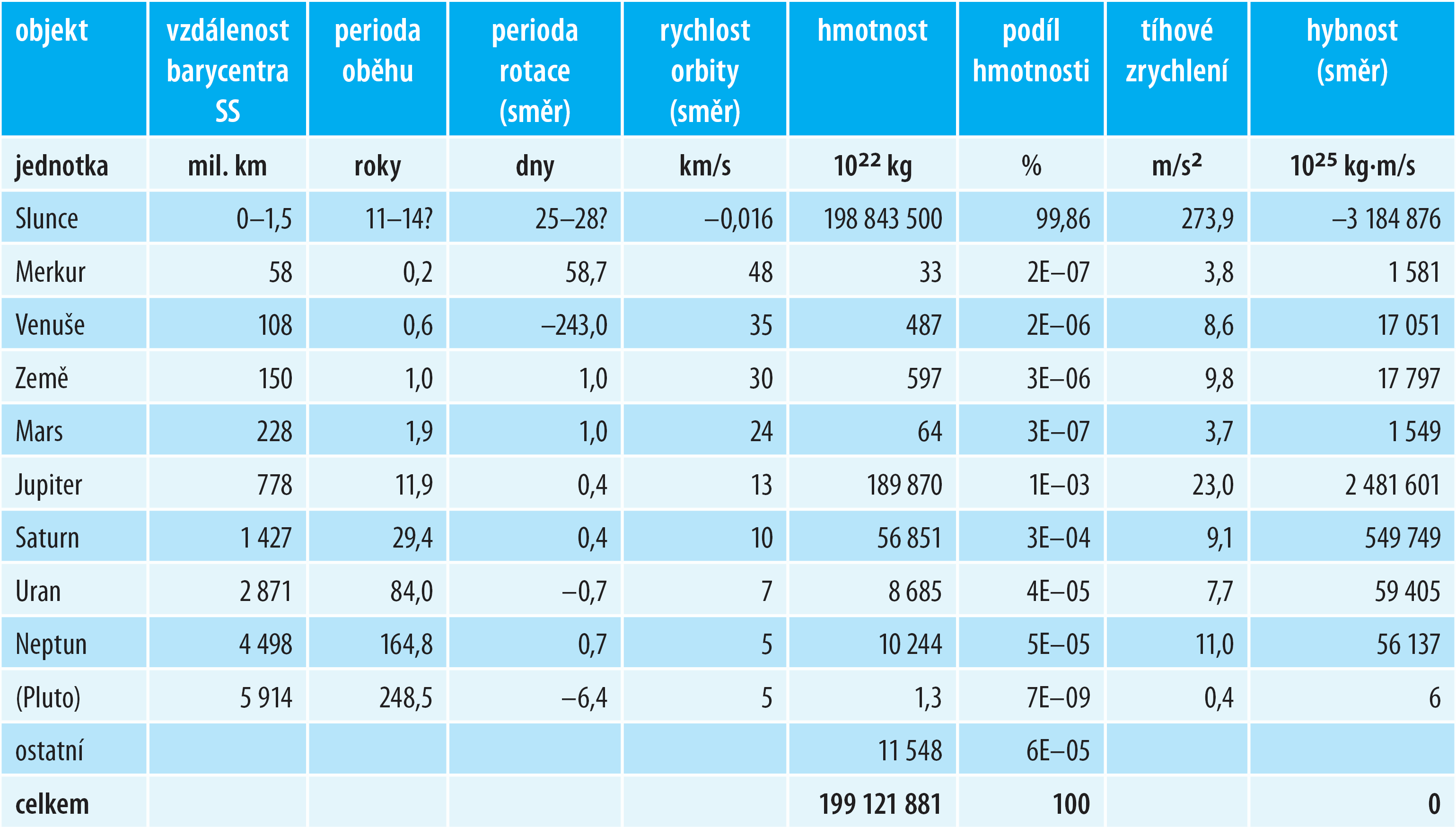
Tabulka 7: Současná známá čísla o naší Sluneční soustavě
Samozřejmě je výšeuvedená tabulka jen velmi „hrubým“ obrazem složitosti naší SS, která ve skutečnosti navíc obsahuje cca milion planetek a další miliony menších asteroidů. I komet je v naší soustavě na miliony (přes tisíc jich máme zmapovaných). Berme proto především předposlední řádek tabulky (ostatní) jako velmi nejistý!
Nedávno objevené „poruchy“ drah Neptuna, Pluta či planetek v Kuiperově pásu navíc naznačují, že daleko za orbitou Pluta se nachází další (dosud neznámá) velmi masivní planetka (až desetinásobek hmotnosti Země!). I v naší SS je stále co objevovat!
Ústředním i „středním“ objektem naší SS je Slunce, které všemu zcela hmotnostně dominuje (cca 99,86 % hmotnosti SS), a určuje tak hlavní rysy nebeské mechaniky – všechno musí obíhat kolem Slunce!
Proto nazýváme model naší vesmírné soustavy heliocentrickým – protože všechna nebeská tělesa obíhají kolem centrálního Slunce, jež tvoří nehybné „ohnisko“ eliptické trajektorie (obecně jde o kuželosečky) všech objektů SS.
Tak to dnes píšeme v každé učebnici …
… není to však pravda!
Výšeuvedené tvrzení je platné jen z poloviny!

