3.6.14 CO VYJADŘUJE ZÁHADNÁ GRAVITAČNÍ KONSTANTA?
„Všechny zásadní pravdy procházejí třemi stadii. Nejprve jsou zesměšňovány, pak zuřivě vyvraceny, aby byly nakonec přijaty jako samozřejmost.“
Arthur Schopenhauer
Gravitační konstanta G nás provází životem zpravidla již od střední školy, a věnujeme-li se fyzice aktivně, pak ji potkáváme téměř „na každém kroku“. Opět se naskýtá otázka: Proč je gravitační konstanta taková, jaká je?
Analogicky podobné otázce pro hodnotu rychlosti světla – i v tomto případě platí, že gravitační konstanta není tajemným fenoménem – čekajícím na své odhalení.
Hodnota G opět pouze „koriguje“ naše fyzikální zákony s ohledem na to, jak nesystematicky a nekonzistentně jsme si kdysi zvolili „základní“ fyzikální jednotky (SI) – konkrétně v tomto případě kilogram a sekundu:
Znovu jde o to, že perioda rotace naší planety (od níž je sekunda původně odvozena) nemá žádný kauzální vztah k hmotnosti jednoho litru vody (tato původní definice kilogramu je dnes nahrazena „definicí“ odkazující na prototyp kilogramového etalonu, který trůní ve formě slitiny platiny a iridia kdesi ve sklepním trezoru BIMP nedaleko Paříže).
Celou „záhadu“ gravitační konstanty navíc komplikuje „nepořádek“ v metodologii fyzikálních konstant:
Fyzikální nadšenci již možná zaznamenali anomálii, kdy tradiční vzorce pro výpočet elektrické a gravitační síly jsou principiálně podobné, a přesto odlišné:
Coulombova síla: 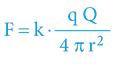 ; kde
; kde 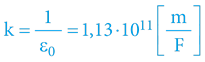
Newtonova síla: 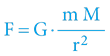 ; kde
; kde 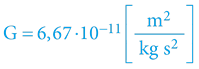
V obou vztazích vystupuje (kromě vzdálenosti, nábojů či hmotností) i specifická konstanta (permitivita či Gravitační konstanta), pouze u Coulombova vztahu je zde však navíc faktor 4π!
Tato anomálie je opět dokladem toho, jak z „úcty k tradici“ věda občas rezignuje na systematičnost a řád. Korektní je přitom výraz Coulombův, neboť faktor 4π zde odkazuje na skutečnost, že silové působení probíhá v Euklidovském 3D prostoru (v délkovém kontextu). Tato skutečnost se přitom samozřejmě netýká pouze elektrostatických sil, ale i sil gravitačních a obecně – jakéhokoliv „polního“ působení:
Umístíme-li do prostoru 100W žárovku a rozvineme-li ve vzdálenosti 1 metru solární panel o ploše 1 m2, pak tímto panelem zachytíme pouze 8 % světla (energie) žárovky, respektive 1/13, respektive 1/4π! Vše samozřejmě souvisí se vzorcem pro výpočet povrchu koule – kuloplocha s poloměrem jednoho metru má povrch cca 13 m2.
Faktor 4π proto patří do každého fyzikálního vzorce pro „polní interakce“ ve 3D světě, neboť kvantifikuje, jak moc klesá intenzita „účinku“ se vzdáleností.
Faktor 4π má tedy původ v geometrických poměrech našeho 3D světa. Kdyby byla plocha koule (o poloměru 1 metr) rovna 1 m2, pak by mohlo být vše jednodušší (magické číslo π by nebylo potřeba) – ale tak tomu není – stejně tak, jako obvod jednotkové kružnice není roven jedné!
Veledůležité číslo π bychom proto raději neměli ignorovat:
Přestože TČ původně definuje jednotkou energie kilogram (hmotnost považuje za pouhé synonymum pojmu energie), nyní provedeme finální zjednodušení soustavy jednotek TČ:
veličina:energie, respektive hmota, respektive hmotnost
značení:E
jednotka:spacegram (sg)
přepočet:1 sg = 3,21·1034 kg = 2,9·1051 J
Proč 3,21·1034? Co je to za číslo?
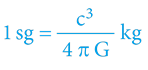
Zvolíme-li za jednotku hmoty (energie) 1 spacegram – vše bude o hodně smysluplnější a jednodušší, neb se jednou provždy zbavíme „obtěžující“ konstanty „G“:
Gravitační potenciál a jeho vztah k časoprostorovému úhlu:
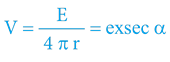
Přičemž máme na paměti, že funkci exsec na kalkulačkách nenajdeme a je praktičtější ji přepočítat na funkci cosinus:
Vztahy pro 2. kosmickou rychlost postačí pouze zopakovat:
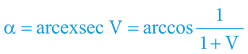
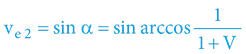
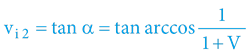
Gravitační rudý posuv a gravitační modrý posuv (kdy V2=0):
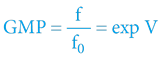
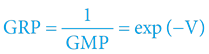
Na první pohled se může zdát výšeuvedená konstrukce poněkud „crazy“ – zvolit za jednotku energie (hmoty) tak „obrovskou“ hodnotu – vždyť i nejhmotnější známá hvězda ve vesmíru (R136a1) má v této nové jednotce energii pouhých 0,016 sg. Pročpak by měla být jednotka energie (hmotnosti) tak „nesmyslně“ obrovská?
Musíme však pochopit, že v tomto případě vše determinuje sekunda:
Jednotka energie nám vychází tak „astronomicky“ obrovská proto, že jsme si za jednotku prostoru (časoprostoru) zvolili obrovitánskou sekundu!
Věk (trvání) vesmíru odhadujeme na cca 4·1017 sekund. Délkový poloměr nám známého (viditelného) vesmíru se přitom odhaduje na cca 15·1017 sekund. Teprve v tomto kontextu pochopíme, jak „hrubou“ jednotkou je námi zvolená sekunda – rozlišení této jednotky totiž zhruba odpovídá vzdálenosti ze Země na Měsíc!
Hmota pozorovaného vesmíru (bez započtení temných sil) se přitom odhaduje na 1,5·1053 kg, tedy 47·1017 sg!
Teprve v tomto srovnání pochopíme, že námi nově definovaná jednotka množství hmoty (1 sg) je „obrovská“ pouze zdánlivě a ve skutečnosti je úměrná staré známé sekundě. Velikost (obrovitost či nepatrnost) je v tomto ohledu relativní (v pravém slova smyslu):
Množství hmoty v řádu 1034 kilogramu (cca 60 nejhmotnějších hvězd viditelného vesmíru) je stejně velkou/nepatrnou hmotností, jako je sekunda velká/nepatrná v celé historii trvání vesmíru – stejně tak, jako je „světelná sekunda“ velkou/nepatrnou délkovou vzdáleností v porovnání s rozměry viditelného vesmíru!
Chceme-li zachovat v našem novém systému jednotek alespoň sekundu (jakožto míru délkových a časových vzdáleností duálního časoprostoru), pak je spacegram jedinou smysluplnou jednotkou pro míru hmoty, respektive energie, respektive hmotnosti. Řádová „hrubost“ obou jednotek je de facto totožná (řád 1017)!
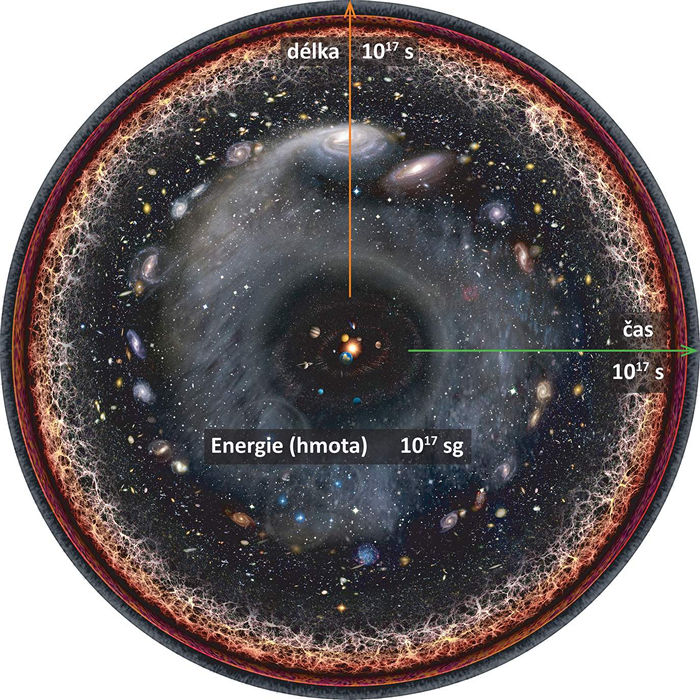
Obrázek 143:
Sekunda i spacegram jsou řádově totožně hrubé/jemné jednotky popisující náš vesmír.
(Zdroj: Wikimedia)
Poznámka:
Výšeuvedené hodnoty pro hmotnost, rozlehlost a trvání vesmíru je třeba brát s „dostatečnou rezervou“ – jsou výsledkem aktuálního kosmologického modelu, v němž hraje významnou roli „pokřivená“ relativistická geometrie (na základě nekorektní matematiky OTR pro gravitační rudý posuv počítáme hmotnosti vzdálených galaxií), ve vedlejších rolích zde opět vystupuje i Temná hmota a Temná energie.
Uváděná aktuální čísla tudíž nesmíme brát jako dogma – s opatrností snad mají alespoň „řádovou“ platnost. V tomto kontextu též chápejme i onu řádovou shodu pro rozměr sekundy a spacegramu.
Popíšeme-li náš vesmír v těchto nových jednotkách – je scénář jeho nebeské mechaniky jednodušší a prostý jakýchkoliv záhadných či „mystických“ konstant.
A co ostatní jednotky soustavy SI?
Ty se holt musí přizpůsobit!

