3.4.5 JEDNOTKOVÁ KRUŽNICE
Co je to rychlost?
Obecně vzato – rychlost je mírou pohybu, která nám sděluje, jak se mění délková trajektorie za jednotku času. Ve zcela exaktním vyjádření je rychlost derivací dráhy podle času v = ds/dt. Více dle definic TČ: Rychlost.
TČ vychází z myšlenky, že prostor představuje vzájemně provázanou jednotu délky a času (jež jsou navzájem kolmé). U délkové složky prostoru (časoprostoru) můžeme mluvit o délkové vzdálenosti, u časové složky o časové vzdálenosti, obecně pak u časoprostoru o časoprostorové vzdálenosti.
Minulé kapitoly objasnily, že tuto bipolární veličinu lze obecně měřit sekundami!
Ona vzájemná provázanost délky a času – respektive skutečnost, že rychlost udává změnu délkové vzdálenosti za jednotku času – je důvodem, proč „rychlost“ je v novém světě TČ bezrozměrnou veličinou sekunda/sekunda = 1.
Budeme-li proto dále pracovat po vzoru trigonometrie s jednotkovou kružnicí, je dle výšeuvedeného rychlost totožná s délkovou vzdáleností jednotkové kružnice časoprostoru (prostorového trojúhelníku)!
Vše nejlépe objasní následující nákres situace na „jednotkové kružnici“ časoprostoru:
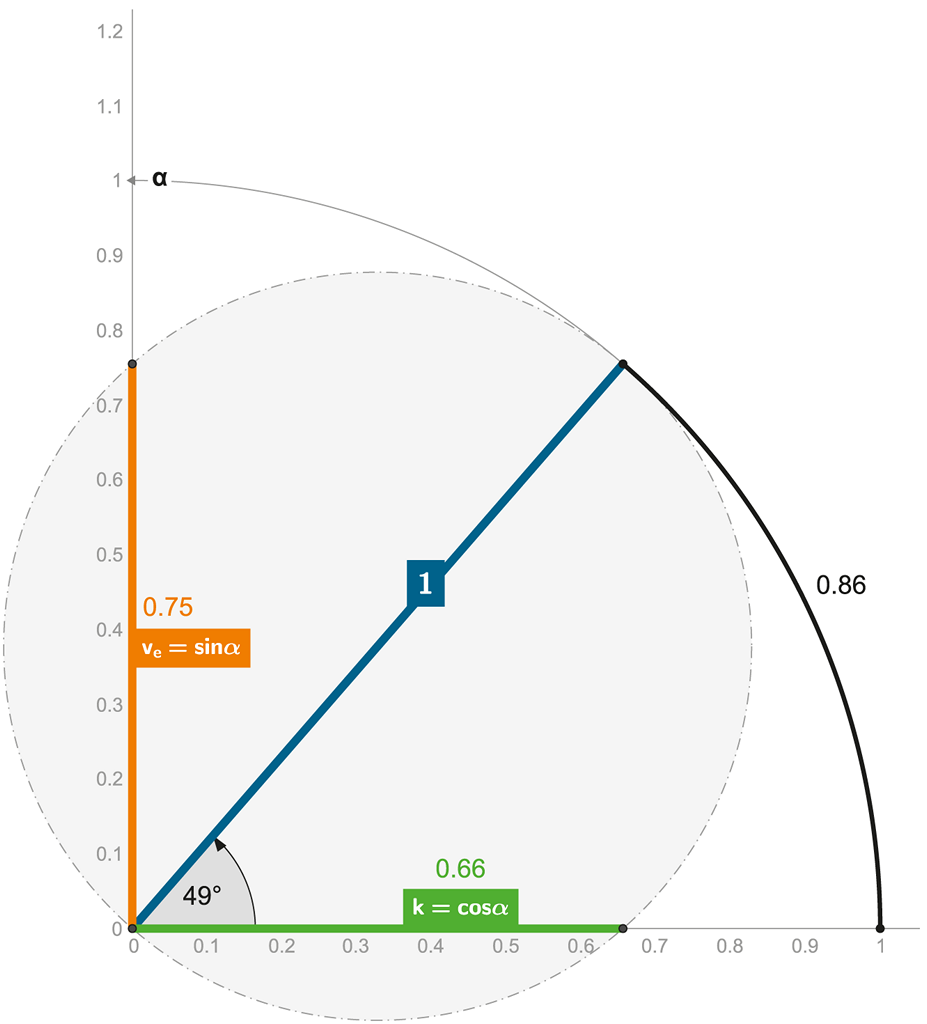
Obrázek 97 + ANIMACE:
Jsem jednotková kružnice a jsem velmi důležitá … seznamme se!
Jde o „kruhové“ vyjádření jednotkové kružnice – kde rotující kruh vymezuje jednotlivé trigonometrické funkce.
Zde jsme již opustili „příklad“ z minulých kapitol – následující grafy zobrazují jinou (více názornou) pohybovou situaci.
V knize však budeme raději používat „klasickou“ variantu, kdy získáme trigonometrické funkce pomocí rovnoběžek:
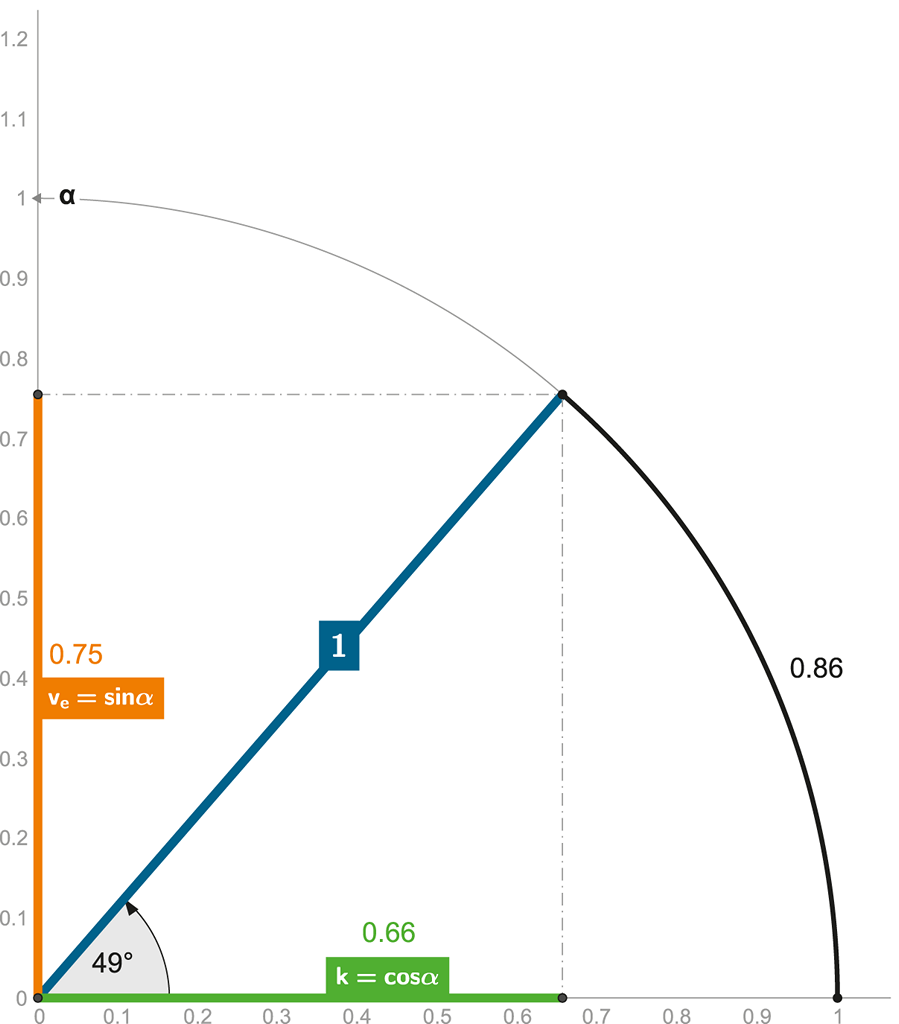
Obrázek 98 + ANIMACE:
I klasická varianta trigonometrické (čtvrt)kružnice spolehlivě definuje 4D časoprostor!
Časoprostorová kružnice vznikla tím, že jsme trigonometrické zobrazení na obrázku 94 celé vydělili časem (te).
Vodorovná osa (x) nám tedy nově zobrazuje koeficient časové kontrakce k = ti/te, svislá osa (y) vyjadřuje externí rychlost (délka dělená časem vyjadřuje rychlost).
Co vše tedy umí jednotková kružnice časoprostoru zobrazit?
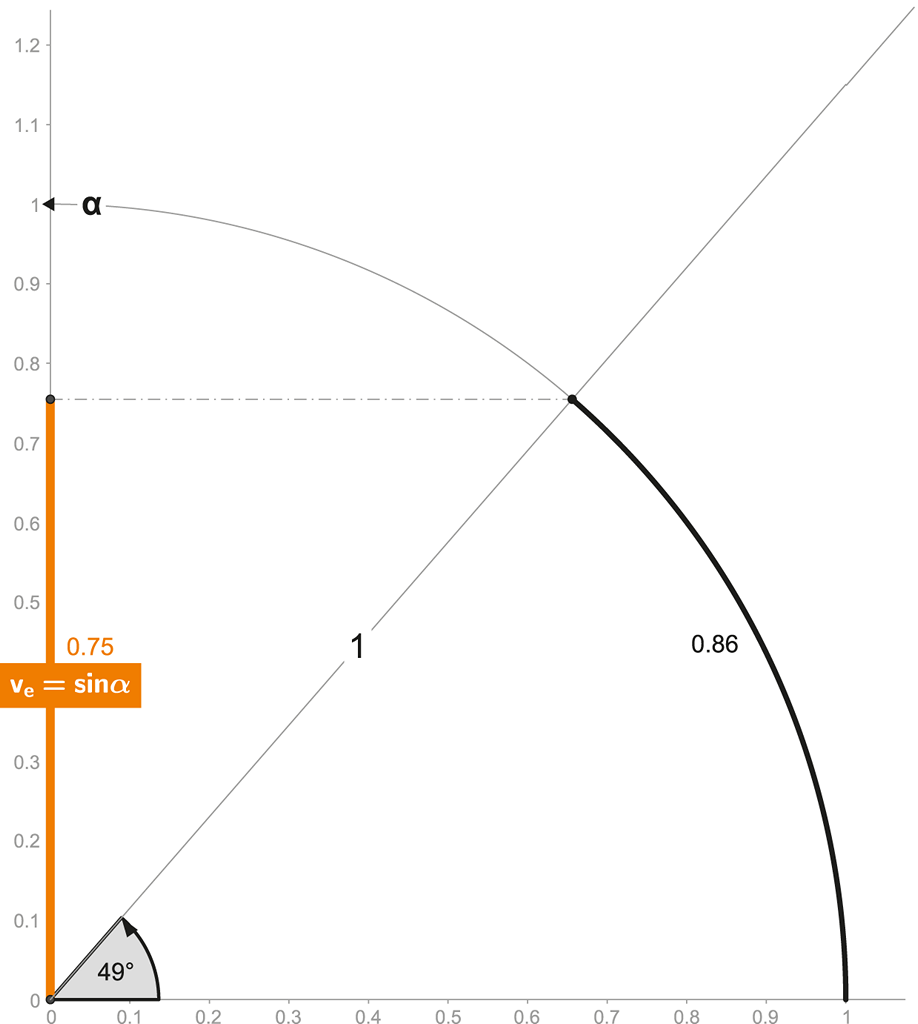
Obrázek 99:
Externě naměřená rychlost je sinem časoprostorového úhlu.
Technologie zatím bohužel neumožňuje lidstvu přímo (interně) se účastnit pohybů velikými rychlostmi, v tomto ohledu jsme zatím odsouzeni k roli pouhého externího pozorovatele – námi (externě) naměřená rychlost je tudíž (oranžovým) sinem časoprostorového úhlu a je vždy menší či rovna jedné!
ve = sin α α = arcsin ve
Jakmile tedy objektu naměříme externě nějakou rychlost – dopočítat časoprostorový úhel (α) je triviální:
V našem vzorovém případě (dle obrázku) lze snadno spočítat (či odměřit na časoprostorové kružnici), že naměříme-li externímu objektu rychlost 0,75 (75 % c), je časoprostorový úhel takovéhoto pohybového děje roven 0,86 rad (49°)!
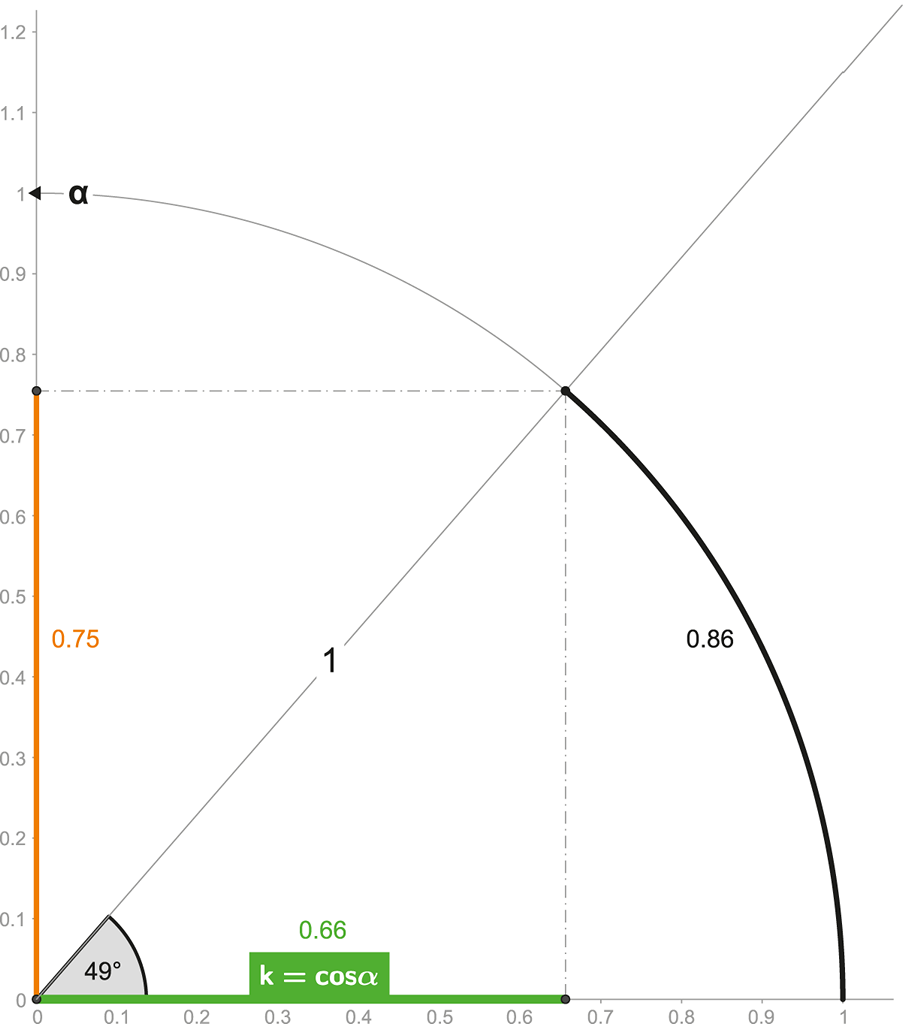
Obrázek 100:
Funkce cosinus časoprostorového úhlu určuje kontrakci času.
Zvýrazněná (zelená) linie určuje kontrakci (zkrácení) času – k – respektive určuje poměr, jak moc je čas interního účastníka děje „zpomalený“ vůči času externího pozorovatele. Tento poměr je cosinem časoprostorového úhlu, a je tedy vždy menší či rovný jedné!
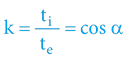
V našem vzorovém případě (dle obrázku) lze snadno spočítat (či odměřit na časoprostorové kružnici), že kontrakce času je 0,66!
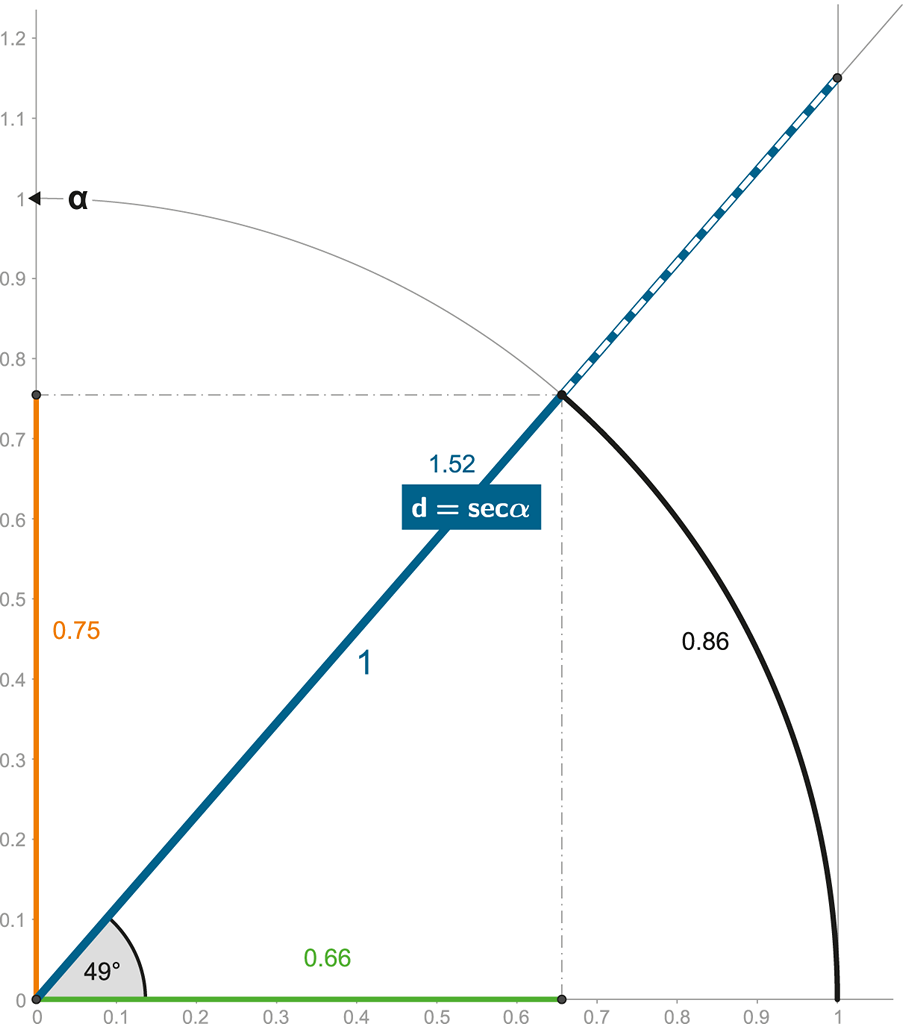
Obrázek 101:
Sekanta časoprostorového úhlu kvantifikuje dilataci času.
Zvýrazněná (modrá) linie určuje dilataci (prodloužení) času – d – respektive určuje poměr, jak moc je externí čas „zrychlený“ vůči času interního pozorovatele. Tento poměr je sekantou časoprostorového úhlu, a je tudíž vždy větší či rovný jedné!
Čerchovanou linií je znázorněno, o kolik sekanta převyšuje „jednotkovou“ jedničku – toto číslo je totiž velmi důležité – jak zjistíme později!
Dilataci času lze také spočítat jako inverzní funkci vůči kontrakci času:
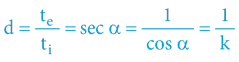
V našem vzorovém případě (dle obrázku) lze snadno spočítat (či odměřit na časoprostorové kružnici), že dilatace času je 1,52!
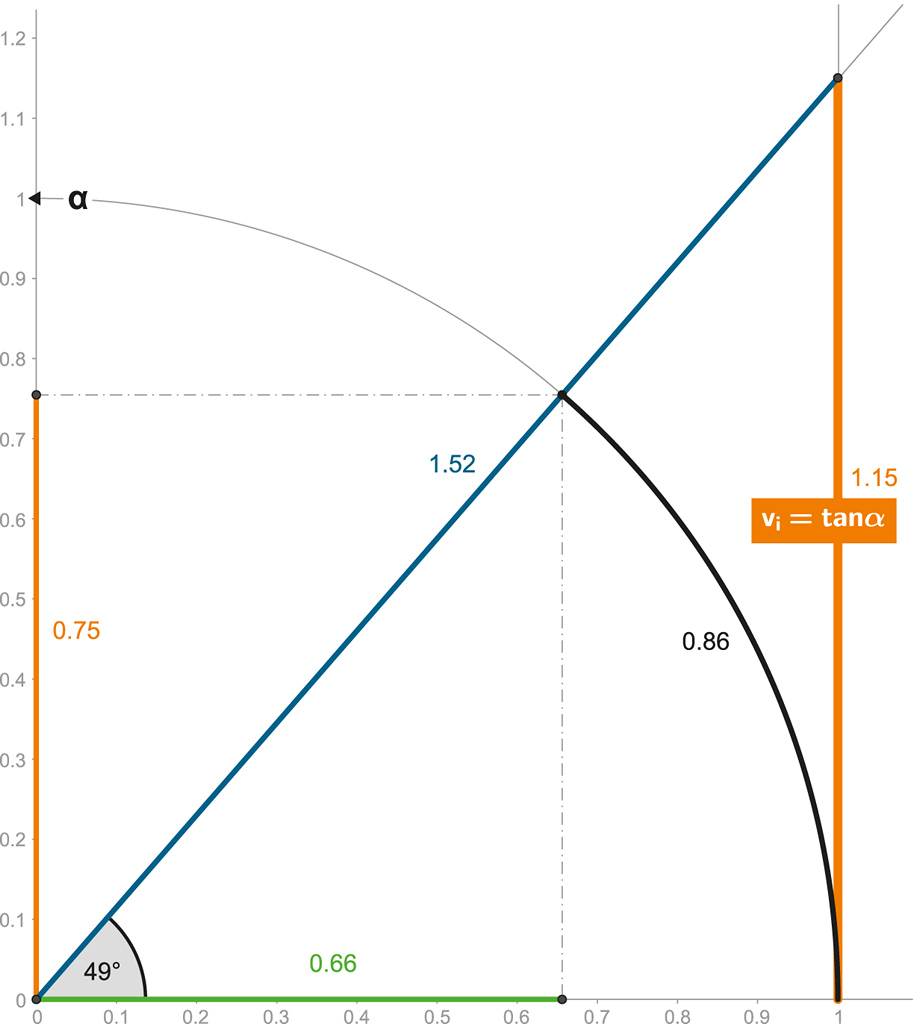
Obrázek 102:
Tangenta vyjadřuje rychlost pohybu měřenou z pozice interního účastníka.
Rychlost z pohledu interního uživatele je (oranžovou) tangentou časoprostorového úhlu, je číselně neomezená a limitně se blíží nekonečnu v situaci, kdy externí pozorovatel naměří „rychlost světla“ ve = c = 1.
vi = tan α
V našem vzorovém případě (dle obrázku) lze snadno spočítat (či odměřit na časoprostorové kružnici), že rychlost z pohledu interního účastníka je 1,15 (115 % c)!
Uvnitř časoprostorové kružnice můžeme spatřit několik pravoúhlých trojúhelníků – ve kterých samozřejmě platí Pythagorova věta. Díky ní lze hodnoty navzájem mezi sebou přepočítávat i bez trigonometrických funkcí (vystačíme si s druhými mocninami a odmocninami). Ve výsledku tudíž platí v jednotkové kružnici následující vztahy:
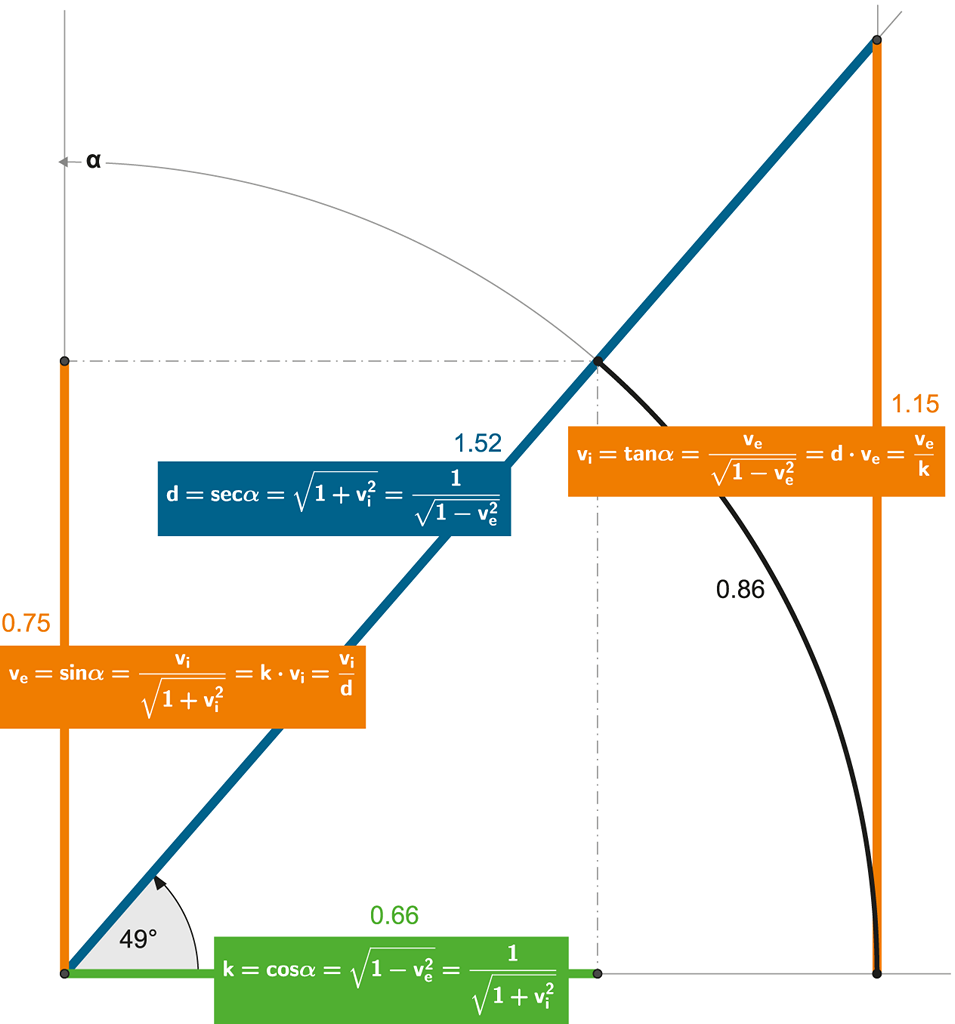
Obrázek 103:
Jednotková kružnice s kompletním matematickým aparátem.
α = časoprostorový úhel, roste s rychlostí pohybu. Při nulové rychlosti je nulový, při maximální rychlosti času (světla) je π/2 (90°).
Znovu připomínáme, že vyjadřujeme-li úhly (respektive délku kruhového oblouku, respektive „arc“) v radiánech – všechny poměry délek v diagramu (přímé linie i zakřivená délka kruhového oblouku) jsou proporcionální (viz Rozvoj trigonometrie). Ve fyzice a matematice jsou proto radiány nezbytností – nic jiného nedává smysl!
Úhel α označuje TČ jako tzv. časoprostorový úhel.
Úhel vyjadřuje poměr, respektive „mix“ délky (dráhy) a času (trvání) na celkovém pohybu v časoprostoru. Úhel vyjadřuje (alternativním způsobem) rychlost pohybu, respektive je „ručičkou tachometru“, která od horizontální 0° = 0 rad do vertikální polohy 90° = π/2 rad plynule postupuje od „klidu“ k „absolutnímu pohybu“.
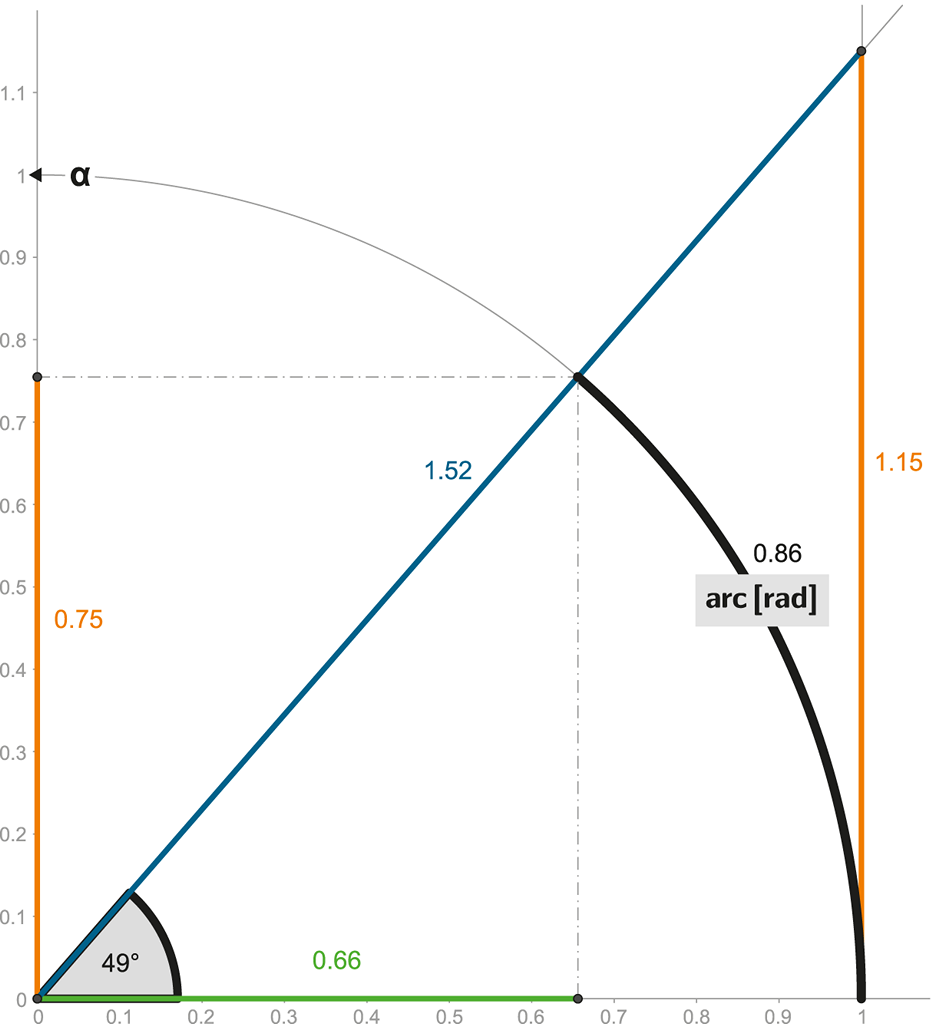
Obrázek 104:
Časoprostorový úhel 𝜶 je stěžejním údajem – pomocí trigonometrických funkcí nám snadno předá: externí rychlost, interní rychlost, kontrakce či dilatace času.
3.4.5.1 DILATACE/KONTRAKCE ČASU A ZMĚNA RYCHLOSTÍ
Ve smyslu výšeuvedeného je třeba přijmout skutečnost, že čas se v důsledku geometrie 4D časoprostoru jeví jinak pro externího a jinak pro interního pozorovatele:
Zatímco interní pozorovatel naměří kontrakci času (k) – konkrétní délkovou vzdálenost v prostoru urazí za kratší čas (nežli naměří externí pozorovatel); externí pozorovatel naměří dilataci času (d) – z jeho pohledu bude trvat pohyb po totožně dlouhé trajektorii delší dobu (nežli naměří interní účastník děje).
Efekt dilatace času způsobuje, že pozorujeme-li externě pohyb lineárně zrychlujícího objektu – postupem času (s rychlostí blížící se „světelným“ hodnotám) budeme pozorovat „zpomalování“ děje „zamrzajícího“ v čase – a s každým dalším přírůstkem rychlosti bude „zpomalený film“ čím dál pomalejší – a téměř se zastaví s tím, jak se pozorovaná rychlost bude limitně blížit rychlosti „světla“.
Perspektiva interního účastníka však bude zcela opačná – z jeho pohledu poběží jeho čas standardním tempem, rychlost bude růst lineárně a neomezeně – překročení rychlosti „světla“ nebude nic bránit – pozorované děje v externí soustavě však budou optikou interního účastníka stále zrychlovat.
Nemůže tomu býti jinak:
Rychlost není nic jiného nežli dráha/čas!
Ve výsledku způsobuje kontrakce času (optikou interního pozorovatele) navýšení rychlosti, respektive dilatace času způsobuje limitaci rychlosti!
Protože délkovou vzdálenost urazí interní účastník za kratší čas – musel mít (vůči měření externího pozorovatele) vyšší rychlost. Obrácenou optikou (externího pozorovatele) dilatace času způsobuje snížení rychlosti, jež je vždy taková, že pozorovaná rychlost nikdy nepřekročí rychlost „světla“!
si = se = s
ti ≠ te
vi ≠ ve
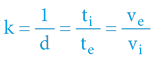
Bazální rovnice kinematiky v = s/t tím pádem zůstává v platnosti:
Jestliže nějaký objekt dorazil do cíle za kratší čas, musel mít proporcionálně vyšší rychlost – a totéž platí samozřejmě i v obrácené perspektivě.
3.4.5.2 UNIVERZÁLNOST DÉLEK
Časoprostorová kružnice i výšeuvedený odstavec objasňují, že délková vzdálenost je UNIVERZÁLNÍ!
Prostorová délka (metrové tyče či vesmírné vzdálenosti) je tatáž pro kohokoliv! Vzdálenosti ve vesmíru se nezkracují dle „relativního“ pohybu jednotlivých pozorovatelů (na rozdíl od TR).
Vzdálenost ze Země na Měsíc je stejná po každého! Stejně tak délkový etalon metru (uložený v Paříži) je stejně dlouhý pro kohokoliv – pro pařížského taxikáře, čínského kosmonauta kroužícího kolem Země i pro částice kosmického záření (pohybující se téměř rychlostí světla).
Délka není relativní veličinou, nýbrž je veličinou absolutní – univerzální!
3.4.5.3 POHYB MALÝMI RYCHLOSTMI
Je-li časoprostorový úhel α nulový, jde o „klid“ – nulovou změnu vzájemných délkových parametrů v prostorové rovině – nehybný předmět se v rámci časoprostoru pohybuje pouze v čase. Externí i interní pozorovatel sdílí „společný“ čas i délkové vzdálenosti – jsou shodně unášeni řekou času – naměří zcela stejné veličiny.
Dle tohoto scénáře fakticky probíhá i běžná realita našeho světa – neboť sebevětší rychlost lidským strojem dosažená je ve srovnání s rychlostí času (světla) de facto nulová – časoprostorový úhel (α) je při těchto „pozemských“ rychlostech tedy taktéž téměř nulový:
I v případě nejrychlejších dopravních prostředků lidstva – hodinky na naší ruce naměří „totéž“, co hodiny na letišti. A protože překonanou vzdálenost všichni urazí za „stejnou“ dobu, shodnou se i na „stejné“ rychlosti pohybu. Existující disproporce jsou běžně dostupnými technologiemi prakticky neměřitelné:
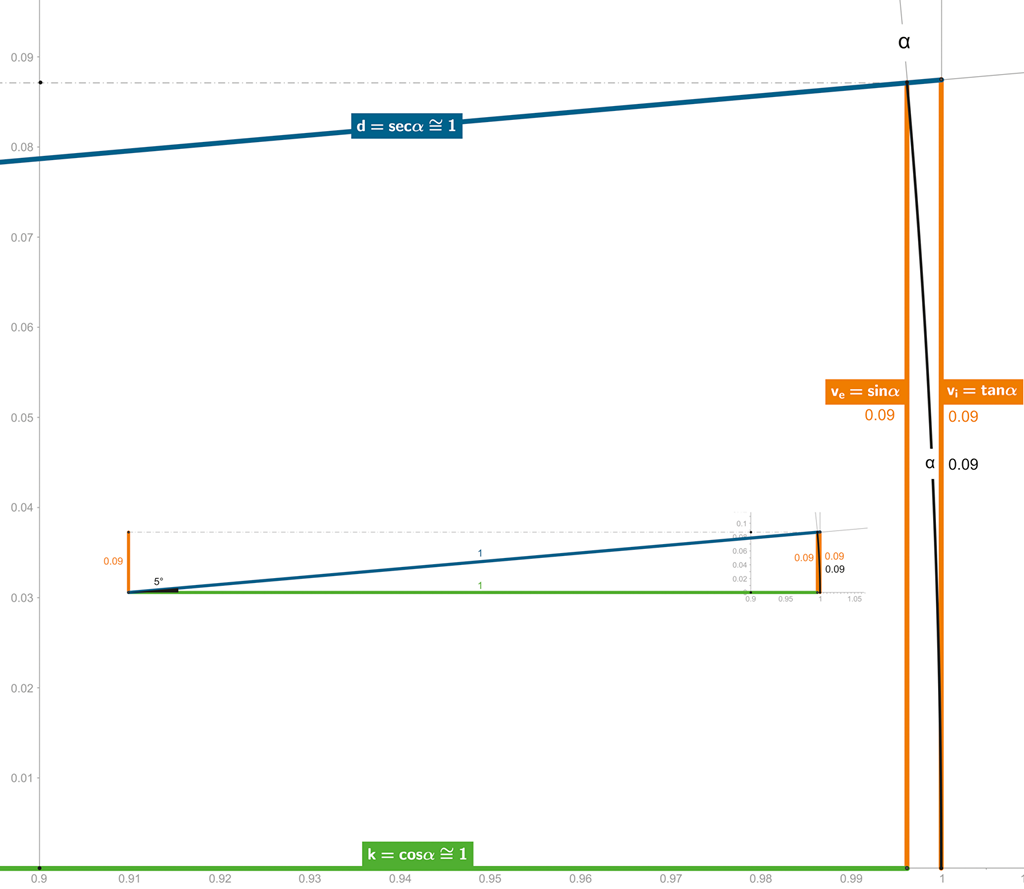
Obrázek 105:
Pro malé úhly je hodnota úhlu (arc), sinu i tangenty de facto totožná, neb cosinus i sekanta jsou (téměř) rovny jedné!
Pro malé úhly (do 0,09 rad ≈ cca 5°) je totiž hodnota sinus i tangens téměř totožná, respektive totožná radiánové hodnotě úhlu (arc); počítáme-li na 2 desetinná místa – sin, tan i arc jsou totožné; cos (vyjadřující kontrakci času) a sec (vyjadřující dilataci času) jsou rovny 1:
Úhel, jeho sinus i tangenta jsou tím více totožné, čím více se úhel limitně blíží nule! Spolu s tím se cosinus i sekanta limitně blíží jedné!
Při malém časoprostorovém úhlu je tudíž rychlost pohybu totožná pro externího i interního pozorovatele, analogicky tedy i naměřené časy:
Pozemní letištní stanoviště naměří letadlu Boeing rychlost 900 km/h = 250 m/s, což na naší jednotkové kružnici reprezentuje funkci sin α = ve = 0,0000008. Takovéto hodnotě sinu odpovídá prostorový úhel v hodnotě de facto totožné α = 0,0000008 radiánu (0,00005°). A pro takovýto úhel platí, že i hodnota tan α = vi = 0,0000008.
Z pohledu interního pasažéra proto bude na palubě letadla hodnota rychlosti totožná, jako naměří pozemský personál. Všichni se taktéž shodnou na časových údajích – neboť cosinus takto malého úhlu (kontrakce času z pozemské perspektivy) je téměř roven jedné, respektive cos α = k = ti/te = 0,9999999999996; a naopak – secans úhlu (dilatace času z pozice pasažéra) je analogicky neznatelně vyšší jedné sec α = d = te/ti = 1,0000000000004.
Pro podobně „malé“ rychlosti jsou tudíž sledované hodnoty jednotkové kružnice fakticky shodné – rozdíl bychom našli až v řádu 10‒13. Na palubě letadla proto nemáme šanci zaznamenat jakékoliv disproporce!
Nějaký další příklad?
Možná máte pocit, že vlastníte opravdu rychlý automobil a do sousedního města vzdáleného 21 km umíte díky své závodnické licenci dorazit za neuvěřitelných 500 vteřin (8:20 minuty). To je na pozemské poměry opravdu rychlé …
Za stejnou dobu však urazí čas (světlo) vzdálenost 150 milionů kilometrů, tedy vzdálenost ze Země ke Slunci! Vztyčíte-li v místě startu „virtuální“ kolmici směrem vzhůru až do vzdálenosti Slunce, pak můžete sestrojit imaginární trojúhelník s třetím vrcholem v sousedním městě (v cíli).
A protože je vámi absolvovaná vzdálenost naprosto „směšná“ v porovnání s délkou trajektorie, kterou za stejnou dobu urazí čas (světlo), výsledný trojúhelník má tak nicotný časoprostorový úhel, že přepona i přilehlá odvěsna takového trojúhelníku jsou de facto totožně dlouhé a tvoří „rovnoběžku“!
Onen zcela nepatrný poměr, o který je přepona tohoto trojúhelníku delší (nežli přilehlá odvěsna), je důvodem, proč stejně nepatrný je i poměr dilatace času při vaší „rychlé“ jízdě:
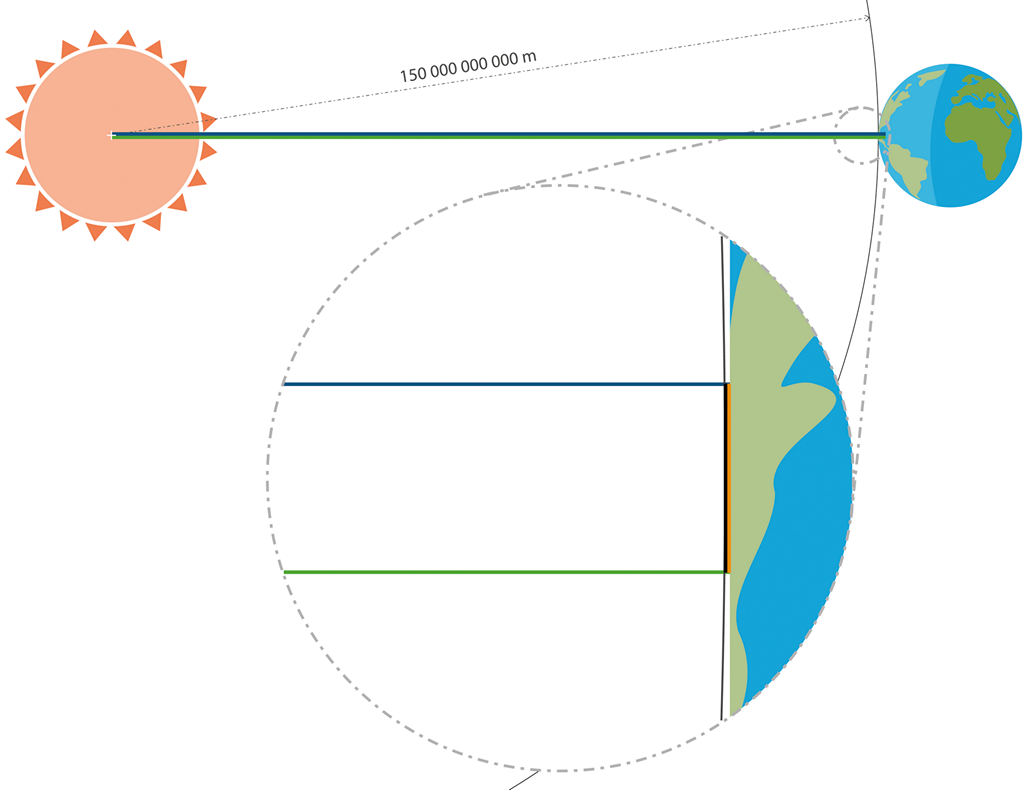
Obrázek 106:
Malá rychlost = malý úhel = „nulové“ (neměřitelné) časové či rychlostní disproporce.
Pouze s použitím sofistikovaných (a drahých) technologií nalézáme v pozemských poměrech reálné důkazy potvrzující matematiku 4D časoprostoru (matematiku Pythagora, respektive Minkowského):
Moderní experimenty s reálnými makroskopickými objekty – atomové hodiny na orbitách planety Země, na palubách letadel či v pozemských laboratořích – prokazují „fungování“ jednotkové kružnice, ale opět pouze na velmi malých časoprostorových úhlech – kde výsledky experimentů sice generují reálné časové disproporce, avšak jen ve velmi malých řádech a s použitím drahých technologií.
3.4.5.4 POHYB VELKÝMI RYCHLOSTMI
Výrazný efekt matematiky jednotkové kružnice (pravoúhlého trojúhelníku) se projeví teprve u pohybů velkými rychlostmi – řádově srovnatelnými s rychlostmi času (světla):
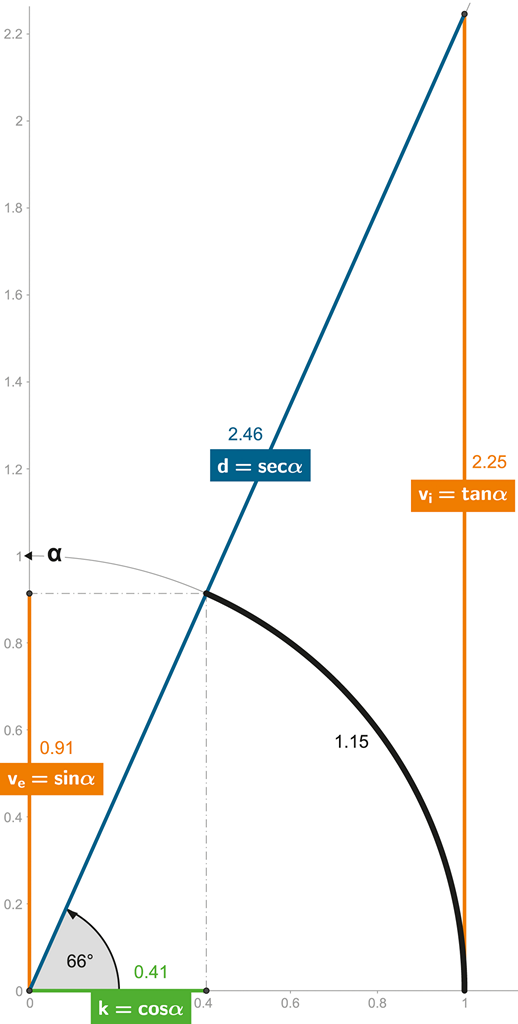
Obrázek 107:
Pro větší úhly se již hodnoty trigonometrických funkcí liší diametrálně – sinus je menší nežli úhel (arc), tangenta je naopak větší!
V našem pozemském světě můžeme zřetelné (zjevné) důkazy existence 4D prostoru zaznamenat pouze v částicové fyzice. Experimenty s miony v pozemské atmosféře či s různými druhy částic v urychlovačích umožňují externě pozorovat hmotné objekty, které se prostorem pohybují s nejrůznějšími prostorovými úhly, někdy i téměř π/2 radiánu (90°)!
V těchto situacích jsou již siny, cosiny i tangenty úhlu zcela rozdílné – disproporce v rozdílném toku času jsou exaktně pozorovatelné – v souladu s uvedenými matematickými vztahy pravoúhlého trojúhelníku (jednotkové kružnice).
3.4.5.5 POHYB RYCHLOSTÍ ČASU
Je-li časoprostorový úhel (α) maximální (π/2, respektive 90°), jde o limitní pohyb – objekt se pohybuje (maximální) rychlostí spolu s časem, a protože v takovém případě objekt „dohnal“ čas – pohyb se v rámci časoprostoru již celý odehrává pouze v jeho délkové složce, časová složka je nulová!
Tento scénář však zůstává lidstvu nedostižně vzdálen. Teprve až ovládneme technologii ze seriálu Star Trek a budeme se moci transformovat do paprsku světla (jde samozřejmě o nadsázku) – pak budeme moci prostorem cestovat za nulový čas – „okamžitě“ se budeme moci přesunout na druhý konec vesmíru.
Zatímco externí pozemští pozorovatelé budou sledovat let našeho paprsku (jejich externí optikou poletíme rychlostí světla) do vzdálenosti milionů světelných let (miliony let se budou střídat nové a nové generace vědců na observatoři), my nestihneme „na palubě“ transportního paprsku ani mrknout a budeme v cíli. Čas našeho letu bude nulový. Rychlost z našeho pohledu bude nekonečná stejně tak, jako je nekonečná tangenta pravého úhlu!
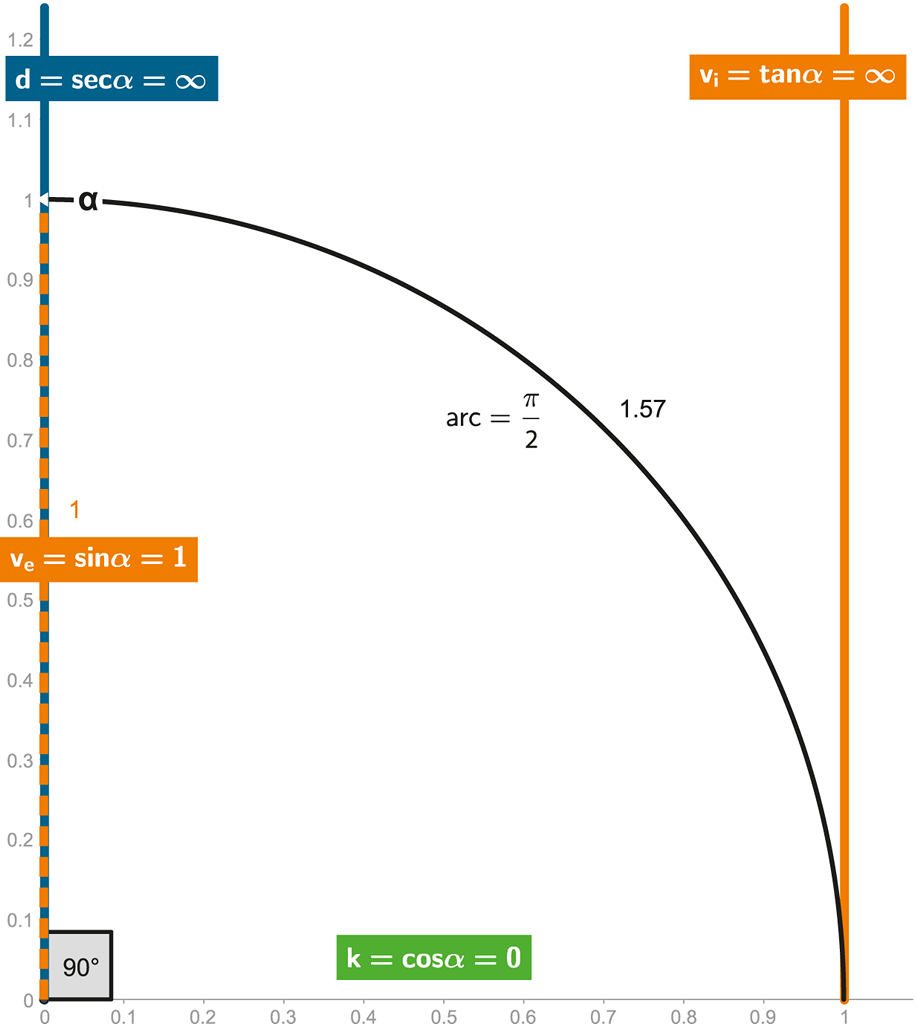
Obrázek 108 + ANIMACE:
Za této situace se externí rychlost jeví jako „rychlost světla“, interní rychlost je nekonečná!
Vědci i obyčejní lidé si občas kladou otázku: Proč je rychlost světla taková, jaká je?
Nemá však smysl hledat v hodnotě rychlosti světla (času) nějaký „vyšší“ skrytý význam, tajemnou hádanku či poselství prozřetelnosti:
Hodnota rychlosti světla c = 299 792 458 m/s pouze odráží, jak nešikovně si lidé kdysi zvolili měřítko pro sekundu a pro metr. Perioda rotace naší planety (od níž je sekunda původně odvozena) nemá žádný příčinný vztah k velikosti planety (metr byl původně definován jako deseti milióntina zemského kvadrantu).
Z pohledu TČ je odpověď snadná:
Rychlost času (světla) je 1! Tak to vždy bylo, je a bude – v celém vesmíru. Je to ona magická, úžasná a veledůležitá jednička!
3.4.5.6 4D SVĚT V PRAXI
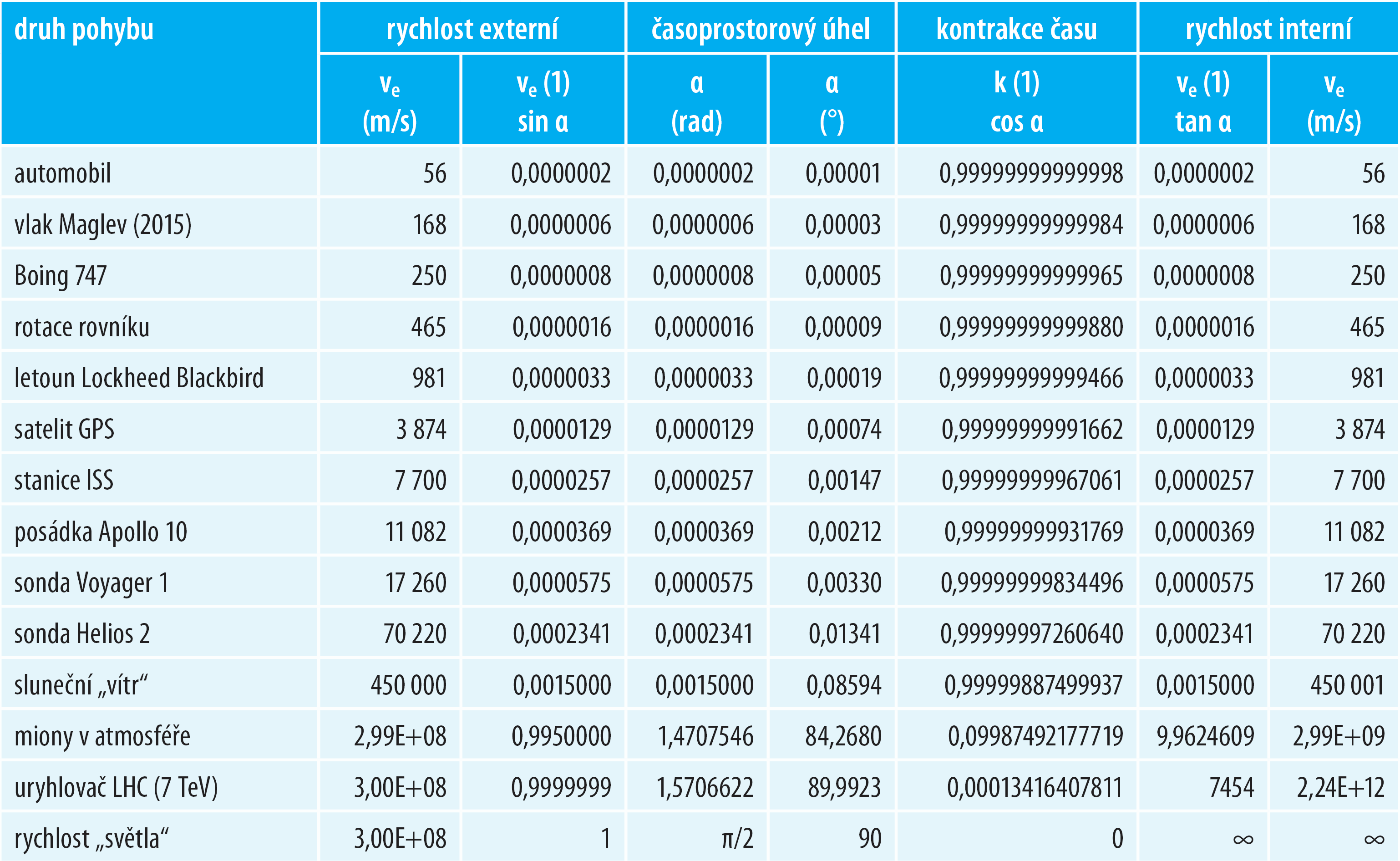
Tabulka 4: Efekt 4D časoprostoru pro pozemské i nadpozemské rychlosti
Náš životní „prostor“ je dualitou délkových a časových vzdáleností – vše existuje a vše se odehrává v „bipolárním“ časoprostoru. Dokonce i onen slovní pojem „prostor“ má (a vždy historicky měl) svůj časový význam: V hektické době často hledáme „časový prostor“!
Zvykejme si tedy postupně na to, že není nutné používat termín „časoprostor“ či „prostoročas“ – slovo „prostor“ je dostatečně duální – má svůj délkový i časový kontext.
Dualita je častým jevem moderní fyziky:
Elektřina je duální – má svou elektrickou i magnetickou povahu, respektive elektromagnetické projevy. Samotné elektromagnetické záření (včetně světla) je taktéž duální – projevuje se částicově (fotony) i jako vlnění.
Stejně tak si zvykněme na dualitu prostoru – každý fyzikální děj se odehrává v konkrétním čase (měříme sekundami) a v konkrétní délkové trajektorii (taktéž měříme sekundami)! Nejde o dvě svébytné kategorie – jde o jednu jedinou!
Časoprostor existuje stejně samozřejmě jako elektromagnetismus – teprve spojení obou kategorií dává fyzikální smysl každé z nich! Ve chvíli, kdy začneme i délku měřit sekundami, pochopíme velikost odkazu Hermanna Minkowského a dilatace/kontrakce času pro nás přestanou být záhadou či fantaskním výmyslem sci-fi tvůrců.
Dualita 4D prostoru je jediný postulát TČ, v jehož přímém důsledku je snadné objasnit dilataci/kontrakci času, změnu rychlostí i zdánlivou „omezenost“ rychlosti šíření hmoty a informace prostorem.
Plně postačuje bazální matematika (Pythagorova věta) a trocha představivosti (plavec v řece). Znalost trigonometrických funkcí (v jednotkové kružnici) je nicméně značnou výhodou.
Všimněme si toho, že ať již se objekt pohybuje v časoprostoru pod jakýmkoliv časoprostorovým úhlem (kdekoliv po obvodu jednotkové kružnice), vždy se objekt v prostoru vzdálí o stejnou vzdálenost – vždy o jednu sekundu:
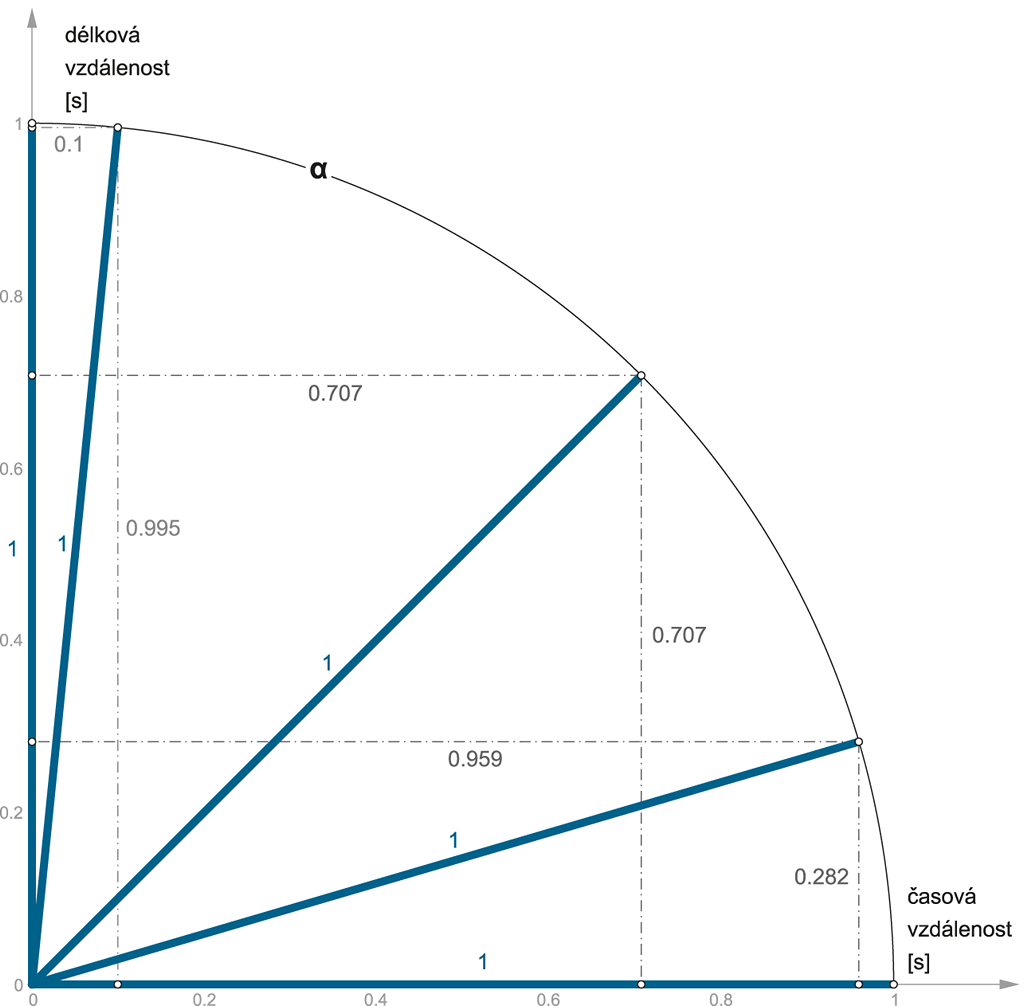
Obrázek 109:
Celková „bipolární“ vzdálenost je VŽDY 1 sekunda!
• Sekunda nehybného objektu bude celá tvořena pouze časovou složkou prostoru (prostorová složka bude nulová).
• Sekunda na palubě Boeingu bude velmi podobná předchozímu scénáři, rozdíl bude měřitelný pouze atomovými hodinami.
• Sekunda paprsku světla bude naopak celá pouze sekundou prostorovou (interní čas paprsku světla bude nulový).
• Sekunda mionu bude z 99,5 % tvořena prostorovou složkou a jen z 10 % časovou složkou: 0,9952 + 0,12 = 0,99 + 0,01 = 1
Vše ve vesmíru se neustále pohybuje prostorem!
Rozdíl je jen v „mixu“ obou prostorových složek. Všichni se neustále pohybujeme v (časo)prostoru – byť valnou většinou pouze v jeho časové složce!

