DIFERENCIÁLNÍ MATEMATIKA
Newton s Leibnizem (nezávisle na sobě) vynalezli diferenciální počty – derivace, integrály, diferenciální rovnice. Je dobré připomenout, že Newton fakticky navázal na svého učitele Isaaca Barrowa, který je objektivně faktickým „vynálezcem“ derivace v matematice (byť základy znal již Galileo). Barrow jako první derivoval matematickou funkci – údajně na zakázku vojenské generality, ve snaze spočítat tečnu dráhy dělostřelecké koule.
Byť současné názvosloví této oblasti matematiky pochází od Leibnize, použil Newton diferenciální matematický aparát jako první ve službách fyziky – při tvorbě svých zákonů gravitace a objasnění tíhového zrychlení Země.
Přestože ve školách patří tato část matematiky spíše mezi „neoblíbené“ oblasti, neuškodí připomenout si její velkolepý praktický význam:
1.29.1 INTEGRÁL
I když se v hodinách matematiky může zdát výpočet integrálů samoúčelný – význam integrálů pro fyziku i technické vědy je zcela zásadní!
V matematice, geometrii, fyzice, stavebnictví a mnoha dalších oborech je často potřeba spočítat plochu „pod křivkou“.
Nakreslíme-li například graf pohybu tělesa, kdy na jedné ose vyneseme rychlost a na druhé čas, plocha pod křivkou je celkovou dráhou, kterou těleso urazilo. Onen vztah z hodin fyziky s = v · t totiž platí jen pro rovnoměrný pohyb. Výpočet dráhy obecného pohybu tělesa je totiž možné určit právě a jen integrálním počtem, kdy platí, že s = ∫v dt, respektive:
Dráha se rovná ploše pod křivkou rychlosti (v závislosti na čase).
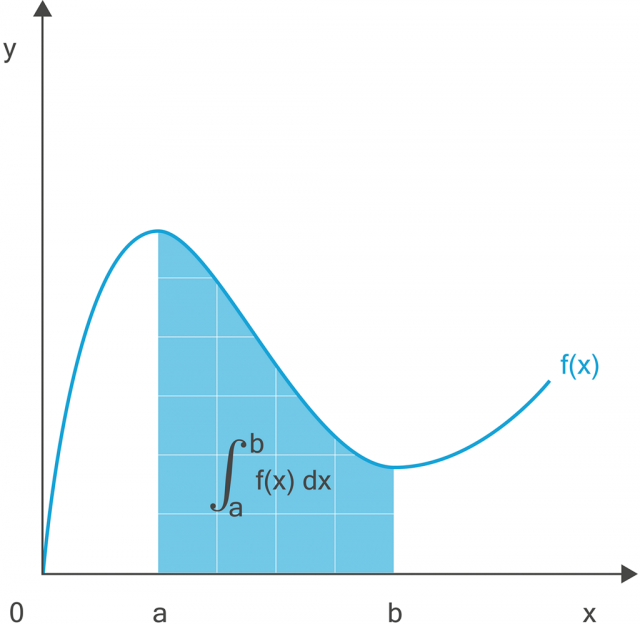
Obrázek 33:
Integrál exaktně „sčítá“ fyzikální veličiny. V grafickém vyjádření představuje plochu pod křivkou dané funkce.
Analogicky známe z hodin fyziky vztah pro výpočet energie práce E = F · s.
Působíme-li na těleso silou po určité dráze, spotřebujeme k tomuto úkonu energii (práci) rovnou součinu síly a dráhy. Tento jednoduchý vztah opět platí jen pro konstantní velikost síly a pro obecné působení síly je třeba vztah transformovat pomocí integrálů na E = ∫ F ds.
Energie se rovná ploše pod křivkou síly (v závislosti na dráze).
Rakety létající do vesmíru létají úspěšně mimo jiné i díky integrálnímu počtu. Hmotnost rakety během letu klesá (s tím, jak se spotřebovává palivo), stejně tak gravitační síla Země je menší ve větších výškách. Mnoho dalších faktorů se mění v závislosti na času i dráze letu. Integrální počet dovoluje všechny tyto měnící se faktory zahrnout do přesných výpočtů a úspěšně splnit letový plán.
1.29.2 DERIVACE
Derivace je inverzní funkcí k integrálům a geometricky vyjadřuje tečnu ke křivce.
Vyneseme-li do grafu pohybujícího se tělesa závislost dráhy na čase, pak tečna křivky v každém jejím místě určuje rychlost v = ds/dt. Vztah opět známe spíše v jeho zjednodušené podobě pro rovnoměrný pohyb v = s/t.
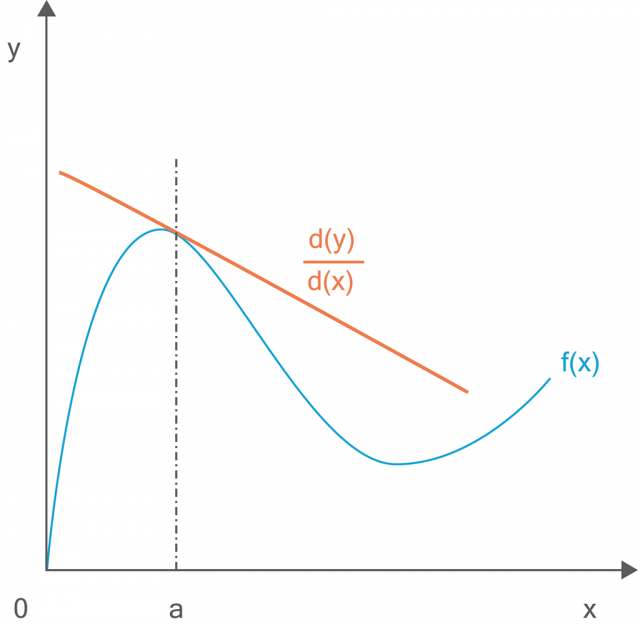
Obrázek 34:
Derivace je opakem integrálu, vyjadřuje míru růstu či poklesu dané funkce. V grafickém vyjádření představuje tečnu k dané křivce.
Derivace nám tedy umožňují provést opačný postup nežli integrály:
Známe-li například průběh dráhy (vzdálenosti) v čase, získáme první derivací rychlost a následnou druhou derivací zrychlení.
Integrály a derivace jsou nerozluční spojenci na cestě k exaktnímu poznání většiny vědeckých oborů. Za objevení této oblasti matematiky vděčíme především Newtonovi a Leibnizovi – oba objevili tyto počty nezávisle na sobě – oběma patří náš obdiv.

