SOUVISLOSTI STR A OTR
Teoretickým fundamentem výšeuvedené matematiky TR v oblasti gravitace je (v minulých kapitolách již zmíněné) Schwarzschildovo řešení Einsteinových rovnic, jež finálně vedou ke stěžejnímu vztahu OTR:
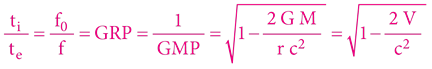
V našem (předchozím vzorovém) scénáři (externí pozorovatel na okraji Sluneční soustavy pozoruje sluneční záření) vyjadřuje vzorec následující:
tetrvání děje z pohledu externího pozorovatele na okraji SS
titrvání děje z pohledu interního účastníka „pádu“ v gravitačním poli Slunce
ffrekvence záření při dopadu na povrch Slunce
f0frekvence světla při jeho vzniku na okraji SS
Ggravitační konstanta (6,67·10‒11 N·m2·kg–2)
Mhmotnost Slunce
rpoloměr Slunce
crychlost světla
Vkladný gravitační potenciál ve vzdálenosti r (V = GM/r)
GRPgravitační rudý posuv
GMPgravitační modrý posuv
Geniální matematik Karl Schwarzschild dospěl k výšeuvedenému vztahu na základě poměrně komplikovaného řešení diferenciálních rovnic OTR.
Ke zcela totožnému „Schwarzschildovu řešení“ však může dojít každý čtenář této knihy zcela triviální substitucí dvou bazálních vztahů!
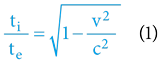

První vzorec je „klasickým“ vztahem pro přepočet pohybové dilatace/kontrakce času, ať již dle TR či TČ – v otázce časových disproporcí se obě teorie (a matematické vztahy) shodují (byť TR vše vnímá „relativisticky“ tak, že si vzájemné časové disproporce protiřečí).
Druhý vztah je „obyčejným“ newtonovským vzorcem pro výpočet 2. kosmické rychlosti – kvantifikuje minimální únikovou rychlost z povrchu nebeského tělesa pro překonání gravitace, respektive (obrácenou perspektivou) jde o dopadovou rychlost na povrch nebeského tělesa, padá-li objekt z nekonečné (hodně veliké) vzdálenosti.
Dosadíme-li substitucí druhý vztah do prvního vztahu v = v2, výsledkem je Schwarzschildovo řešení:

Určit vztah pro výpočet kritického „Schwarzschildova poloměru“ (minimální poloměr pro vznik „Černé díry“) je opět triviální: Hledáme poloměr, při kterém je 2. kosmická rychlost rovna rychlosti světla (c):
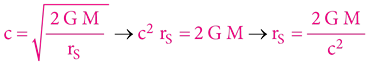
Na základě posledního vztahu hravě ověříme, že Schwarzschildův poloměr našeho Slunce je cca 2955 metru.
V jediném substitučním kroku jsme společně odvodili vztah (3), který je nejdůležitějším fyzikálním vzorcem OTR v oblasti gravitace! Právě tento matematický vztah hraje hlavní roli při mnoha „důkazech“ platnosti TR, ať již jde o GRP, matematiku „Černých děr“ i matematický aparát satelitních navigačních systémů.
Primárně nám však výšeuvedené matematické odvození (3) pomůže pochopit sci-fi příběh, který nám TR vypráví o gravitaci a čase:
Upustíme-li v daleké vzdálenosti od masivního nebeského tělesa „pípající“ sondu, silná gravitace (jež působí do nekonečna) bude sondu pozvolna přitahovat a sonda započne „padat“ k onomu hmotnému obru. Rychlost pohybu padající sondy se bude řídit prastarými newtonovskými zákony (v závislosti na gravitačním potenciálu).
STR však již v roce 1905 objasnila, že rychlost pohybu jakéhokoliv hmotného objektu nemůže růst do nekonečna, nýbrž se může pouze limitně přiblížit rychlosti světla, která je konečná (c = 299 792 458 m/s). Stejná STR taktéž popsala dilataci času – s rostoucí rychlostí se veškeré děje pohybujícího se objektu jeví externímu pozorovateli jako zpomalující a čas zcela „zamrzá“ s limitní rychlostí světla.
A protože gravitace je jev, při kterém objety zrychlují pádem do silnějšího gravitačního pole – vzrůstající rychlost pádu v gravitačním poli znamená zpomalování dějů během pádu v silnějším gravitačním poli – v souladu s principem vyšší dilatace času při vyšší rychlosti (STR).
Externě (z místa vypuštění, kde je gravitační potenciál de facto nulový) pozorované pípání naší imaginární sondy bude tudíž zpomalovat spolu s tím, jak bude růst rychlost jejího pádu – dle matematiky STR pro pohybovou dilataci času! V důsledku zpomalování času bude úměrně klesat zrychlování sondy s tím, jak se její rychlost bude limitně blížit rychlosti světla.
Interval pípání sondy bude zpomalovat shodnou měrou, jakou bude klesat i vlastní frekvence vysílaného signálu – příčinou všech těchto jevů totiž bude pohybová dilatace času!
Na palubě samotné sondy se nic nestandardního dít nebude – všechny palubní chronometry budou fungovat řádně – při interakci se základnou (v místě vypuštění, kde je gravitační potenciál de facto nulový) se však veškeré děje na základně budou (naopak) jevit zrychlené!
Všimněme si pozorně, že právě tímto tvrzením začíná Teorie relativity popírat princip relativity!
Jakmile sonda dosáhne (interně) rychlosti světla – překoná Schwarzschildův poloměr, respektive „horizont událostí“ – před „očima“ sondy (či interních kamer) probleskne veškerá budoucnost vesmíru a pak … nikdo netuší, co je „pak“ … situace nemá fyzikální interpretaci … zbývají již jen nepodložené hypotézy a sci-fi bláboly o „vlastnostech“ Černých děr.
Souhrnný vztah gravitace a času dle TR:
• S růstem gravitačního potenciálu roste rychlost volného pádu, a to „klasicky“ (dle newtonovské fyziky) …
• S rostoucí rychlostí volného pádu se zpomaluje čas (dle STR).
• S růstem gravitačního potenciálu tudíž zpomaluje čas (OTR)!
• S poklesem gravitačního potenciálu tudíž čas zrychluje (OTR)!
A právě takovýto princip je fundamentem OTR – právě tento „mechanismus“ je obsažen ve stěžejním matematickém vztahu TR ke gravitaci. Uvědomit si výšeuvedené – je naprosto zásadní!
OTR (která též bývá nazývána „Teorií gravitace“) nám totiž o gravitaci sdělila fakticky jediné, a to:
• V silnějším gravitačním poli plyne čas pomaleji …
• Tato gravitační dilatace času (dle OTR) je tatáž jako pohybová dilatace času (dle STR) pro 2. kosmickou rychlost (na základě newtonovských vztahů).
Neboli:
Gravitační dilatace času (dle OTR) je rovna pohybové dilataci času (dle STR) při „únikové“ rychlosti, která zajistí objektu trvalé opuštění gravitačního pole nebeského tělesa z dané úrovně gravitačního potenciálu.
Neboli:
Gravitační dilatace času (dle OTR) je rovna pohybové dilataci času (dle STR) při rychlosti volného pádu „z nekonečna“ do dané úrovně gravitačního potenciálu.
Právě takováto tvrzení jsou fundamentem TR!
Bylo nutné je odhalit a obnažit (zahalené do relativistického hávu nepřehledných matematických konstrukcí), abychom je následně mohli zpochybnit:

