EUKLIDES
„Prostor je nekonečný co do rozlohy, není však donekonečna dělitelný.“
Euklides
Euklides patří zaslouženě mezi největší učence starověku. Místo i datum jeho narození (jakož i velká část jeho života) jsou poněkud nejasné, nicméně jeho dílo lze datovat cca okolo roku 300 př. n. l.
Euklides bývá označován za Platónova žáka, studoval v Athénách na Platónově akademii. Později byl Euklides povolán do nově založené Alexandrijské knihovny.
Aristoteles, Archimedes, Eratosthenes i Alexandr Veliký byli současníky Euklida, Archimedes byl údajně i jeho žákem. Euklides se věnoval především matematice a geometrii, přičemž jeho dílo lze dodnes považovat za fundamentální základy matematiky a prostorových vlastností našeho světa.
Euklidovy Základy jsou i dnes hojně užívány při studiu matematiky a patří (spolu s Biblí) mezi historicky nejpublikovanější knihy světa! Dílo sestává z 13 knih, v nichž Euklides shrnul a systematizoval dobové znalosti matematiky a geometrie – zahrnující základní geometrické definice; matematiku kruhu, trojúhelníku i víceúhelníku; teorii čísel i problematiku výpočtu povrchů a objemů těles.
S ohledem na tematiku této knihy je třeba vyzdvihnout především desítku úvodních postulátů Základů, jež říkají:
• Bod je to, co nemá části.
• Úsečka je délka bez šířky.
• Každými dvěma body lze vést úsečku.
• Tuto úsečku lze libovolně prodloužit.
• Konce úsečky jsou body.
• Každou úsečkou lze opsat kružnici kolem jednoho jejího konce.
• Mějme přímku a bod. Tímto bodem lze vést jen jednu rovnoběžku s danou přímkou.
• Všechny pravé úhly jsou si rovny.
• Věci rovné jedné a téže věci jsou rovné i sobě navzájem.
• Když se k rovným přidá stejné, jsou i součty stejné.
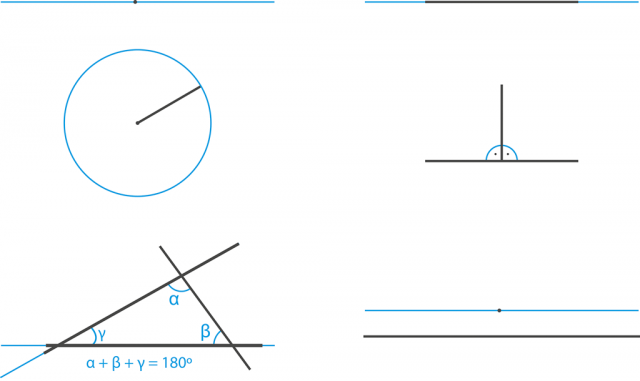
Obrázek 6:
Svými „Základy“ Euklides položil základy.
Nakolik se mohou některé uvedené definice dnes zdát triviální – jsou Základy první syntetickou vědeckou prací, kde na základě úvodních jednoduchých definic bylo v následujících knihách odvozeno téměř veškeré matematické vědění starověku.
Především však Euklides definoval některé „pravdy“, které dodnes všichni používáme v geometrických a prostorových úvahách nad naším světem: Trojúhelník má vždy celkem 180°, rovnoběžky se nikdy neprotínají a v pravoúhlém trojúhelníku vždy platí Pythagorova věta.
Polohu bodu v ploše konstruujeme vždy na základě dvou vůči sobě kolmých souřadnicových os, v případě 3D prostoru pak používáme systém 3 vzájemně kolmých os. A přestože podobným konstrukcím dnes říkáme Kartézský graf (viz René Descartes, o cca 2 tisíce let později), fundamentální základ pro chápání geometrických vlastností prostoru položil pro všechny své následovníky právě Euklides.
V tomto ohledu se vžilo označení Euklidův prostor – vyjadřující svět, v němž lze veškeré dynamické jevy zapisovat formou vzájemně kolmých souřadnic (2 souřadnice pro 2D prostor, 3 souřadnice pro 3D prostor atd.)
V Euklidově prostoru se odehrává vše – mapují se světadíly či hvězdná obloha, zapisují se údaje o trajektorii vesmírných letů i GPS souřadnice dopravních letadel … Euklidův prostor popisuje svět, v němž žijeme!

