CESTOVÁNÍ KE HVĚZDÁM DLE TR

Již z předchozích kapitol je zřejmé, že Einstein měl „problematický“ vztah k myšlence Minkowského 4D prostoru – kterou na pár let nejprve zavrhnul (v kontext STR) a následně ji (pokřivenou Riemannovskou geometrií) naopak činní základem své OTR.

Existuje mnoho indicií, že TR hloubku Minkowského myšlenek nikdy korektně neuchopila, což vede ve výsledku k mnoha nekorektním matematickým vzorcům a absurdním předpovědím TR. Markantním příkladem je i problematika „cestování ke hvězdám“:

Lidstvo vždy zajímala otázka, jak hluboko do vesmíru bude moci jednou proniknout, až naše technologická úroveň nabídne efektivnější způsoby pohonu, nežli je současný (málo produktivní) způsob uvolňování energie z chemických vazeb hořících sloučenin.

Jedinými omezeními v plánování vesmírných výprav pak zůstane pouze omezená délka lidského života a chatrná tělesná schránka člověka, která dlouhodobě nesnese vyšší přetížení (zrychlení). Jak daleko do vesmíru lze s těmito omezeními cestovat?

Relativisté mají k této problematice vytvořený teoretický scénář i příslušné matematické řešení:

Scénář spočívá v konstantním zrychlování kosmické lodi v první půlce letu, následuje konstantní zpomalování v druhé půli letu. Ideálně bývá uvažováno se zrychlením/zpomalením v hodnotě pozemského tíhového zrychlení (10 m/s²), které na palubě lodi vytvoří de facto pozemskou gravitaci, a lidský organismus tak nebude během letu strádat (na rozdíl od kosmonautů v beztížném stavu na zemské orbitě). Bude to praktické – situace na lodi (včetně tíhy předmětů a lidí) bude zcela „pozemská“.

Matematické řešení této úlohy je principiálně poměrně snadné – díky Newtonovi s Leibnizem a jimi objevenému integrálnímu počtu, který principálně souhrnně spočítá časové disproporce (dle dilatace času) pro všechny úseky letu (na startu při malých rychlostech jsou disproporce zanedbatelné, s postupným zrychlováním lodi rostou).

Ponechme nyní stranou poněkud naivní představu výšeuvedeného scénáře – v reálném vesmíru totiž lze ke zrychlování (i zpomalování a změně směru) využít hmotné objekty poblíž trajektorie letu (tzv. gravitační manévry) – diskutováno v kapitole Paradox dvojčat, a to vše bez jakýchkoliv silových účinků na vesmírnou loď či její posádku. Navržený scénář tedy berme spíše jako „teoretickou úlohu“ a soustřeďme se na kvantitativní a principiální „problémy“ této části TR:

2.13.1 OPTIMISTICKÝ PARADOX

Co se kvantitativního aspektu týče, existuje-li dilatace času – je třeba při integrování zvolit ten „správný“ čas a ke správné volbě je třeba správně uchopit Minkowského časoprostor. Problematika bude více diskutována v následujících kapitolách (viz Cestování ke hvězdám). Na tomto místě pouze zmíníme příliš „fantaskní“ předpovědi TR:

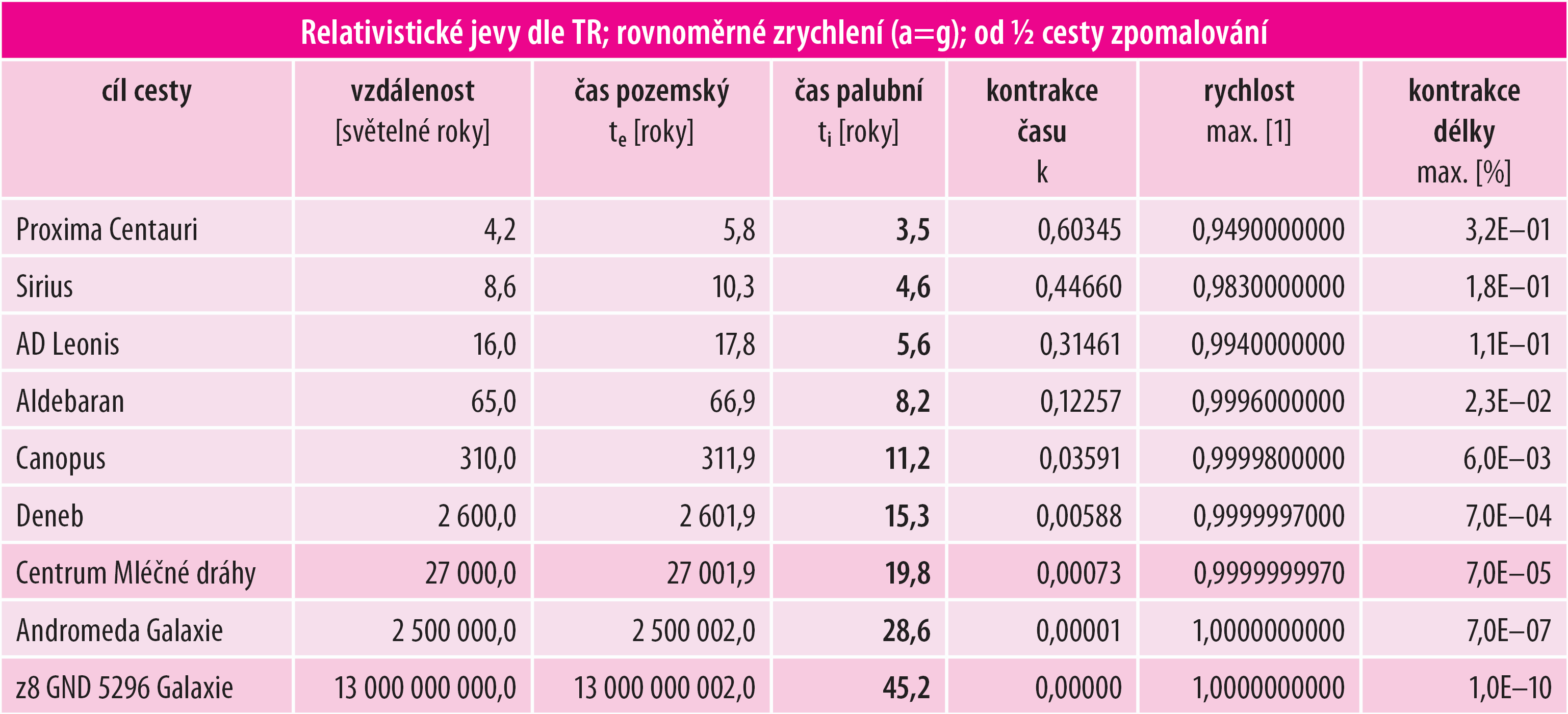
Tabulka 2: Optimistický scénář dle TR

Matematické vztahy odvozené na základě TR tvrdí, že běžným pozemským zrychlením/zpomalením lze za 20 let doletět do centra naší Mléčné dráhy vzdálené cca 27 tisíc světelných let! Maximální rychlost letu bude 99,9999997 % rychlosti světla, a to vše díky tomu, že vesmír (vzdálenost k cíli) se kosmické lodi zkrátí (díky kontrakci délek) v nejrychlejší části letu na pouhých 0,007 % původní vzdálenosti. Na Zemi mezitím uběhne 27 002 tisíc let! Nezdají se taková čísla poněkud příliš optimistická?

Pakliže nikoliv, tak dodejme, že za cca dvojnásobnou dobu – za 45 let – lze dle TR „pohodlně“ doletět až na nejzazší konec vesmíru, tedy do vzdálenosti 13 miliard světelných let! Celý let budou pozemšťané pozorovat (po generacích) následujících taktéž 13 miliard let!

Skvělá bilance pro scénáristy hollywoodských sci-fi filmů … ale pro vědce?

2.13.2 SYMETRICKÝ PARADOX

Závažnějším (principiálním) problémem je však … princip relativity. Ano, opět!

V kapitole Paradox dvojčat je podrobně diskutován argument TR, že ke skutečnému paradoxu dvojčat nemůže docházet proto, že scénář není „symetrický“. TR argumentuje, že princip relativity samozřejmě platí univerzálně (Země obíhá kolem Slunce, Slunce obíhá kolem Země), ale při scénáři mezihvězdných letů vnikají na straně mimozemského dvojčete silová působení (během zrychlování, zpomalování či otáčení směru letu), která narušují stavovou symetrii obou dvojčat (pozemské dvojče je „v klidu“). Výšeuvedený scénář mezihvězdných letů však staví TR před další „nepříjemnou“ konfrontaci:

Při scénáři vesmírné expedice dle minulé kapitoly totiž k žádnému porušení symetrie nedochází! Je-li let plánován se zrychlováním/zpomalováním v hodnotě pozemského zrychlení g ≅ 10 m/s2, je výšeuvedený scénář naprosto „symetrický“. Však právě proto je tak navržen – aby dlouhodobá silová působení na lidský organismus byla totožná pozemské gravitaci!

Stěžejním postulátem STR je princip ekvivalence – gravitační síly a setrvačné síly jsou rovnocenné. Silová působení (ať již na přístroje, či posádku) na kosmické lodi či v pozemském simulátoru proto budou (při uvažovaném scénáři) zcela identická! Rozespalý kosmonaut si nebude po probuzení jistý, zda je ještě v pozemském simulátoru, anebo je již ve vesmíru – bude jen jediná síla – velikostně totožná s pozemskou tíhou!

Na jednu stranu tak TR říká, že za 40 let lze doletět do centra Mléčné dráhy a zpět, zatímco na Zemi uplyne 54 tisíc let!

Její princip relativity však stejně tak postuluje, že je tomu zároveň i přesně obráceně – na cestu do vesmíru a zpět se vydala planeta Země, a tudíž pozemšťanům uplyne pouze 40 let, zatímco kosmonauti budou celý let zeměkoule pozorovat po dobu 54 tisíc let!

Paradox dvojčat je tak opět na scéně a pro TR před ním není úniku. Kdo tedy bude po návratu starší?

Jedni? Druzí?? Všichni???

Diagnóza TR je nevyléčitelná – je systémová!