ZÁKLADNÍ DEFINICE
Abychom si v následující části knihy lépe porozuměli, ujasníme si terminologii, která bude nadále v rámci TČ používána. Mnohé veličiny a jednotky je třeba si pouze připomenout, jiné nově definovat – aby byly smysluplnější. Vše v zájmu vyšší exaktnosti a mimo jiné i zjednodušení fyzikální interpretace a následných matematických vzorců.
Poznámka:
Výjimečně rigidní jedinci (pro něž bude nově zvolená konvence TČ příliš „jiná“) nemusí zoufat – všechny vzorce a ilustrační scénáře si mohou bez obav přepočítávat do „starých známých“ jednotek – na platnost fyzikálních zákonů to nebude mít vliv, matematické vzorce (a výpočty) však pro ně budou o něco komplikovanější.
3.2.1 OBJEKT
Objektem je předmět našeho zájmu, neb je součástí (fyzikálního) děje. Pojmy objekt a hmotný objekt považujme za rovnocenné. Pojmy objekt a těleso jsou taktéž zástupné.
Objekty neexistují osamoceně, předmětem našeho zájmu je proto vždy více objektů – objekt sám o sobě (bez kauzální vazby na jiné objekty) nemá fyzikální význam!
Objekty zaujímají rozdílnou vzájemnou polohu v prostoru a čase (časoprostoru), která je definovaná prostřednictvím měření délek a časů – žádné dva objekty nemohou zaujímat stejné místo v časoprostoru.
Veškeré objekty jsou v neustálém pohybu!
3.2.2 HMOTA
Významový pojem „hmota“ je s ohledem na fyzikální význam tohoto slova v češtině poněkud matoucí, neboť slovně evokuje představu, že hmota je to, co je hmotné – má hmotnost. V tomto ohledu však jde o nepřesnou terminologii, neboť moderní fyzika „hmotou“ označuje obecně jakoukoliv její formu, tedy i hmotu s „nulovou klidovou hmotností“ či hypotetické formy hmoty čekající dosud na své potvrzení ať již ve formě částic, polí či vlnění. Mimo jiné čeká moderní fyzika na objasnění, jaká forma hmoty je zodpovědná za hmotnost (gravitační interakci).
V češtině jsme tedy pojem hmoty (o níž nevíme zdaleka vše) pojmenovali derivátem pojmu „hmotnost“ (o níž nevíme vůbec nic)!
Angličtina je v tomto ohledu ve výhodě, neboť oba pojmy rozlišuje (matter = hmota, mass = hmotnost).
Bez ohledu na matoucí češtinu – s ohledem na zvyklosti a srozumitelnost dalšího textu – ponechme i nadále pojem „hmota“ jako obecné označení veškeré „matérie“, která tvoří náš okolní svět a celý vesmír. Zjednodušeně budeme hmotu nadále dělit na látku a pole – viz schematicky a zjednodušeně:
HMOTA
• látka
• molekuly
• atomy
• hadrony (např. protony, neutrony, mezony) a jejich antičástice
• kvarky a antikvarky
• leptony (např. elektrony, miony, neutrina) a jejich antičástice (např. pozitron)
• pole
• fotony
• gluony
• wiony čili intermediální bosony
• gravitony (hypotetické – zatím nejsou experimentálně ověřeny)
Hmota (stejně jako objekty) neexistuje osamoceně v prázdném vesmíru. Hmota je v nám známém vesmíru (zdá se) rozložena homogenně a izotropně (v globální vesmírné perspektivě), lokálně se však slučuje do super-clusterů, galaktických grup, galaxií, hvězdných soustav, planet atd.
Hmota je vždy v pohybu!
Otázkou zůstává, vůči čemu se hmota pohybuje! TČ se vynasnaží odpovědět v dalších kapitolách.
Hmota, jež bude v dalších kapitolách předmětem našeho zájmu, je nejčastěji označována pojmem objekt či těleso.
3.2.2.1 ENERGIE (A HMOTNOST)
„Všechny částice jsou tvořeny ze stejné substance: Energie!“
Werner Heisenberg
V oblasti energie, hmotnosti, gravitace, tíhy, setrvačnosti, kilogramu a joulu je pojmosloví ještě více komplikované! V tomto ohledu již musíme nutně zavést smysluplnější pořádek – nemůžeme nadále žít v pojmovém chaosu a setrvávat v něm. Není možné používat několik pojmů pro jeden fyzikální fenomén.
Hmotností historicky označujeme množství hmoty, které lze měřit buď jako míru setrvačných, anebo gravitačních účinků hmoty. Roztlačit těžší automobil si žádá více úsilí (setrvačná hmotnost ≈ inertial mass), vyzvednout těžší předmět do výšky taktéž vyžaduje větší námahu (gravitační hmotnost ≈ gravitational mass). Poznatky dávných velikánů fyziky i experimenty přitom potvrzují, že oba projevy hmotnosti jsou ekvivalentní!
Navíc občas věc terminologicky komplikujeme tím, že gravitační hmotnost pojmenováváme termínem tíhová hmotnost. Tíha je pro 99 % populace (a to i v anglicky mluvících zemích) totiž synonymem pro hmotnost s tím, že se „samozřejmě“ udává v kilogramech. Skutečnost, že tíha je silou (a vyjadřuje se v newtonech), občas uniká i fyzikům – etymologie jazyka je neúprosná.
Celá věc se navíc zkomplikovala, když vyšlo najevo, že i pojmy hmotnost a energie jsou ekvivalentní E = mc2. Přestože jsme se tento fakt dozvěděli před více než 100 lety – fyzika dodnes nezareagovala a schizofrenně používáme pro vyjádření množství hmoty oba pojmy (jak se kdy hodí).
Mezinárodní úřad pro míry a váhy (BIMP) této situaci apaticky přihlíží a čas od času aktualizuje systém soustavy jednotek SI – vždy však tak, aby byla schizofrenie hmotnosti a energie zachována.
A aby byla situace ještě nepřehlednější – jednotkou hmotnosti v soustavě jednotek SI zůstává i nadále kilogram (nikoliv gram), takže hmotnost jako jediná má v základní soustavě jednotek SI předponu (kilo)!
V takovémto pojmovém zmatku nelze smysluplně poznávat fyziku. Proto si celou situaci významně zjednodušíme:
Následně budeme používat jeden jediný pojem pro množství hmoty a energie:
Hmota je tvořena energií a hmotnost je jejím ekvivalentem. A protože si v dalších kapitolách budeme chtít zjednodušit situaci – rychlost budeme vyjadřovat v jednotkových bezrozměrných hodnotách, kde c = 1, známý vztah E = mc2 se v našem případě zjednoduší na E=m. Ekvivalentnost hmotnosti a energie tak bude zcela zřejmá!
Množství hmoty (respektive množství energie) budeme nadále definovat primárně pojmem energie, jednotkou volíme kilogram (kg).
V závěru knihy zvolíme (kvůli finálnímu zjednodušení) zcela novou jednotku hmoty spacegram (sg).
Je velikou otázkou, co je to vlastně energie.
Učebnice fyziky zpravidla definují energii jako schopnost konat práci (či něco podobného) – což nás vzápětí navede do bludného kruhu otázek (co je to práce?) a nejasných odpovědí. S maximální snahou o prozíravost definujme energii (kromě míry množství hmoty) jako:
Energie je schopnost měnit pohybový stav hmoty.
V dalších kapitolách budeme energii vyjadřovat v joulech jen zcela výjimečně (pro srozumitelnost s ohledem na „tradici“). Stejně tak pojem hmotnost budeme používat zřídka – je zcela zbytečný, respektive je synonymem pojmu energie.
Vnímáme-li hmotnost jako ekvivalent energie, pak je zřejmé, proč objekt uvedený do pohybu musí být hmotnější (byť při malých rychlostech je nárůst nepatrný) – kinetická energie (Ek) přenesená na objekt má svoji hmotnost a o tuto hmotnost musí být objekt následně hmotnější (hybatel naopak stejnou hmotnost ztratí), protože Zákon zachování energie je pro nás zákonem stěžejním.
Onu počáteční hmotu objektu (před udělením kinetické energie ≈ před udělením pohybu) budeme označovat jako primární energie (E0). Pojem „klidová hmotnost (m0)“ je zvolen tradiční fyzikou nevhodně – je matoucí a zastírá skutečnost, že jakákoliv hmota je vždy v pohybu.
Svět bude pro nás všechny o hodně jednodušší, když přijmeme terminologii TČ a začneme používat „hybridní“ pojem energie, jejíž jednotkou bude kilogram!
veličina:energie
značení:E
jednotka:kilogram (kg)
přepočet:1 kg ≐ 9·1016 J
V závěrečných kapitolách dokonce zavedeme (z důvodů finálního zjednodušení) zcela novou jednotku energie, kterou „pracovně“ nazveme spacegram:
veličina:energie
značení:E
jednotka:spacegram (sg)
přepočet:1 sg = c3/(4πG) kg ≐ 3,2·1034 kg ≐ 2,9·1051 J
Vysvětlíme později – nechte se překvapit!
3.2.2.2 HMOTNÝ STŘED
Hmotný střed definujeme jako prostorovou polohu, vůči níž je rozložení energie (hmoty) lokálního uskupení objektů prostorově symetrické.
Ani v této oblasti nemá fyzika zcela jasno:
Pojmem „barycentrum“ nazýváme „hmotný střed“ nebeských těles. Často bývá používán i pojem „těžiště“, avšak nevhodně, neboť „tíží“ označujeme ve fyzice pouze gravitační sílu (jež je lokálně závislá – na Měsíci, například, je oproti Zemi pouze šestinová).
TČ proto bude používat termín „hmotný střed“ (či výjimečně pojem „barycentrum“), pojem „těžiště“ pouze v nadneseném slova smyslu.
3.2.3 ČASOPROSTOR (PROSTOR)
Časoprostor je 4D prostředí, v němž vše (lidé, věci, vesmír) existuje.
Žijeme v prostředí, které tvoří 4 na sebe navzájem kolmé roviny – 3 prostorové a 1 časová, přičemž ve třech prostorových rovinách se lze pohybovat libovolným směrem a čas „plyne“ ve čtvrté rovině jednosměrně „rychlostí“, která se historicky označuje jako „rychlost světla“. Fakticky však – čas definuje kauzalitu a pořadí událostí!
Časoprostor je vyjádřen specifickou pravoúhlou geometrií 4D prostředí – vyjadřující duální jednotu délkových a časových rozměrů našeho světa a celého vesmíru.
Časoprostor je v pojmovém smyslu reálného světa Euklidovským prostorem. Zjednodušeně řečeno – na časoprostoru není nic zakřiveného: Rovnoběžky zůstávají rovnoběžkami a součet úhlů v trojúhelníku dává 180° – na Pythagorovu větu se můžeme spolehnout!
Téměř všichni jsme již v minulosti zaznamenali existenci pojmů časoprostor či prostoročas. Není však třeba tyto složené pojmy používat vždy – pojem „prostor“ vždy měl a má sémanticky délkový i časový kontext (metrem měříme prostor pro stavbu domu, pohledem do diáře prostor pro dvouhodinovou schůzku).
Pojmy prostor, prostoročas i časoprostor tudíž považujme za rovnocenné, pakliže slovní kontext nespecifikuje něco jiného!
V češtině je opět nutné udělat „pořádek“ v terminologii – pojem „délka“ totiž často používáme nejen ve smyslu délkových vzdáleností (měříme metrem), ale i nekorektně ve smyslu „délky“ trvání časového intervalu (měříme hodinami).
Je proto nutné korektně definovat pojmy délka a čas – jakožto dvě provázané entity prostoru (časoprostoru):
3.2.3.1 DÉLKOVÁ VZDÁLENOST (DÉLKA)
Délkou měříme délkovou vzdálenost (odlehlost) vzájemné polohy objektů v prostoru a rozměry objektů.
U objektů měříme dle uvedené definice i tvary objektů a jejich rozměry – v rámci třech rozměrů „tradičního“ 3D prostoru.
Délku vyjadřujeme v sekundách! Klasická fyzika vyjadřuje délku zpravidla v metrech, ale je výhodnější ji vyjadřovat poměrem k délce, kterou urazí světlo za sekundu (3·108 m) – bude objasněno v dalších kapitolách.
veličina:délka
značení:l (či „s“ ve smyslu dráhy)
jednotka:sekunda (s)
přepočet:1 s ≐ 3·108 m
3.2.3.2 ČASOVÁ VZDÁLENOST (ČAS)
Je primární snahou TČ pochopit a definovat čas – alespoň rámcově. V tuto chvíli bude stačit, když definujeme:
Časem měříme časovou vzdálenost (odlehlost) vzájemné polohy objektů v prostoru a trvání dějů.
Zatímco délková rozlehlost našeho světa sestává z 3 rozměrů (3D), čas je velmi specifickou „dimenzí“ – je jednorozměrný (1D) a jednosměrný (záporné hodnoty, respektive „obrácená“ orientace času postrádají fyzikální interpretační smysl).
Čas ve výsledku definuje kauzální pořadí dějů sledovaných objektů – jednosměrná „orientace“ času rozlišuje příčinu a následek všech dějů ve vesmíru!
Čas vyjadřujeme (tradičně) v sekundách.
veličina:čas
značení:t
jednotka:sekunda (s)
3.2.4 POHYB
Pohyb znamená změnu vzájemné polohy objektů v prostoru, kdy se mění délkové a časové vzdálenosti těchto objektů.
Pohyb není relativní, nýbrž je absolutní, a to primárně vůči společnému hmotnému středu lokálního uskupení objektů v prostoru. Pro jednotlivé objekty hmotného uskupení lze objektivně určit, který objekt má pohybu více a který méně. Bude vysvětleno v dalších kapitolách.
Veškeré objekty jsou v neustálém pohybu!
3.2.4.1 HYBNOST
Hybnost je souhrnnou mírou pohybu – jíž se projevuje primární zákonitost pohybu hmoty – zákon symetrického pohybu objektů vůči svému hmotnému středu.
p = E v
veličina:hybnost
značení:p
jednotka:kilogram (kg), eventuálně spacegram (sg)
Bude vysvětleno později.
3.2.4.2 RYCHLOST
Rychlost je jednotkovou mírou pohybu (na jednotku hmoty) – vyjadřuje míru změny vzájemné polohy objektů v prostoru – a je určena poměrem změny délky (délková změna vzájemné polohy objektů) ke změně času (časová změna vzájemné polohy objektů).
Z matematického pohledu je rychlost derivací délky podle času.
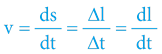
Rychlost je bezrozměrná veličina, neboť sekunda/sekunda = 1.
Sledujeme-li objekt pohybující se rychlostí světla (c), pak se objekt pohybuje jednotkovou rychlostí (v=1).
Analogicky jako pohyb – je rychlost veličinou absolutní, a to vůči společnému hmotnému středu lokálního uskupení objektů v prostoru. Pro pohyb objektů vůči sobě navzájem lze vždy objektivně určit, který objekt má větší rychlost a který menší. Bude vysvětleno v dalších kapitolách.
veličina:rychlost
značení:v
jednotka:(1)
přepočet:c = 1 ≐ 3·108 m/s
3.2.4.3 ČASOPROSTOROVÝ ÚHEL
Časoprostorový úhel je univerzální jednotkovou mírou pohybu (na jednotku hmoty), neboť geometricky vyjadřuje míru pohybu v časoprostoru, respektive mix délky (dráhy) a času (trvání) na celkovém pohybu v časoprostoru.
Časoprostorový úhel je (na rozdíl od rychlosti) univerzální mírou pohybu, která determinuje ostatní charakteristiky pohybu v časoprostoru – časové, rychlostní a energetické (hmotnostní) poměry.
veličina:časoprostorový úhel
značení:α
jednotka:radiány (rad)
přepočet:π/2 rad = 90°
Zatímco v běžném životě se používají pro označení úhlů především stupně (pravý úhel = 90°), věda preferuje radiány (pravý úhel = π/2 ≈ 1,5708).
Radiány jsou „přirozenou“ úhlovou jednotkou – protože hodnota úhlu v radiánech přímo vyjadřuje obvod kruhové výseče úhlem vytyčeným:
Používáme-li radiány v jednotkové kružnici, vyjadřuje hodnota radiánů přímo i délku obvodu kruhové výseče úhlem definované a všechny poměry délek v diagramu tak jsou proporcionálně korektní!
Teprve (a pouze) když udáváme hodnotu úhlů v radiánech – nacházíme v trigonometrických funkcích jejich „vnitřní krásu“ a hlubší smysl Euklidovské geometrie.
Bude vysvětleno později.
3.2.5 GRAVITAČNÍ POTENCIÁL
V tradiční fyzice definuje gravitační potenciál potenciální energii tělesa o jednotkové hmotnosti v gravitačním poli ostatních těles; jednotkou je J/kg a vypočítává se dle vztahu:
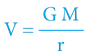
Budeme-li v této knize v dalších kapitolách poukazovat na „klasické“ fyzikální myšlení – budeme používat tento „tradiční“ vztah.
V rámci TČ (a její matematiky) tedy budeme gravitační potenciál vyjadřovat v kladných hodnotách (tradiční fyzika definuje gravitační potenciál jako záporný) a v závěrečných kapitolách zohledníme i nově definovanou jednotku energie (spacegram). Finálně tedy bude platit vztah:
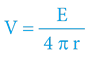
veličina:gravitační potenciál
značení:V
jednotka:bezrozměrná (1)
Nově definovaný gravitační potenciál vyjadřuje kinetický (pohybový) přírůstek energie, respektive přírůstek energie (hmoty) Ek/E0 „padajícího“ objektu v gravitačním poli. Jde o bezrozměrnou veličinu!
Zatímco moderní fyzika s oblibou označuje za ekvivalentní veličiny, které fakticky ekvivalentní nejsou (gravitace a zrychlení), jindy odmítá sloučit veličiny, které naopak ekvivalentní jsou (hmotnost a energie).
To je důvodem, proč se liší hodnota gravitačního potenciálu spočtená v „klasických“ jednotkách od hodnoty definované dle TČ – tradiční fyzice tudíž vychází gravitační potenciál numericky 9·1016násobně (c2) vyšší.
Proč je v tradiční fyzice gravitační potenciál záporný?
Fyzika tím reaguje na skutečnost, že nikdo (ani TČ) příliš netušíme, kdo v případě gravitace „platí účet za energii“. Kilogramový etalon má při dopadu na planetu Zemi o něco vyšší energii, tedy hmotu, tedy hmotnost. Stejně tak fotonům se mění na cestě vesmírem jejich hmota, respektive energie, respektive frekvence záření. A protože věda se zatím nehodlá smířit s myšlenkou, že energii získávají objekty prostřednictvím „prázdného“ vakua, „řešením“ je záporné znaménko gravitačního potenciálu, respektive „potenciální energie“.
Faktické řešení „problému“ však tradiční konvence nenabízí a fyzikálním vztahům ono „minus“ nesluší a působí zmatek v hlavách poznání chtivých čtenářů.
Pro přehlednost a smysluplnost bude proto TČ vyjadřovat gravitační potenciál (V) v kladných hodnotách.
Bude vysvětleno později.
3.2.6 DĚJ
Děj (fyzikální děj) znamená pohyb objektů. Pohyb se vždy týká více objektů – děj se proto nemůže týkat pouze jednoho samostatného objektu. Veškeré objekty jsou v neustálém pohybu!
Z výšeuvedených definic plyne, že děj objektů v prostoru je vždy popsán změnou délkových a časových vzdáleností (trvání), respektive rychlostí, respektive časoprostorovým úhlem objektů, respektive hybností.
3.2.7 UDÁLOST
Událost je informace o (fyzikálním) ději, respektive informace o pohybu objektů.
3.2.8 POJMOVÁ MAPA
Systém a definici veličin, značení a jednotky v rámci TČ přehledně představí následující diagram:
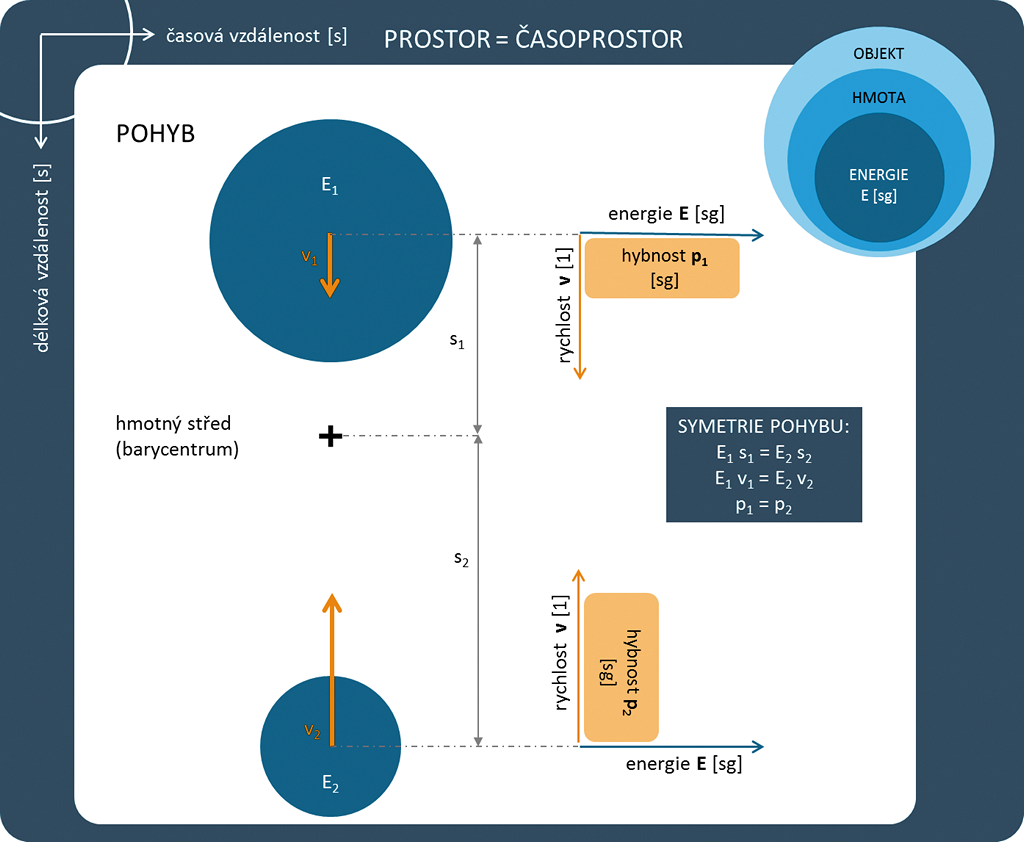
Obrázek 86:
Pojmová mapa TČ.
Na výšeuvedeném diagramu může leccos připadat čtenáři nesrozumitelné, ale v dalších kapitolách bude vše objasněno.
3.2.9 DĚJ Z INTERNÍHO A EXTERNÍHO POHLEDU
„Věci nejsou tím, čím se zdají být.“
autor nezjištěn
Vědci a badatelé mohou většinu fyzikálních dějů pouze pozorovat, jen některých dějů se můžeme přímo účastnit – z důvodů biologických, technologických i fyziologických omezení lidstva a organismu člověka. Tento fakt občas fyziky mate, když své vlastní pozorování děje mylně interpretují jako děj samotný.
V případě pohybu vlaku můžeme být externím pozorovatelem děje i interním strojvedoucím sledujícím měřicí přístroje – obojí je možné. Nikoliv však vždy:
Můžeme se snažit externě pozorovat pohyb fotonů či elementárních částic v urychlovači, avšak nemůžeme sami měřit fyzikální parametry takového děje z interní pozice takovýchto částic – zkoumaná věc je příliš malá a příliš rychlá. Můžeme externě pozorovat světlo ze vzdálených galaxií, ale nemůžeme interně provádět (z pozice světla) měření uvnitř takovýchto galaxií – zkoumaná věc je příliš daleko (v prostorovém i časovém významu) a neumíme vědce „transformovat“ do paprsku světla.
Abychom nezaměňovali oba světy, označujme veličiny z pohledu externího pozorovatele indexem „e“ a veličiny z pohledu interního účastníka indexem „i“.
Uvědomme si přitom, že pouze „i“ veličiny jsou ze své podstaty „reálné“ a z vědeckého pohledu ty nejlépe popisující skutečnost – jsou výsledkem bytí součástí děje.
Ať již jde o vědce fyzika, lékaře či psychologa – prožitek „na vlastní kůži“ je vždy 100× cennější nežli sebelepší externí pozorování a následné „myšlenkové experimenty“.
Mohl by fyzioterapeut úspěšně zkoumat techniku plavání, kdyby sám nikdy neplaval ve vodě? Cožpak není pro sexuologa důležité znát onen pocit sexuálního splynutí dvou osob? A proč tolik význačných lékařů provádělo pokusy s novými preparáty (či léčebnými postupy) primárně na sobě?
Chceme-li poznat pravdu – je velmi výhodné moci být interním účastníkem děje. Je to nejpřímější cesta k poznání, protože externí pozorování mohou být často ošidná. Sledovat dokument o lásce a prožívat lásku – přináší dvě velmi odlišné znalosti. Můžete celý život pečlivě studovat lyžaře a techniku lyžování, a přesto se to nejdůležitější dozvíte teprve tehdy, když se sami spustíte na lyžích ze svahu dolů. Analogicky totéž platí i o hudbě, farmakologii či létání.
Každý opravdový vědec by měl upřednostňovat „i“ experimenty. Moderní fyzika (částicová fyzika, astrofyzika, kosmologie, …) má bohužel jen velmi malé možnosti zkoumat podstatu světa z perspektivy interního pozorovatele. O to více by měla být při interpretaci svých vědeckých poznatků na pozoru! Externě pozorované „e“ informace jsou vždy pouze „zprostředkované“, a tím pádem mohou být i ošidné!

