Kdo hledá – najde!
„Zkoumáme-li všechny velké pravdy, zjistíme nakonec, že jsou jednoduché a snadno pochopitelné. Pokud ne, nejde o velké pravdy.“
Napoleon Hill
Přiblížili jsme se závěru této knihy …
V předchozích kapitolách jsme společně hledali odpovědi na takové otázky, které nám ve škole nikdy úspěšně neobjasnili.
Pozorný čtenář jistě zaznamenal, že Teorie času je jen velmi málo „kompatibilní“ se současným mainstreamovým pohledem na fyzikální interpretaci času, související kinematiku, gravitaci a nebeskou mechaniku.
V předchozích kapitolách jsme formulovali některé alternativní (smysluplnější) fyzikální zákony i navrhli experimenty, které by mohly pomoci zvolit správnou cestu na rozcestí, před kterým fyzika již několik desetiletí bezmocně přešlapuje:
Relativismus má totiž (možná) i dnes své místo v bezobsažných filosofických debatách – v exaktních vědeckých oborech je však relativismus v roce 2016 neudržitelný a s ním i celá Teorie relativity!
V minulém století byla TR v některých ohledech užitečná … dnes je však „mentálním blokem“ a brzdou rozvoje obecné fyziky i astrofyziky – příliš relativizuje vědecké poznání světa, omezuje fyzikální myšlení a zatemňuje logické uvažování.
Vesmír je přitom kategorií objektivní, neomezenou a projasněnou zjištěním našich předků, že svět je poznatelný a každý vědecký objev nás vždy o trochu více přiblíží faktické realitě:
• Země objektivně obíhá kolem Slunce! Opačný scénář není „relativní“ – je mylný!
• Rychlost pohybu hmoty je principiálně nekonečná! Pilota dostatečně pokrokové kosmické lodi nebude nic „omezovat“ v překročení rychlosti 300 000 000 m/s! Fakt, že takovémuto pohybu naměříme (zpovzdálí) určitou limitní rychlost, je jen projevem existence času – jakožto 4. rozměru našeho časoprostoru.
• K vysvětlení pohybu všech nebeských těles si stačí „ujasnit“ zákony pohybu a gravitace. Temná hmota je nepotřebná!
Bez „omezujících“ postulátů TR bude zkoumání našeho světa o dost jednodušší, svobodnější a (mimo jiné) i „vnitřně krásnější“!
Vědecká činnost (a poznávání obecně) jsou úchvatné právě proto, že nemají hranic! Před každým z nás je i v roce 2016 nepřeberné množství záhad, které touží být objasněny. Jde o „nekonečný příběh“ – proces poznávání neskončil s Teorií relativity a nekončí ani s Teorií času.
Převezmeme-li štafetu od našich předků a budeme-li pokračovat v hledání odpovědí na zvídavé a dotěrné otázky – svět a vesmír nám odpoví.
A budou to odpovědi objektivní, nikoliv relativní – budou jasné a zřetelné, nikoliv temné či černé!
Věda není nic jiného nežli hledání odpovědí … a jednou z odpovědí je i ona omšelá pravda, že kdo hledá – najde!
KISS
Ve druhé kapitole jsme diskutovali (mimo jiné) i Princip logické úspornosti, jehož novodobou podobou je akronym KISS (Keep it short and simple) – výstižné vyjádření pravidla, že i věda by měla preferovat jednoduchá řešení před těmi složitými.
Jak si stojí Teorie času dle výšeuvedeného hlediska?
Představme si neutronovou hvězdu, jejíž gravitační potenciál je roven hodnotě 0,3.
Obě teorie se tentokráte shodnou na existenci neutronových hvězd (na rozdíl od kauzy Černých děr) i na mohutnosti gravitačního potenciálu takovýchto „extrémistických“ vesmírných objektů (byť tradiční fyzika používá méně vhodný systém jednotek a k hodnotě 0,3 se dopočítá teprve tehdy, když svůj gravitační potenciál vydělí konstantou c2).
Nakolik složité je určit „kosmickou“ (únikovou/dopadovou) rychlost na povrchu takové neutronové hvězdy? Kterak bude zpomalen čas dopadajícího objektu?
Jak moc komplikované uvažování potřebujeme k nalezení řešení? Jak moc robustní matematiku?? Jak moc zakřivenou či imaginární metriku???
Buď se můžeme snažit použít Teorii relativity – vyjít z několika diferenciálních rovnic, časem dospět ke Schwarzschildovu řešení a pak vzít do ruky kalkulačku, abychom ve výsledku dospěli k nekorektnímu výsledku … anebo na stůl položíme čistý list papíru, pravítko a kružítko – a provedeme pár jednoduchých tahů:

Narýsujeme úsečku dlouhou 1,3 (třeba 13 cm) …

… a bodem „1“ vedeme kružnici.

Zkonstruujeme tečnu ke kružnici …
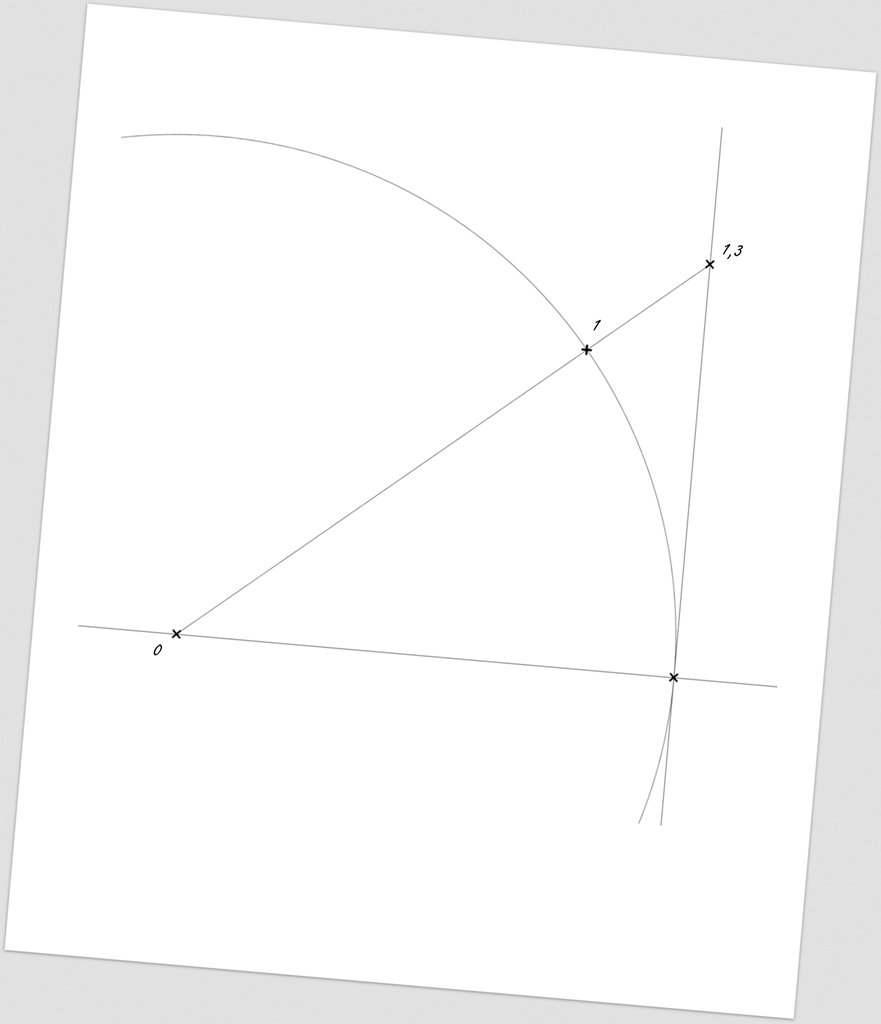
… a k této tečně následně kolmici (procházející středem kružnice) – čímž získáme časovou osu „x“.
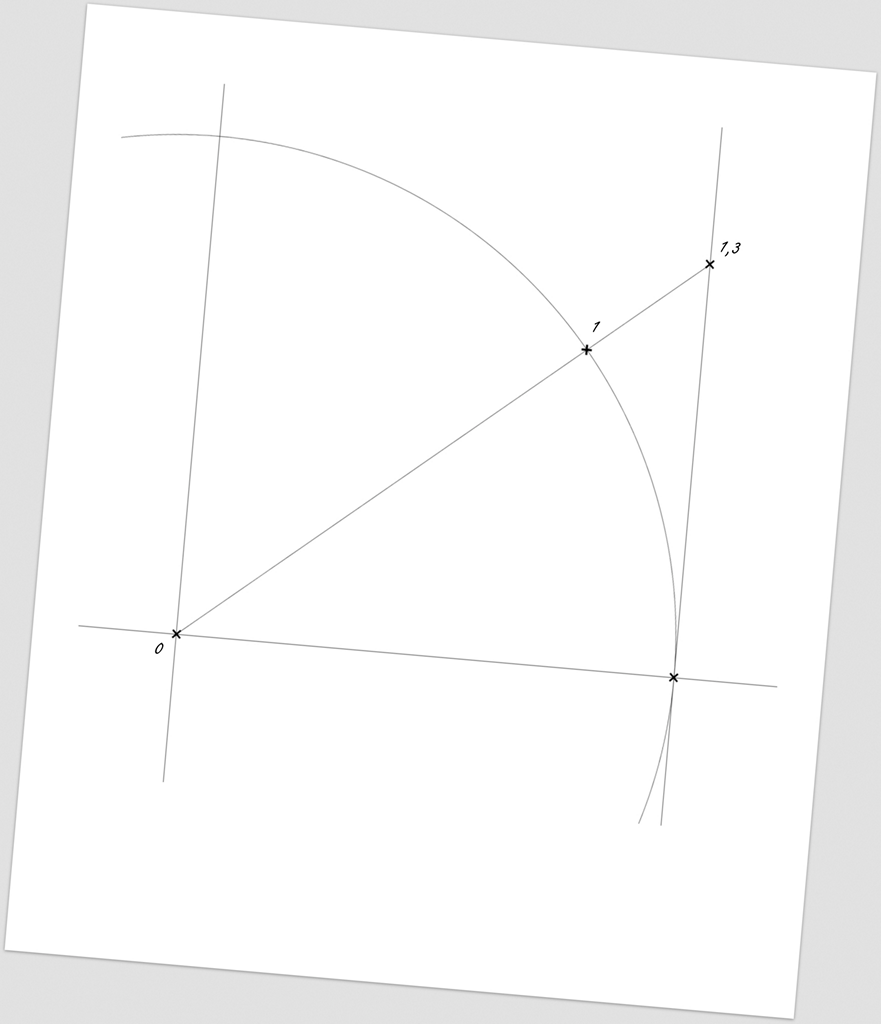
Další kolmice (vedená středem kružnice) nám dokončí konstrukci časoprostorové kružnice – čímž získáme rychlostní osu „y“.
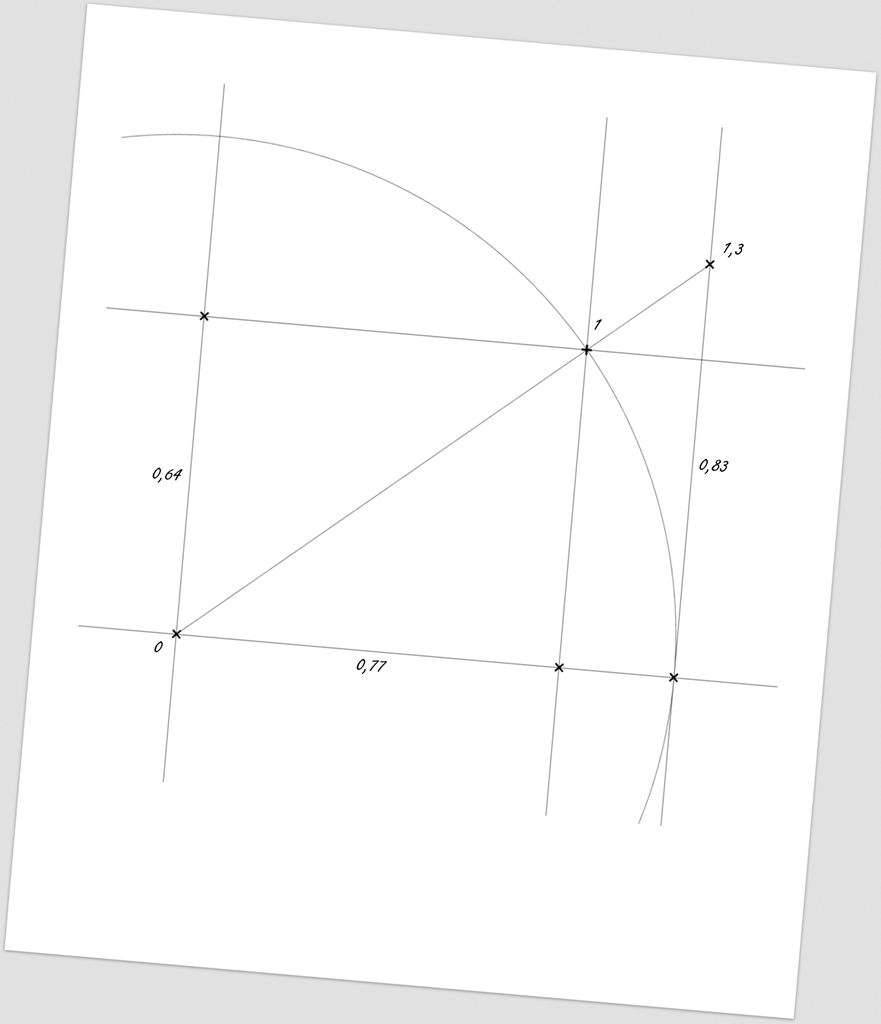
Bodem „1“ vedeme rovnoběžky k oběma osám – čímž získáme odpovědi na všechny otázky ohledně neutronových hvězd.
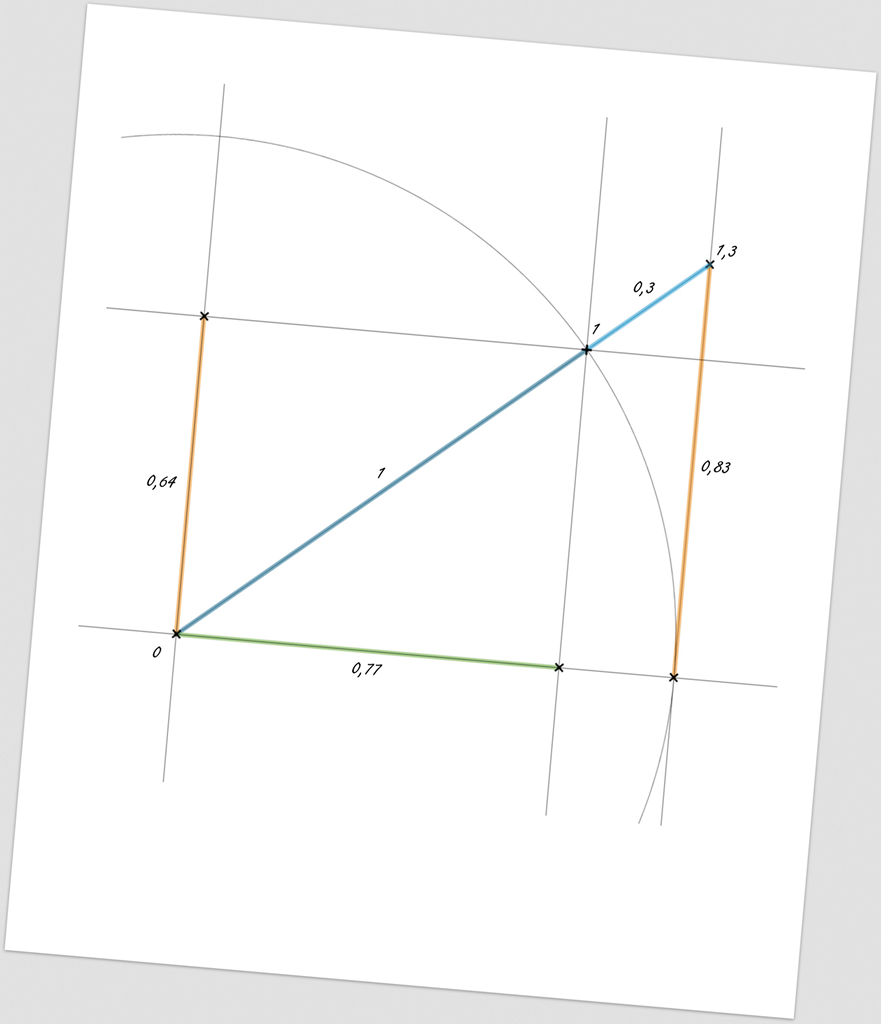
Obrázek 152:
Odměřené hodnoty můžeme i barevně zvýraznit.
Teorie času „umí“ každou situaci snadno narýsovat – umí vše vyřešit geometricky – nic víc než kružítko a pravítko není potřeba!
V našem konkrétním případě lze z nákresu hravě určit, že „kosmická“ (úniková/dopadová) rychlost bude 0,64 (1,92·108 m/s) optikou externího pozorovatele; 0,83 (2,49·108 m/s) optikou interního pozorovatele a dilatace/kontrakce času bude 1,3/0,77 v závislosti na tom, kdo činí ono časové porovnání (interně/externě).
Na papíře vyřešíme celou úlohu s přesností na jedno desetinné místo, v kreslícím programu počítače s přesností na 3 desetinná místa, a když budeme vše „kreslit“ s použitím softwaru Geogebra, tak třeba i na 15 desetinných míst!
Především ve třetí kapitole této knihy se mohlo čtenáři chvílemi zdát, že matematika Teorie času není až tak jednoduchá, jak jsme slibovali v úvodu knihy – všude se objevovala spousta mocnin a odmocnin – velmi časté byly funkce sinus, cosinus, tangens, secans i exsecans. Ano – to vše je nutné přiznat …
… zároveň je ale nutné dodat, že 99 % všech těchto matematických „nepříjemností“ reprezentuje matematické vyjádření skutečnosti, kterou jsme na předchozí stránce tak snadno „nakreslili“ – nic víc!
Všechny ty složitě vypadající matematické vzorce jsou pouhým „názvoslovím“ a „konstrukcí“, jak na kalkulačce spočítat to, co jsme si v této kapitole společně narýsovali – pouhá náhrada pravítka a kružítka – triviální matematika pravoúhlého trojúhelníku – bazální „opakování“ tisíce let starých „počtů“!
Na samém závěru této knihy proto přichází autorovo omluvné přiznání:
Ano – celá tato (tlustá) kniha je knihou o matematice „obyčejného“ pravoúhlého trojúhelníku … o nic víc nejde … pouze jsme se naučili matematicky spočítat situaci, kterou si každodenně rýsují děti na základních stupních škol do svých sešitů!
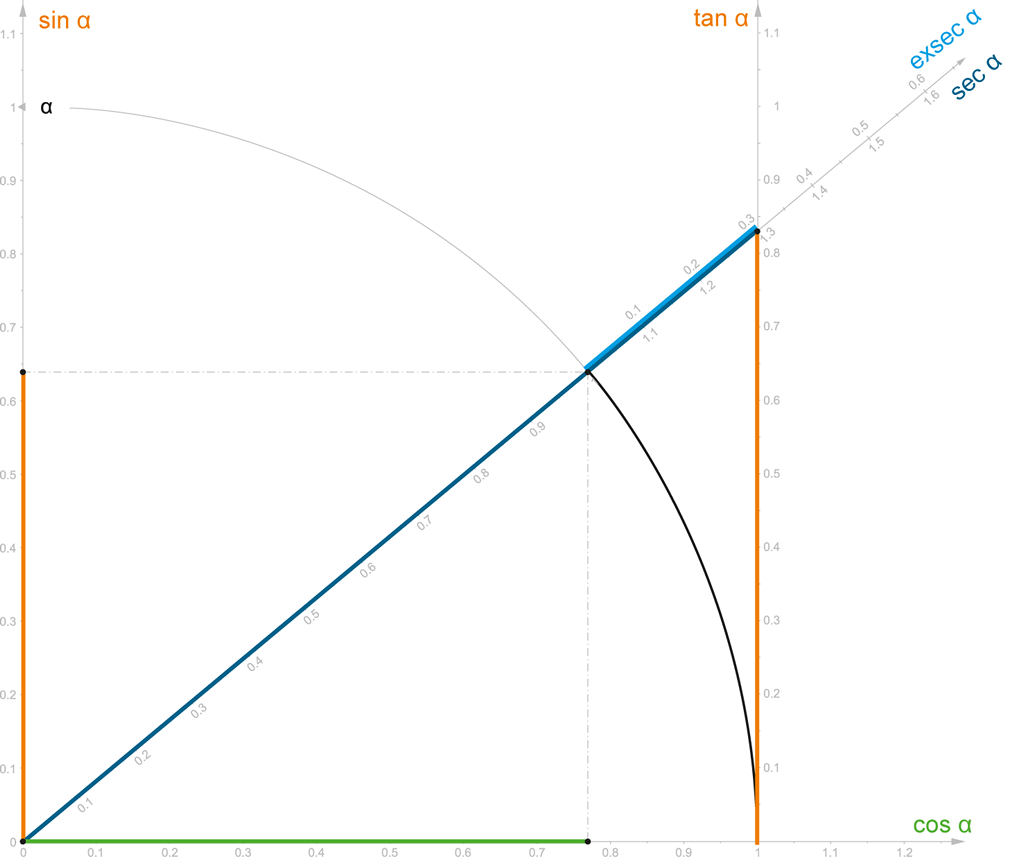
Obrázek 153:
Matematika pravoúhlého trojúhelníku.
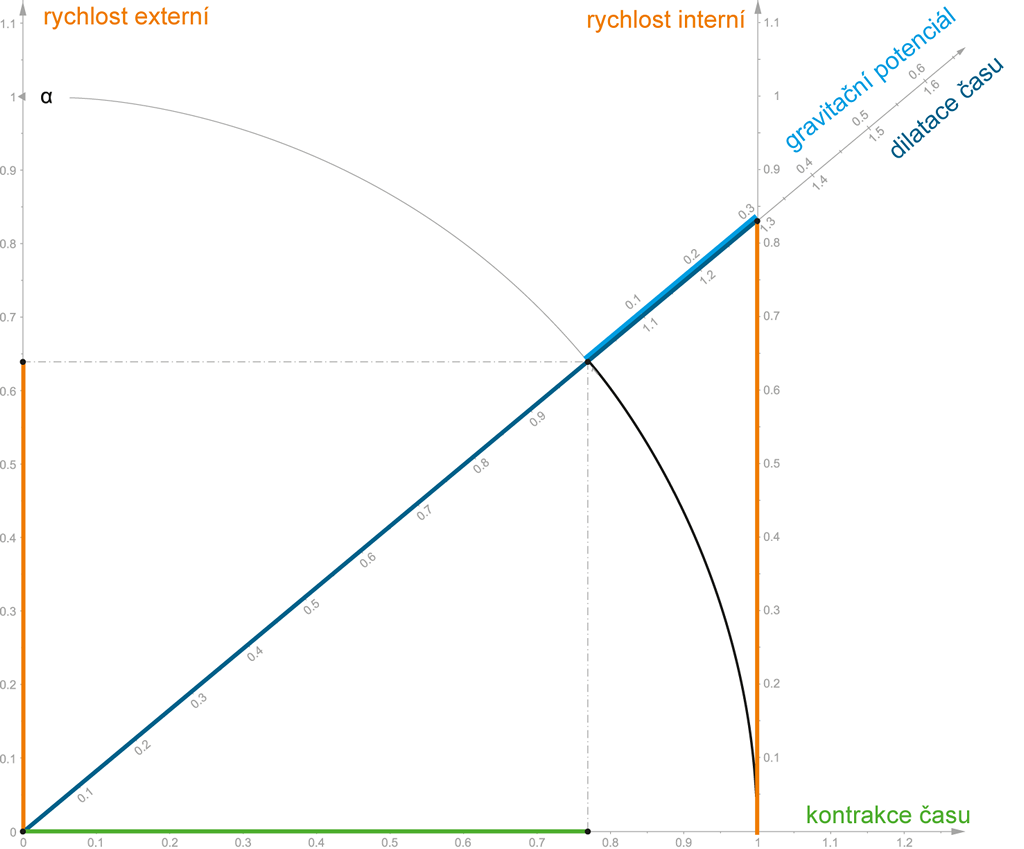
Obrázek 154:
Matematika pravoúhlého časoprostoru.
Je to skoro až trapné – fyzikálně i matematicky prostoduché – banální a triviální – žádná věda!
Teorie času má tudíž nulový potenciál nadchnout milovníky složité matematiky, obdivovatele nesrozumitelné terminologie či vzývatele „temných záhad“ …
… všichni ostatní se však mohou z jednoduchosti našeho (nepokřiveného) světa radovat!
KISS

