RESUMÉ K TEORII ČASU
„Všechny fyzikální teorie bez ohledu na své matematické vyjádření by měly být popsatelné natolik jednoduše, aby jim dokázalo porozumět i malé dítě.“
Albert Einstein
Čas je fenomén, který hraje v našem světě (i našich životech) jednu z nejdůležitějších rolí. Ve fyzikálním významu vstupuje čas naprosto do všech „dějů“. Přesto o čase víme tak málo!
TČ se pokouší poodhalit trochu více o podstatě a fungování času. A přestože čas zůstává i na konci této knihy velkou záhadou – víme o něm více nežli na jejím začátku:
Čas zůstává nehmatatelným a v mnoha ohledech imaginárním fenoménem. Má však svoje „místo“ v prostoru – spoluvytváří jej!
Čas má svůj vlastní prostorový rozměr – čas je 4. rozměrem našeho světa. A přestože pro mysl člověka jde o velmi těžko představitelnou provázanost 4D časoprostoru – matematicky jde o snadné řešení – platí zde Pythagorova věta, respektive základní trigonometrické funkce „jednotkové kružnice“ (založené na matematice pravoúhlého trojúhelníku). Nic víc není třeba!
TČ není teorií, kterou (pro systémovou složitost) může pochopit jen její tvůrce a (možná) několik vyvolených jedinců. Není třeba se bát soustavy složitých diferenciálních rovnic ani abstraktní matematiky v zakřivené metrice. Dobře zvládnutá matematika střední školy je pro pochopení TČ dostatečnou erudicí.
Matematickou jednoduchost však neberme jako hlavní hledisko – TČ klade primární důraz na jiné aspekty:
TČ je konzistentní ve své fyzikální podstatě!
TČ je prostá protimluvů a paradoxů. V TČ si jednotlivá tvrzení neprotiřečí. TČ vnímá přírodovědnou činnost jako snahu o pochopení objektivní pravdy a odmítá relativismus ve vědeckém myšlení. TČ vnímá svět (ve fyzikální i filosofické podstatě) jako poznatelný a přírodní vědy chápe jako hledání kauzálních zákonitostí. TČ deklaruje, že tvrzení „Slunce obíhá kolem Země“ a „Země obíhá kolem Slunce“ nejsou stejně validní – nejsou relativní!
Relativní nejsou ani vzdálenosti, délky a jiné rozměry našeho světa. Metrová tyč zůstává vždy metrovou tyčí a vzdálenost ze Země na Měsíc je stejná pro každého.
Za relativní považujeme především současnou úroveň „moderní“ astrofyziky!
Fyzikální podstata TČ spočívá ve formulaci 3 zákonů:
1. Vše existuje v Euklidovském čtyřrozměrném prostoru, který je tvořen třemi délkovými rozměry a jedním rozměrem časovým.
2. Množina lokálně izolovaných hmotných objektů se vždy pohybuje symetricky vůči svému hmotnému středu ve 4D Euklidovském prostoru tak, že se poloha toho středu v prostoru zachovává.
3. Hmota objektů není prostorově ohraničená – hmota každého objektu prostupuje ve formě gravitačního pole celým vesmírem.
Hmota generuje v prostoru gravitační potenciál, který klesá nepřímo úměrně vzdálenosti. Tento gravitační potenciál indukuje v okolních hmotných objektech kinetickou energii, respektive indukuje jejich pohyb. Tomuto jevu říkáme gravitace.
V důsledku gravitace se lokálně izolované objekty pohybují 4D Euklidovským prostorem symetricky vůči společnému hmotnému středu, který je zachováván.
 Společně tyto „zákony“ usilují o jednodušší a smysluplnější výklad našeho světa – našeho vesmíru – v duchu principu „logické úspornosti“.
Společně tyto „zákony“ usilují o jednodušší a smysluplnější výklad našeho světa – našeho vesmíru – v duchu principu „logické úspornosti“.
Zopakujme nyní to nejdůležitější, čím TČ mění pohled na současný stav fyzikálního myšlení:
• Hodinami měříme pořadí změn, které se v prostoru dějí – rozeznáváme tímto mechanismem kauzalitu, tedy příčinu a následek – říkáme tomu ČAS!
• Čas je též projevem mechanismu, jakým se prostorem šíří událost!
• Dvě tělesa nikdy nemohou sdílet společný prostor ani společný čas – vždy jsou oddělená v prostoru i čase – interakce mezi takovými tělesy proto bude vždy zatížena časovým „zpožděním“, které je úměrné jejich vzdálenosti. Čas tudíž není univerzální!
• Žijeme ve 4D časoprostoru, jehož čtvrtým rozměrem je čas! Časoprostor je Euklidovský (jeho jednotlivé rozměry jsou vzájemně kolmé), není jakkoliv zakřivený. Prostorovou vzdálenost – tedy délkovou i časovou vzdálenost vzájemné polohy objektů v časoprostoru měříme stejnou prostorovou jednotkou. V rámci TČ je touto jednotkou sekunda. Vzdálenost ze Země na Měsíc je tedy cca 1,25 sekundy.
• Rychlost je bezrozměrnou veličinou! Protože s/s = 1.
• Pohyb není relativní! Hmota se absolutně pohybuje vůči hmotnému středu lokálního uskupení objektů. Vždy tak lze exaktně určit, který objekt má pohybu více a který méně – pohyb lze objektivně kvantifikovat, a to nejen vůči hmotnému středu, ale i vůči jednotlivým objektům navzájem. Nástrojem pro objektivní kvantifikaci pohybů je geometrie (matematika) 4D časoprostoru.
• Pohyb je vždy symetrický – nikdy se tudíž netýká pouze jednoho objektu! Aby se hmota mohla pohybovat jedním směrem v prostoru, musí se jiná hmota pohybovat směrem opačným tak, aby celková hmota zůstala energeticky (hmotnostně) symetrická – vůči společnému hmotnému středu (barycentru).
• Pohyb objektů v časoprostoru popisuje geometricky i matematicky „jednotková“ časoprostorová kružnice, respektive trigonometrie. Univerzální míru pohybu definuje časoprostorový úhel, který objektivně rozlišuje mezi interními účastníky pohybového děje a externími pozorovateli – časoprostorový úhel tak mimo jiné definuje i dilataci času (či kontrakci času v obrácené perspektivě). Vše objektivně kvantifikují bazální trigonometrické funkce časoprostorového úhlu.
• Dilataci času spoluprovází kontrakce času! Záleží na tom, kdo činí ono časové porovnání. Interní účastník děje zaznamenává (v důsledku existence 4D časoprostoru) kontrakci svého času vůči externímu času spolu s růstem rychlosti, externí pozorovatel naměří naopak dilataci svého času vůči internímu času. Spolu s tím zaznamená interní účastník vyšší rychlost (teoreticky principálně neomezenou), zatímco externí účastník naměří zpomalování rychlosti, jež se limitně bude blížit „rychlosti času“ (v = c = 1).
• Rychlost pohybu hmoty tedy není principiálně omezená! To, že vnímáme rychlost šíření světla jako omezenou, je důsledek geometrie časoprostoru – optikou externího pozorovatele (který se neúčastní samotného pohybu). 4D časoprostor se externímu pozorovateli projevuje zdánlivou omezeností rychlosti pohybu.
Interně – pro samotný pohybující se objekt – však rychlost pohybu není jakkoliv omezena.
• Externí optikou je rychlost času (světla) 1! Tak to vždy bylo, je a bude – v celém vesmíru (c = 1).
• Hledisko interního a externího pohledu je ve výšeuvedeném smyslu pouze zjednodušující konvencí! S ohledem na symetričnost pohybů se vždy pohybují obě (všechny) strany děje. Pohyb „centrálního“ objektu ale můžeme často zanedbat pro jeho hmotnostní dominanci a přisoudit mu tak optiku externího pozorovatele.
V ostatních případech je nutné užít specifickou matematiku „sčítání“ rychlostí ve 4D časoprostoru.
• Problematika „sčítání“ rychlostí funguje dle dvou principiálně odlišných scénářů! Obě rozdílné fyzikální situace vyžadují rozdílnou matematiku.
• Kontrakce délek neexistuje! Prostorová délka, prostorové vzdálenosti i prostorové rozměry objektů nejsou relativní, ale absolutní (objektivní) kategorií. Vesmír se nezkracuje ve směru pohybu objektů, stejně tak se nemění délka objektů (ve směru pohybu). Vzdálenost ze Země na Měsíc (cca 1,25 s) je stejná pro každého!
• Jednoduchá matematika jednotkové kružnice definuje i výpočet kinetické a celkové energie pohybujícího se objektu! Objasňuje též ekvivalenci energie a hmotnosti.
• Hmotné objekty jsou tvořeny prostorově ohraničenou látkou a prostorově neohraničeným gravitačním polem!
• Vesmír není tvořen izolovanými hmotnými body ani hmotnými koulemi!
Vesmír je jedním uceleným, energeticky (a hmotnostně) vzájemně propojeným objektem – není prázdným prostorem, v němž se pohybuje nespočet ohraničených hmotných objektů!
• Vakuum není prázdné – vakuum je dalším skupenstvím hmoty! V každém místě vesmírného vakua je přítomno gravitační pole, jehož potenciál definuje pohyb ostatní hmoty. Toto gravitační pole má svoji energii, tedy i hmotnost!
• Energetická hustota současného vesmíru definuje odpor proti změně pohybového stavu – definuje setrvačnost – definuje energii (a tedy i hmotnost) všech objektů ve vesmíru! Globální (souhrnná) úroveň gravitačního potenciálu tak definuje primární energii (a hmotnost) objektů.
• Gravitace je projevem Zákona symetrického pohybu ve 4D prostoru za situace, kdy hmotné objekty nejsou prostorově ohraničené, jejich energie (hmotnost) sahá do nekonečna (gravitační potenciál klesá nepřímo se vzdáleností) a zároveň je tato energie sdílena ostatními hmotnými objekty!
• Hmota generuje v okolním prostoru gravitační pole, jehož potenciál klesá nepřímo úměrně vzdálenosti – působí do nekonečna (byť s klesající intenzitou). Takový gravitační potenciál zpětnou vazbou působí na všechnu ostatní hmotu ve vesmíru (nejen na látku) tím, že oné okolní hmotě „indukuje“ kinetickou energii (a tedy i hmotnost)! A právě tomuto jevu říkáme „gravitace“.
• Vlivem gravitace se hmota ve vesmíru shlukuje do lokálního uskupení objektů, jež (dle výšeuvedeného principu) vytváří lokální radiální gravitační potenciál, který je přímo úměrný energii onoho hmotného uskupení a nepřímo úměrný vzdálenosti od barycentra hmotného uskupení. Takto se formují galaxie, hvězdy, planety a další formy „látkových“ objektů.
• Rozdílné hladiny tohoto lokálního (radiálního) potenciálu indukují kinetickou energii – indukují pohyb okolních objektů, respektive definují exsekantu jejich časoprostorového úhlu, respektive rychlost jejich pohybu vůči barycentru hmotného uskupení objektů (ať již pohyb měříme optikou pohybujícího se objektu, anebo optikou nehybného „externího“ barycentra – vzhledem k Zákonu 4D prostoru).
Toto tvrzení se vztahuje na „běžné“ hmotné objekty mající „látkový“ charakter. Elektromagnetické záření (světlo) podléhá jiné matematice (exponenciála namísto exsekanty), nicméně opět ji určuje gravitační potenciál.
• Gravitační potenciál je tedy souhrnná veličina – přímo kvantifikující kinetický přírůstek energie vůči prvotní energii tělesa, jež se pohybuje mezi jednotlivými hladinami s rozdílnou intenzitou gravitačního pole. Jde o bezrozměrnou veličinu!
• Celkový gravitační potenciál tak přímo definuje (mimo jiné) i 2. kosmickou rychlost, respektive časoprostorový úhel pohybu, který je nutný k trvalému vymanění se z gravitačního vlivu daného objektu – obrácenou perspektivou definuje míru pohybu při dopadu tělesa „z nekonečné výšky“.
• Lokální distribuce hmoty v „blízkém“ vesmíru tedy určuje trajektorii a rychlost pohybu „látkových“ těles (vůči lokálnímu barycentru), jakožto i změny v jejich celkové energii (hmotnosti). Stejně tak – lokální hmotná uskupení zakřivují trajektorii elektromagnetického záření a mění jeho energii (frekvenci).
• Fotony jsou kvanty „čisté“ (kinetické) energie, prostorem se fakticky (interně) pohybují nekonečnou rychlostí (jednotkovou rychlostí z externího pohledu). V jejich případě tudíž gravitační potenciál okolních těles nemění rychlost jejich pohybu, ale přímo ovlivňuje primární energii záření, respektive jeho frekvenci. Projevem tohoto fenoménu je Gravitační posuv (GRP, GMP):
• GRP či GMP je přímo definován exponenciálou gravitačního potenciálu. Inverzně mohou tuto závislost použít astrofyzikové – a dle naměřeného posuvu mohou určit hodnotu gravitačního potenciálu vzdáleného objektu, z něhož světelné záření pochází.
• V důsledku gravitace (a výšeuvedeného) je zřejmé, že jeden ze „základních“ fyzikálních teorémů je pouhým mylným předpokladem: Tělesa se „setrvačností“ (bez působení síly) nepohybují rovnoměrným přímočarým pohybem! …
• … a protože reálně je ve vesmíru hmotných objektů více nežli dva (a navíc nebeská tělesa nejsou nikdy zcela kulatá a homogenní) – nebeská tělesa se nepohybují ani po kuželosečkách!
• Tělesa se bez působení síly (setrvačností) pohybují daným prostorem po křivkách, jejichž trajektorie je definována lokálním gravitačním potenciálem všech okolních těles – a to tak, aby pozice hmotného středu (lokálního uskupení objektů) zůstala zachována!
• Gravitační konstanta G je nepotřebnou fyzikální konstantou. Vhodně zvolená „racionalizace“ fyzikálních jednotek pro délku a energii (hmotnost) gravitační konstantu zcela eliminuje!
• Pakliže jsme stanovili jednotkou prostorové vzdálenosti (délkové i časové) sekundu, je onou racionální jednotkou energie (hmoty) ekvivalent 3,2·1034 kg! V rámci TČ jsme tuto jednotku nazvali „pracovně“ spacegram (1 sg = 3,2·1034 kg).
Metr, kilogram či joul jsou stejně nepraktické jednotky jako například stupně (°) pro úhlovou míru – jsou nepřirozené a vzájemně nekompatibilní – v jejich důsledku narůstají fyzikální vzorce o zbytečné konstanty. Sekunda, radián a spacegram popisují náš vesmír mnohem jednodušší formou!
• Účinky gravitačního pole a zrychleného pohybu nejsou ekvivalentní! Je poměrně snadné rozlišit, zda výtah „stojí“ v gravitačním poli, anebo se pohybuje rovnoměrně zrychleným pohybem v pustém vesmíru. Olovnice či kyvadlo umí rozhodnout!
• Stav beztíže při pádu v gravitačním poli a při (hypotetické) absenci gravitace taktéž není ekvivalentní! V praxi umí oba stavy rozlišit setrvačník a slapové síly (mikrogravitace).
• Gravitační pole – samo o sobě – neovlivňuje tok času! Tok času je ovlivněn pouze pohybem.
• Veškeré údajné důkazy zakřivení časoprostoru dle TR jsou neprůkazné a nevěrohodné! Buď příliš zjednodušují reálnou fyzikální situaci (precese Merkurova perihelia), anebo manipulativně interpretují fakta (gravitační posuv, GPS, ohyb světla).
• Proklamované „důkazy“ zakřiveného časoprostoru jsou ve skutečnosti důkazem pokřiveného vnímání zákonů vesmírné mechaniky! Soudobá astrofyzika „věří“ na elipsy a heliocentrismus stejně dogmaticky, jako středověká věda věřila na geocentrismus a božskou dokonalost kružnic.
Realitou našeho světa je však symetričnost pohybů – žádná hmota proto nikdy nemůže být „v klidu“ – žádná hmota nemůže nehybně trůnit v centru hvězdných soustav (či galaxií).
• Naše Sluneční soustava není ani geocentrická, ani heliocentrická – je barycentrická! Vzhledem k pohybům Slunce (SIM), vzhledem ke všem zbývajícím objektům Sluneční soustavy (jež nikdy nejsou dokonalou homogenní koulí) – jsou kuželosečky (kružnice, elipsy, paraboly, hyperboly) vždy pouze přibližnou aproximací reálných orbit vesmírných těles. Faktické odchylky orbitálních trajektorií (od predikovaných kuželoseček) jsou tudíž vždy důsledkem naivity našeho fyzikálního uvažování, nikoliv zakřivení časoprostoru!
• Budoucí cestování lidstva ke hvězdám bude méně fantaskní, nežli předpovídá TR. Za délku jednoho lidského života NELZE cestovat k hranicím viditelného vesmíru.
• Černé díry neexistují!
• Temná hmota neexistuje!
• TR je nekonzistentní a v mnoha ohledech mylná! TR je „bipolární“ teorií, která sice parciálně přispěla k některým validním matematickým vztahům, jako celek je však nekorektní a zavádějící. Filosofický rozměr relativismu je navíc „brzdou“ dalšího rozvoje vědeckého myšlení (jakožto metody poznávání reálných zákonitostí přírody).
• Realita (veškerý svět kolem nás) potvrzuje platnost Euklidovského pravoúhlého světa a našeho pravoúhlého „prostoru“!
K novému (korektnějšímu) pohledu na náš svět a vesmír není třeba doktorátu z matematiky – téměř všechny situace lze snadno „narýsovat“, následně odměřit s pomocí kružítka a pravítka, anebo (lépe) – exaktně spočítat s pomocí bazálních matematických funkcí. Základní matematický aparát TČ je totiž až „neuvěřitelně“ triviální:
SYMETRIE POHYBU VŮČI HMOTNÉMU STŘEDU:
![]()
VZTAHY ČASOPROSTOROVÉ KRUŽNICE:
![]() externí rychlost
externí rychlost
![]() interní rychlost
interní rychlost
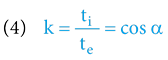 kontrakce času
kontrakce času
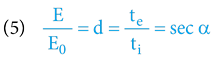 nárůst celkové energie; dilatace času
nárůst celkové energie; dilatace času
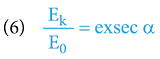 poměr kinetické energie
poměr kinetické energie
 externí čas rovnoměrně zrychleného pohybu
externí čas rovnoměrně zrychleného pohybu
„SČÍTÁNÍ“ RYCHLOSTÍ:
Objekty se vzdalují přímočaře od společného hmotného středu:


Objekty se pohybují kaskádovitě přímočaře:
![]()
![]()
GRAVITACE:
 gravitační potenciál
gravitační potenciál
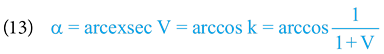 2. kosmická rychlost
2. kosmická rychlost
![]() gravitační posuv
gravitační posuv
Představme si, že na hranici naší SS, tedy ve vzdálenosti jednoho světelného roku 1 LY ≈ 9,5·1015 m, „upustíme“ směrem ke Slunci libovolné těleso a zároveň vyšleme i paprsek světla – obojí necháme volně „padat“ směrem ke Slunci. Jak se projeví gravitace Slunce při dopadu obou forem hmoty na jeho povrch?
• Začneme tím, že obecně dohledatelné údaje (rozměry, vzdálenosti a hmotnost Slunce) převedeme do racionálnějších jednotek TČ: Energie (hmota) Slunce E = 6,19·10‒5 sg, poloměr Slunce r1 = 2,32 s, vzdálenost Slunce od hranice SS r0 = 3,17·107 s.
• Spočítat následně gravitační potenciál na povrchu Slunce je triviální – viz vztah č. 12! Vyjde nám, že V = 2,12·10‒6; v daném případě se V ≈ ∆V, neboť gravitační potenciál Slunce je na okraji SS de facto nulový.
• Funkce exp (ex) gravitačního potenciálu nám následně (během jediné matematické operace) vypočte gravitační modrý posuv (GMP) paprsku světla při dopadu na povrch Slunce – viz vztah č. 14! Vyjde nám, že GMP = 1,000002123.
• Známe-li gravitační potenciál, známe zároveň i exsekantu časoprostorového úhlu. Funkci exsecans bohužel na kalkulačkách nenajdeme, nicméně ji snadno převedeme na funkci cosinus. Spolu s tím si (jaksi mimoděk) spočteme kontrakci času v okamžiku dopadu tělesa cos α = 1/(1 + V) = k. Vyjde nám, že cos α = 0,999997877.
• Hodnotu časoprostorového úhlu α následně snadno spočteme (během jediné matematické operace) pomocí inverzní funkce arccos – viz vztah č. 13! Vyjde nám, že α = 0,002060682 rad.
Známe-li časoprostorový úhel – vše zbývající vždy opět vyřeší jediná matematická operace:
• Externí rychlost dopadu tělesa nám spočte funkce sin – viz vztah č. 2! Vyjde nám, že ve = 0,002060681.
• Interní rychlost dopadu tělesa nám určí funkce tan – viz vztah č. 3! Vyjde nám, že vi = 0,002060685.
Stejně snadné to bude i v případě jakéhokoliv jiného objektu – v libovolné části vesmíru!
Nepotřebujete Riemannovskou geometrii, nemusíte řešit soustavy diferenciálních rovnic, můžete ignorovat „tenzorový počet“. Vše, co se snaží (velmi komplikovaně) kvantifikovat STR i OTR, dokážete spočítat „lusknutím prstu“ s použitím jediné matematické operace – stačí jakákoliv (i ta nejlevnější) „vědecká“ kalkulačka ze supermarketu.
Není to úchvatné?
Snadno si můžete ověřit, že zmíněný scénář generuje pro scénář naší SS následující výsledky:
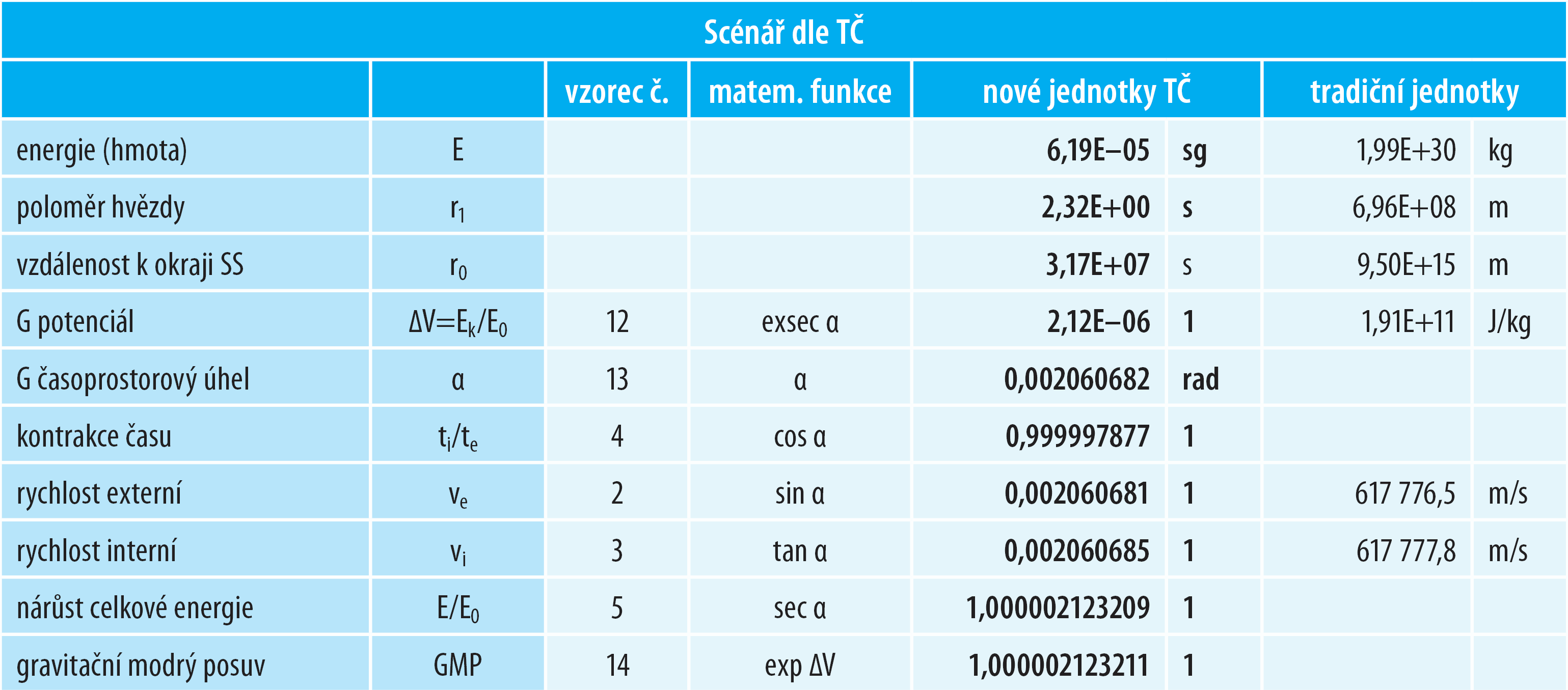
Tabulka 13: Volný pád ke Slunci z okraje naší galaxie
Výšeuvedená tabulka (matematické funkce i čísla v ní uvedené) nereprezentují nic jiného nežli bazální matematiku pravoúhlého trojúhelníku. Téměř veškerou problematiku gravitace tedy umíme řešit primárně díky Pythagorovi, Euklidovi, Archimedovi a myslitelům dávného Orientu – Aryabhata a Al-Birúní.
Pouze matematický aparát pro výpočet gravitačního posuvu frekvence světelného záření (exponenciální funkci) nám dal „až“ roku 1748 geniální Euler. S výjimkou GMP je tedy celá úloha snadno řešitelná i geometricky (s pomocí pravítka a kružítka) – jak si ukážeme později.
Geometrie časoprostoru … Dilatace času … Gravitační rudý posuv …
V uplynulém století byly tyto mysteriózní fyzikální fenomény opředené neproniknutelnou mlhou „relativismu“ a ujišťováním, že máte jen mizivou šanci narodit se jako génius, abyste tomu všemu směli porozumět.
Svět bychom si však neměli dělat složitějším, nežli je ve skutečnosti!
TČ v kostce:
• odmítnutí principu relativity;
• zavedení absolutního (objektivního) hlediska pohybu (který se nikdy netýká jen jednoho objektu), a to vůči hmotnému středu lokálního uskupení objektů;
• objekty se setrvačně nepohybují rovnoměrným přímočarým pohybem, ani po kuželosečkách – pohybují se takovou trajektorií, aby byl zachováván hmotný střed lokálního hmotného uskupení;
• a to vše se odehrává v Euklidovském (nezakřiveném) 4D časoprostoru našeho vesmíru;
• který je tvořen jediným společným, sdíleným hmotným uskupením, kde gravitační potenciál každého objektu (sahající do nekonečna) indukuje ostatním okolním objektům kinetickou energii (pohyb).
TČ akcentuje fakt, že téměř veškeré historické úspěchy lidstva v poznávání světa (detailní zmapování planety Země, určení vzdáleností a rozměrů nebeských těles, sestavení „mapy“ nám známého vesmíru, …) jsou založené na principech trigonometrie (matematika pravoúhlého trojúhelníku).
Úspěchy Euklidovské geometrie jsou nejen triumfem pravoúhlého vidění světa, ale i související matematiky – Pythagorovy věty a odvozených trigonometrických funkcí (sin, cos, tan, sec, …). Co jiného jsou druhé mocniny a odmocniny nežli matematickým vyjádřením poměrů v Euklidovském světě a pravoúhlém trojúhelníku?
![]() není ničím jiným nežli délkou přepony rovnoramenného pravoúhlého „jednotkového“ trojúhelníku.
není ničím jiným nežli délkou přepony rovnoramenného pravoúhlého „jednotkového“ trojúhelníku.
Mimo pravoúhlý (Euklidovský) prostor přestává reálná matematika existovat a stává se bezobsažnou hypotetickou vědou – pavědou!
Objekt sice může být zakřiven (například globus), prostor však nikoliv. Nepleťme si zakřivení objektů se zakřivením prostoru! Zakřivený časoprostor ponechme „na hraní“ filmovým tvůrcům, spisovatelům vědecko-fantastické literatury a rigidním obhájcům TR.
A raději si připomeňme ještě jednou:
Slunce není nehybným středem heliocentrické Sluneční soustavy! Hvězda zvaná Slunce vykonává celou polovinu veškerého pohybu v naší SS. Nehybný „centrální“ vesmírný objekt je nesmyslnou fyzikální kategorií!

